Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Wolak_2016,
   doi = {10.17512/jamcm.2016.1.19},
   url = {https://doi.org/10.17512/jamcm.2016.1.19},
   year = 2016,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {15},
   number = {1},
   pages = {191--196},
   author = {Wiktor Wolak and  Mirosław Roman Dudek and  Dinh Quang Ho and  Karol Marcjan},
   title = {Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2016.1.19
UR  - https://doi.org/10.17512/jamcm.2016.1.19
TI  - Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Wolak, Wiktor
AU  - Dudek, Mirosław Roman
AU  - Ho, Dinh Quang
AU  - Marcjan, Karol
PY  - 2016
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 191
EP  - 196
IS  - 1
VL  - 15
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Wolak, W., Dudek, M., Ho, D., & Marcjan, K. (2016). Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles. Journal of Applied Mathematics and Computational Mechanics, 15(1), 191-196. doi:10.17512/jamcm.2016.1.19

Wolak, W., Dudek, M., Ho, D. & Marcjan, K., 2016. Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles. Journal of Applied Mathematics and Computational Mechanics, 15(1), pp.191-196. Available at: https://doi.org/10.17512/jamcm.2016.1.19

[1]W. Wolak, M. Dudek, D. Ho and K. Marcjan, "Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 1, pp. 191-196, 2016.

Wolak, Wiktor, Mirosław Roman Dudek, Dinh Quang Ho, and Karol Marcjan. "Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles." Journal of Applied Mathematics and Computational Mechanics 15.1 (2016): 191-196. CrossRef. Web.

1. Wolak W, Dudek M, Ho D, Marcjan K. Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(1):191-196. Available from: https://doi.org/10.17512/jamcm.2016.1.19

Wolak, Wiktor, Mirosław Roman Dudek, Dinh Quang Ho, and Karol Marcjan. "Understanding of the role of pH in filling mezoporous silica with magnetic nanoparticles." Journal of Applied Mathematics and Computational Mechanics 15, no. 1 (2016): 191-196. doi:10.17512/jamcm.2016.1.19

UNDERSTANDING OF THE ROLE OF PH IN FILLING MESOPOROUS SILICA WITH MAGNETIC NANOPARTICLES

Wiktor Wolak ¹, Mirosław Roman Dudek ¹, Dinh Quang Ho ^1,2, Karol Marcjan ¹

¹ Institute of Physics, University of Zielona Gora
Zielona Góra, Poland
² Vinh University
Vinh city, Nghe An, Vietnam
20000621@stud.uz.zgora.pl, M.Dudek@if.uz.zgora.pl hodinhquangdhv@gmail.com, karol.marcjan@gmail.com

Abstract. Computer simulation study of filling pores of mesoporous silica with magnetic iron oxide nanoparticles which are diffusing towards the silica surface from a water solution with a given pH was presented. Three different values of the pH of the solution were under consideration, pH = 4, 7, and 10. The size of nanoparticles was of the order of magnitude of the nanopore diameter. It was observed that in the case of a low concentration of magnetic nanoparticles in the water solution the process of filling the silica pores weakly depends on the pH of the solution. The value of pH becomes only relevant for large concentration of magnetic nanoparticles. In the simulation, a 2-state Potts model was used for preparing the silica matrix. Diffusion of magnetic nanoparticles was restricted to lattice sites only.

Keywords: mesoporous silica, magnetic nanoparticles, point of zero charge

1. Introduction

Recently, an increasing number of engineering applications of magnetic nano-particles can be noted, especially those based on iron oxides which are non-toxic or where the toxicity is negligible. There are materials for medical applications like magnetic resonance [1] or drug release [2] but also new materials for industrial chemistry [3], or materials for environmental protection. In our recent papers [4, 5] we showed the special feature of iron oxide nanoparticles both experimentally and theoretically that when some amount of acid or base is added to an aqueous solution containing magnetic grains, then the solution close to the nanoparticles becomes, respectively, less acidic and less alkaline than it is expected. This property was suggested to be used in the design of new type of mortar with magnetic grains inside [5] achieving an increased compressive strength of mortar as well as its chemical protection against the acidic environment. In the following, we discuss the effect of the pH of water suspension of magnetic nanoparticles on filling the pores of the mesoporous silica. To this aim computer modeling methods have been used.

2. Preparing porous matrix

A series of models of porous glass were introduced which were studied with the help of computer simulation methods, like the molecular dynamics method presented in papers [6, 7]. In the following, we used the Metropolis Monte Carlo method, instead. To model porous glass, the 2-state Potts model on cubic lattice was chosen to simulate the phase separation of a binary mixture by analogy to a molecular dynamics approach presented in papers [6, 7]. The following interaction hamiltonian between two kinds of model atoms A and B of the binary mixture is assumed:

(1)

where lattice sites , are occupied by atom (A or B), the angular brackets denote summation over the nearest-neighbour lattice pairs. In the following, atoms A represent silica material and atoms B represent vacancies. Hamiltonian in Eq. (1) is the particular case of the hamiltonian which was introduced in paper [8] to model the sintering process in metal powders. We assume that and . Initially, atoms A and vacancies B are randomly placed in the sites of a cubic lattice with a given concentration of atoms A and of vacan- cies, and . During the computer simulation, atoms and vacancies which are located in the neighbouring lattice sites i, j can exchange according to Metropolis rule with a success rate equal to , where denotes the energy difference between the new and old lattice site configuration. In Figure 1, it has been shown the result of Monte Carlo simulations of a cube with dimension lattice sites in x, y, z direction. The periodic boundary condition was applied.

Fig. 1. Result of N = 600 MC steps of computer simulation of binary alloy of initially randomly distributed atoms A and B on cubic lattice. The parameters which have been chosen: , , , K, concentration of A atoms . Atoms A (in red) represent model of porous silica

3. Magnetic nanoparticles suspension

In the model, magnetic nanoparticles are represented by spheres of radius which can occupy cubic lattice sites. The cubic lattice is partitioned into two parts where the first one is represented by silica sites and the remaining sites represent a solution contacting the silica surface. Each sphere representing magnetic nano-particle possesses magnetic dipole moment and a point charge in its center. The value of charge is the same for each sphere. It represents the electrostatic charge acquired by iron oxide material when it is contacting a water solution with a given pH value. Then, there is electrostatic repulsion between spheres as well as magnetic attraction due to the magnetic dipolar interaction. The electrostatic part of the inter- action potential is the following:

(2)

where is the distance between the centers of mass of the nanoparticles located at sites and , represents permittivity, is the Debye length

(3)

denotes electron charge, is the Boltzmann constant, is the Avogadro number, represents ionic strength. It is assumed that the electrostatic surface potential of the nanoparticle can be approximated by Nernst potential, which depends on pH as follows [11]:

(4)

where is the gas constant, is the Faraday constant and PZC represents the point of zero charge. In the following, we have chosen PZC = 7.9 for magnetic nanoparticles and PZC = 2 for porous matrix representing silica. The surface charge density is expressed as the following:

(5)

and it is assumed that .

Magnetic interaction potential represents magnetic dipole-dipole interaction accord- ing to the formula:

(6)

where and represent magnetic moments of nanoparticles at site and , respectively. The interaction potentials are complemented by the Lennard-Jones interaction potential which represents the short-ranged Van der Waals interaction, respectively the magnetic nanoparticle-magnetic nanoparticle and magnetic nanoparticle-silica in the water solution. In general, the silica surface will acquire charge after contacting water solution with a given pH which is different from the value of . In this case, the electrostatic interaction potential in Eq. (2) is changed to the following one:

(7)

In the model, magnetic nanoparticles in a water suspension change the orientation of the magnetic moment and jump over unoccupied cubic lattice sites according to the Metropolis algorithm where the energy term in includes all the interaction potentials. Some fraction of magnetic nanoparticles penetrates the pores of the silica surface and sticks to the surface. The concentration of nanoparticles in the solution was chosen to be equal to to prevent agglomeration events in the solution. The diameter of pores was of the order of magnitude of the dimension of nanoparticle.

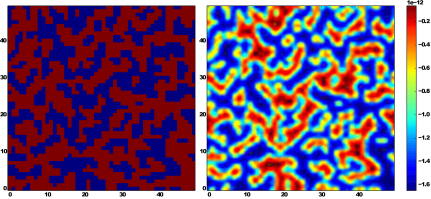
Fig. 2. On the left, a two-dimensional projection of the simulated silica surface is shown. Red and blue rectangles represent silica and pores respectively. On the right, the corresponding effective interaction potential (electrostatic and Van der Waals) is presented which is generated by the silica and felt by nanoparticle with radius nm in a solution with pH = 10 at distance nm from the silica surface

4. Results and discussion

Magnetic nanoparticles which are close to silica surface experience pH-dependent electrostatic potential which strongly depends on the distance to the surface. In Figure 2, it was shown both the two-dimensional projection of the silica surface (left panel) and the corresponding effective interaction potential (the sum of electrostatic interaction potential and Van der Waals interaction potential) of the simulated silica at at the distance nm (right panel) which is experienced by a single magnetic nanoparticle with diameter of 5 nm. The question arises to what extent the pH value affects the pore filling in the case when the size of the nanoparticle is comparable to the pore diameter. For such a value of pH as in Figure 2, magnetic nanoparticles experience strong electrostatic repulsion but still the Van der Waals attraction is a few orders higher than the electrostatic one. Our computer simulation suggests that the process of filling the silica pores by magnetic nanoparticles with dimension of the order of magnitude of the pore diameter does not depend on the pH value when the concentration of nanoparticles in the solution is low. Consequently, the density of nanoparticles in silica nano-pores weakly depends on the value of pH. It is evident in Figure 3, where the distribution of magnetic nanoparticles in the region close to the surface of the porous matrix has been shown for three values of pH (4, 7, and 10).

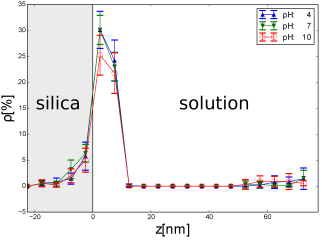
Fig. 3. Space dependence of the density of magnetic nanoparticles in the region close to the surface of the porous matrix which is contacting solution with a given value of pH is shown. All nanoparticles have a radius equal to nm. Three values of pH were chosen, pH = 4, 7, and 10

There is no significant difference between the fragments of the plots corresponding to the interior of silica. The effective potential experienced by magnetic nanoparticles approaching the silica surface strongly depends on their distance to the surface. In the case of large concentration of magnetic nanoparticles, the role of the value of pH increases. In paper [10], the preferential filling the silica pores by the alkaline solution with magnetic nanoparticles was observed. The results strongly depend on the value of PZC of the materials under consideration. In particular, in the case of magnetic iron oxide nanoparticles can take the value between 6.3 [5] and 7.9 [11]. In a magnetic suspension with the large concentration of magnetic nanoparticles, the dipolar magnetic interactions become important and they compete with the pH-dependent electrostatic repulsion between the nanoparticles.

5. Conclusions

A computer simulation of the process of filling the nanopores of the silica glass by water magnetic suspension at given value of pH was under discussion. It was concluded that pH value is significant for the surface adsorption of the nanoparticles but filling the pores by them weakly depends on the value of pH in the case of low concentration of magnetic nanoparticles.

Acknowledgements

We thank Bartłomiej Zapotoczny for his discussion and comments on the work.

References

[1] Lodhia J., Mandarano G., Ferris N.J., Eu P., Cowell S.F., Development and use of iron oxide nanoparticles (Part 1): Synthesis of iron oxide nanoparticles for MRI, Biomed. Imaging and Intervention Journal 2010, 6(2), e12.

[2] Huang S., Li C., Cheng Z., Fan Y., Yang P., Zhang C., Yang K., Lin J., Magnetic Fe₃O₄ mesoporous silica composites for drug delivery and bioadsorption, J. Colloid. Interf. Sci. 2012, 376, 312-321.

[3] Lu A.H., Salabas E.L., Schuth F., Magnetic nanoparticles: Synthesis, protection, functionalization, and application, Angew. Chem. Int. Ed. 2007, 46, 1222-1244.

[4] Zapotoczny B., Dudek M.R., Koziol J.J., Mleczko J., Nanobuffering property of Fe₃O₄ magnetic nanoparticles in aqueous solution, Physica A 2013, 392, 1493-1499.

[5] Borucka-Lipska J., Kiernozycki W., Guskos N., Dudek M.R., Ho D.Q., Wolak W., Marc M., Koziol J.J., Kalaga J.K., Investigation on magnetite concentrate with respect to its use in concrete, submitted.

[6] Gelb L.D., Gubbins K.E., Characterization of porous glasses: Simulation models, adsorption isotherms, and the Brunauer-Emmett-Teller analysis method, Langmuir 1998, 14(8), 2097-2111.

[7] Gelb L.D., Gubbins K.E., Pore size distributions in porous glasses: a computer simulation study, Langmuir 1999, 15(2), 305-308.

[8] Dudek M.R., Gouyet J.F., Kolb M., Q+ 1 state Potts model of late stage sintering, Surface Science 1998, 401(2), 220-226.

[9] Keren R., Sparks D.L., Effect of pH and ionic strength on boron adsorption by pyrophyllite, Soil Science Society of America Journal 1994, 58(4), 1095-1100.

[10] Zapotoczny B., Dudek M.R., Guskos N., Kozio J.J., Padlyak B.V., Kosmider M., Rysiakiewicz- -Pasek E., FMR study of the porous silicate glasses with Fe₃O₄ magnetic nanoparticles fillers, Journal of Nanomaterials 2012, 8.

[11] Tombacz E., Majzik A., Horvat Z.S., Illes E., Magnetite in aqueous medium: coating its surface and surface coated with it, Romanian Reports in Physics 2006, 58(3), 281-286.