On the convergence of multicomplex M-J sets to the Steinmetz hypersolids

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Katunin_2016,
   doi = {10.17512/jamcm.2016.3.07},
   url = {https://doi.org/10.17512/jamcm.2016.3.07},
   year = 2016,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {15},
   number = {3},
   pages = {67--74},
   author = {Andrzej Katunin},
   title = {On the convergence of multicomplex M-J sets to the Steinmetz hypersolids},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2016.3.07
UR  - https://doi.org/10.17512/jamcm.2016.3.07
TI  - On the convergence of multicomplex M-J sets to the Steinmetz hypersolids
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Katunin, Andrzej
PY  - 2016
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 67
EP  - 74
IS  - 3
VL  - 15
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Katunin, A. (2016). On the convergence of multicomplex M-J sets to the Steinmetz hypersolids. Journal of Applied Mathematics and Computational Mechanics, 15(3), 67-74. doi:10.17512/jamcm.2016.3.07

Katunin, A., 2016. On the convergence of multicomplex M-J sets to the Steinmetz hypersolids. Journal of Applied Mathematics and Computational Mechanics, 15(3), pp.67-74. Available at: https://doi.org/10.17512/jamcm.2016.3.07

[1]A. Katunin, "On the convergence of multicomplex M-J sets to the Steinmetz hypersolids," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 3, pp. 67-74, 2016.

Katunin, Andrzej. "On the convergence of multicomplex M-J sets to the Steinmetz hypersolids." Journal of Applied Mathematics and Computational Mechanics 15.3 (2016): 67-74. CrossRef. Web.

1. Katunin A. On the convergence of multicomplex M-J sets to the Steinmetz hypersolids. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(3):67-74. Available from: https://doi.org/10.17512/jamcm.2016.3.07

Katunin, Andrzej. "On the convergence of multicomplex M-J sets to the Steinmetz hypersolids." Journal of Applied Mathematics and Computational Mechanics 15, no. 3 (2016): 67-74. doi:10.17512/jamcm.2016.3.07

ON THE CONVERGENCE OF MULTICOMPLEX M-J SETS TO THE STEINMETZ HYPERSOLIDS

Andrzej Katunin

Institute of Fundamentals of Machinery Design, Silesian University of Technology
Gliwice, Poland
andrzej.katunin@polsl.pl

Abstract. In this paper, the analysis of generalized multicomplex Mandelbrot-Julia (henceforth abbrev. M-J) sets is performed in terms of their shape when a degree of an iterated polynomial tends to infinity. Since the multicomplex algebras result from a tensor product of complex algebras, the dynamics of multicomplex systems described by iterated polynomials is different with respect to their complex and hypercomplex analogues. When the degree of an iterated polynomial tends to infinity the M-J sets tend to the higher dimensional generalization of the Steinmetz solid, depending on the dimension of a vector space, where a given generalization of M-J sets is constructed. The paper describes a case of bicomplex M-J sets with appropriate visualizations as well as a tricomplex one, and the most general case - the muticomplex M-J sets, and their corresponding geometrical convergents.

Keywords: generalized M-J sets, multicomplex M-J sets, convergence, Steinmetz hypersolid

1. Introduction

The Mandelbrot set and corresponding Julia sets were intensively studied during the 80s of the XX century and many fascinating properties of these sets were observed to date. Considering that M-J sets are defined on a complex plane C in the form of a quadratic polynomial:

(1)

nothing stands in a way of generalization of these sets both in terms of degree of the polynomial as well as in terms of a vector space in which it is constructed. The first generalization of complex M-J sets to quaternionic H ones was defined by Holbrook [1], and then further developed and analysed by several authors [2-6]. Then, Wang and Sun [7] proposed a generalization of quaternionic M-J sets in terms of a degree of an iterated polynomial p:

(2)

However, these studies show that the dynamics of quaternionic maps is trivial with respect to their complex analogues. The same can be observed for the further generalization - the M-J sets in octonions O, introduced and studied by Griffin and Joshi in the early 90s of the XX century [8-10].

An alternative to the above-mentioned generalization was proposed by Rochon and his team. In 2000, Rochon introduced a generalization of M-J sets to a bicomplex vector space [11], further several studies on properties of this type of M-J sets [12-14] as well as their generalization to tricomplex [15] and multicomplex [16] analogues were proposed. The generalized version of bicomplex M-J sets with respect to a degree of an iterated polynomial was also studied by Zireh [17], and Wang and Song [18]. The performed studies of the above-mentioned teams show, in general, the different dynamics with respect to hypercomplex M-J sets which reflect, in particular, in varying character of changing a shape of these sets for varying values of a constant c in an iterated polynomial of type (2).

In the following study, the convergents of the multicomplex M-J sets, i.e. the sets for , are analysed. The study starts with the simplest case - the bicom- plex M-J sets, through the tricomplex ones, and ends with the most general case n-complex or multicomplex M-J sets. In each of the considered cases it was shown that the shapes of the convergents of M-J sets in multicomplex vector spaces tend to higher-dimensional generalizations of a Steinmetz solid.

2. Preliminaries to multicomplex algebras

Let us begin with the preliminaries of multicomplex vector spaces from the sim- plest case - a 4-algebra of bicomplex numbers . For simplicity, the following notation is introduced: C₂, where the lower index denotes a number of tensor product operations on complex algebras (thus C₂ denotes an algebra of bicomplex numbers, C₃ denotes an algebra of tricomplex numbers, etc.). The bicomplex numbers can be expressed in the symbolic representation as follows:

,

(3)

where are the associators, , and are the imaginary units with the following interrelations: , , . Since C₂ is commutative and considering the existence of idempotents for C₂ (which follows from the definition of bicomplex numbers):

,

(4)

where (or just C since C ≡ C₁), and are idempotents which means that during multiplication and do not change the initial result: , , , . C₂ is closed under addition and multiplication operations (which are necessary to perform an iteration of a polynomial of type (2)), and these operations can be performed element-wise. Considering that , , , , the addition and multiplication is defined as follows:

,

(5)

.

(6)

The next generalization of C₂ is an 8-algebra of tricomplex numbers C₃ with the following symbolic representation [15]:

,

(7)

with the following interrelations between imaginary units: , , , , . Similarly to C₂, the tri-complex numbers can be presented as a pair of bicomplex elements:

, ,

(8)

where and are idempotents, or in a form of a quadruple of complex elements:

, ,

(9)

, , , , the addition and multiplication of two tricomplex numbers and can be performed element-wise:

,

(10)

.

(11)

The above expressions can be generalized to a hypercomplex number space C_n, which is n-tensor product 2ⁿ-algebra with a following symbolic representation [19]:

,

(12)

where , or alternatively:

,

(13)

where , . Thus, every multicomplex number in C_n contains 2ⁿ elements with the associators defined in R, or equivalently 2^n–m elements defined in C_m for .

The multicomplex algebra is commutative and idempotent representation of multicomplex number has the form [16]:

,

(14)

where and are idempotents. Extending (5)-(6) and (10)-(11) to the case of C_n the addition and multiplication operations of two multi-complex numbers and can be performed element-wise as:

,

(15)

.

(16)

3. Multicomplex M-J sets

Having defined multicomplex algebras and basic operations on multicomplex numbers, one can define M-J sets as follows:

for ,

(17)

and correspondingly:

for .

(18)

The authors of [16] proved that M sets and filled J sets defined in C_n are connected and the escaping-time radius (known also as a bailout values) equals 2. Moreover, the connectedness of J sets defined in C_n are of three types: connected, when , totally disconnected (i.e. homeomorphic to the Cantor dust) when and , where is a strong basin of attraction at infinity (see details in [16]), and disconnected, but not totally in all other cases. More details on connectedness and other properties of M-J sets defined in C_n can be found in [16].

4. Convergence analysis

When changing a degree p of an iterated polynomial of type (2) significant changes in a shape of the resulting M-J sets can be observed for the small values of p. However, when , a shape of these sets tends to a specific geometrical shape. An example of such behavior for is presented in Figure 1.

(a) ; (b) ; (c) ;

(d) ; (d) ; (f) ;

Fig. 1. 3D projections of bicomplex J sets for c = (–0.5,0.5,0,0) and various values of p

Theorem 1. The generalized bicomplex M-J sets of type (2) tend to a 4-dimen-sional Steinmetz solid when .

Before proceeding with the proof of the Theorem 1, it is necessary to define the generalized n-dimensional Steinmetz solid or the Steinmetz hypersolid.

Definition 1. We say that the Steinmetz hypersolid is an n-dimensional solid resulting from an intersection of Q n-cylinders (Q ≥ 2) of equal radii r denoted as , where , is a q-th coordinate axis and is a unitary basis in Rⁿ unique for each q, and being their common:

.

(19)

Proof. Suppose c = 0 in (2) defined in bicomplex numbers which is equivalent to the case when . Then (2) takes a form:

, , .

(20)

Recalling representation of a product of two bicomplex numbers by pairs of complex numbers (6), one can present (20) in the following form [20]:

,

(21)

where , x_1,…,4 are the coordinates in C₂. Following this, we can rewrite (20) in the form:

,

(22)

and considering that C₂ results from a tensor product , the boundary of sets of prisoner points, i.e. the M and “filled” J sets are given by a common of intersection of two 3-cylinders:

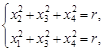(23)

where r = 1. In the limit case (when ) the resulting set does not have fractal properties. The system (23) describes .

Corollary 1. One can extend Theorem 1 as follows: The generalized tricomplex M-J sets of type (2) tend to 8-dimensional Steinmetz solid when .

Proof. Considering Definition 1 and a recursive equation (20) defined in C₃, one can express such an equation in terms of quadruple of complex numbers as follows:

.

(24)

By analogy to the proof of Theorem 1, the tricomplex M-J sets tend to given by:

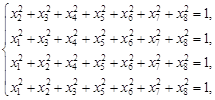(25)

when .

Corollary 2. One can also extend Theorem 1 to the most general form: The generalized multicomplex M-J sets of type (2) tend to an n-dimensional Steinmetz solid when .

Proof. Considering Definition 1 and a recursive equation (20) defined in C_n one can express such equation in terms of n/2-tuple of complex numbers. By analogy to the proofs of Theorem 1 and Corollary 1, the multicomplex M-J sets tend to given by:

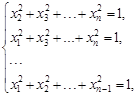(26)

when .

5. Conclusions

In the presented study, the convergents of multicomplex M-J sets were investigated. Starting from the simplest case - the bicomplex algebra, it was shown that in contrast to hypercomplex generalizations of M-J sets [21], the multicomplex ones tend to higher dimensional Steinmetz solids (with ) which, in a general case, results from the intersection of n/2 n-cylinders in C_n .

References

[1] Holbrook J.A.R., Quaternionic Fatou-Julia sets, Ann. Sci. Math. Québec 1987, 11, 79-94.

[2] Norton A.V., Julia sets in the quaternions, Comput. Graph. 1989, 13(2), 267-278.

[3] Gomatam J., Doyle J., Steves B., McFarlane I., Generalization of the Mandelbrot set: quaternionic quadratic maps, Chaos Soliton. Fract. 1995, 5(6), 971-986.

[4] Bedding S., Briggs K., Iteration of quaternion maps, Int. J. Bifurcat. Chaos 1995, 5(3), 877-881.

[5] Petek P., Circles and periodic points in quaternionic Julia sets, Open Syst. Inf. Dyn. 1997, 4(4), 487-492.

[6] Lakner M., Petek P., The one-equator property, Experiment. Math. 1997, 6(2), 109-115.

[7] Wang X.Y., Sun Y.Y., The general quaternionic M-J sets on the mapping z ← z^α + c, Comput. Math. Appl. 2007, 53(11), 1718-1732.

[8] Griffin C.J., Joshi G.C., Octonionic Julia sets, Chaos Soliton. Fract. 1992, 2(1), 11-24.

[9] Griffin C.J., Joshi G.C., Transition points in octonionic Julia sets, Chaos Soliton. Fract. 1993, 3(1), 67-88.

[10] Griffin C.J., Joshi G.C., Associators in generalized octonionic maps, Chaos Soliton. Fract. 1993, 3(3), 307-319.

[11] Rochon D., Generalized Mandelbrot set for bicomplex numbers, Fractals 2000, 8(4), 355-368.

[12] Rochon D., On a generalized Fatou-Julia theorem, Fractals 2003, 11(3), 213-219.

[13] Martineau É., Rochon D., On a bicomplex distance estimation for the Tetrabrot, Int. J. Bifurcat. Chaos 2005, 15(9), 3039-3050.

[14] Matteau C., Rochon D., The inverse iteration method for Julia sets in the 3-dimensional space, Chaos Soliton. Fract. 2015, 75, 272-280.

[15] Parisé P.O., Rochon D., A study on dynamics of the tricomplex polynomial η^p + c, Nonlin. Dyn. 2015, 82(1), 157-171.

[16] Garant-Pelletier V., Rochon D., On a generalized Fatou-Julia theorem in multicomplex spaces, Fractals 2009, 17(3), 241-255.

[17] Zireh A., A generalized Mandelbrot set of polynomials of type E_d for bicomplex numbers, Georgian Math. J. 2008, 15(1), 189-194.

[18] Wang X.Y., Song W.J., The generalized M-J sets for bicomplex numbers, Nonlin. Dyn. 2013, 72(1), 17-26.

[19] Price G.B., An Introduction to Multicomplex Spaces and Functions, Marcel Dekker Inc., New York 1991.

[20] Rönn S., Bicomplex algebra and function theory, arXiv: math/0101200v1, 2001, 1-71.

[21] Katunin A., Fedio K., On a visualization of the convergence of the boundary of generalized Mandelbrot set to (n-1)-sphere, J. Appl. Math. Comput. Mech. 2015, 14(1), 63-69.