The non-Keller mapping with one zero at infinity

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Biernat_2016,
   doi = {10.17512/jamcm.2016.4.01},
   url = {https://doi.org/10.17512/jamcm.2016.4.01},
   year = 2016,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {15},
   number = {4},
   pages = {5--10},
   author = {Grzegorz Biernat and  Anita Ciekot},
   title = {The non-Keller mapping with one zero at infinity},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2016.4.01
UR  - https://doi.org/10.17512/jamcm.2016.4.01
TI  - The non-Keller mapping with one zero at infinity
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Biernat, Grzegorz
AU  - Ciekot, Anita
PY  - 2016
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 5
EP  - 10
IS  - 4
VL  - 15
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Biernat, G., & Ciekot, A. (2016). The non-Keller mapping with one zero at infinity. Journal of Applied Mathematics and Computational Mechanics, 15(4), 5-10. doi:10.17512/jamcm.2016.4.01

Biernat, G. & Ciekot, A., 2016. The non-Keller mapping with one zero at infinity. Journal of Applied Mathematics and Computational Mechanics, 15(4), pp.5-10. Available at: https://doi.org/10.17512/jamcm.2016.4.01

[1]G. Biernat and A. Ciekot, "The non-Keller mapping with one zero at infinity," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 4, pp. 5-10, 2016.

Biernat, Grzegorz, and Anita Ciekot. "The non-Keller mapping with one zero at infinity." Journal of Applied Mathematics and Computational Mechanics 15.4 (2016): 5-10. CrossRef. Web.

1. Biernat G, Ciekot A. The non-Keller mapping with one zero at infinity. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(4):5-10. Available from: https://doi.org/10.17512/jamcm.2016.4.01

Biernat, Grzegorz, and Anita Ciekot. "The non-Keller mapping with one zero at infinity." Journal of Applied Mathematics and Computational Mechanics 15, no. 4 (2016): 5-10. doi:10.17512/jamcm.2016.4.01

THE NON-KELLER MAPPING WITH ONE ZERO AT INFINITY

Grzegorz Biernat, Anita Ciekot

Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
anita.ciekot@im.pcz.pl, grzegorz.biernat@im.pcz.pl
Received: 24 September 2016; accepted: 15 November 2016

Abstract. In this paper the polynomial mapping of two complex variables having one zero at infinity is considered. Unlike with Keller mapping, if determinant of the Jacobian of this mapping is constant then it must be zero.

Keywords: Jacobian, zero at infinity, polynomial mappings, Keller mappings

1. Introduction

The main question of this paper concerns an attempt to analyze the problems connected with the special kind of polynomial mapping of two complex variables: non-Keller mapping. In [1, 2] the rare mappings with one zero at infinity was analyzed. It is shown that the Jacobian of non-Keller mapping being constant must vanish. It is a new mapping unlike with Keller maps that were studied over the last fifteen years [3-6].

In the generic case, the polynomial mappings with one zero at infinity are probably non-invertible. Namely, let

(1)

and

(2)

be coordinates of the polynomial mappings of two complex variables.

Now, let . It seems that in the generic case, if then .

2. The non-invertible mapping

Let

(3)

and

(4)

where . The forms have degree .

Let additionally

(5)

where .

Lemma. Let

(6)

Then

(7)

Proof. Let

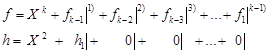(8)

where .

In the next steps we have

(9)

so

(10)

and

(11)

We assume further that

(12)

Substituting (11) into (12) we get

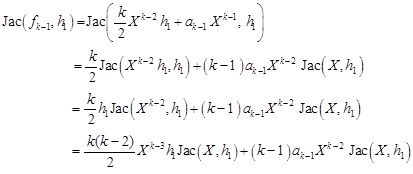(13)

Therefore from (12) we obtain

(14)

Hence, dividing by , we have

(15)

Subsequently

(16)

(17)

Substituting (16) into (17) we get

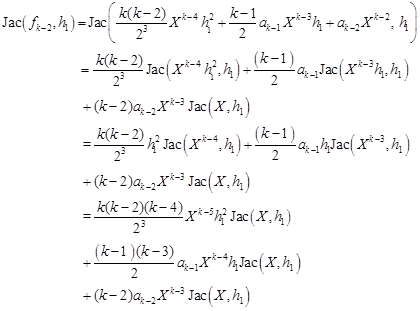(18)

Therefore the formula (17) gives

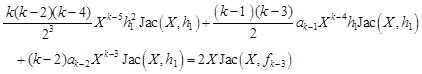(19)

Similarly, dividing by , we have

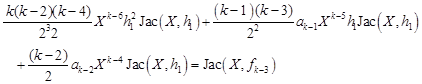(20)

Consequently

(21)

etc.

Case 1. Suppose

(22)

In the step we obtain

(23)

Therefore divides , so

(24)

and

(25)

Subsequently

(26)

Case 2. Suppose

(27)

Then

(28)

where .

In the step we obtain

(29)

Therefore divides , so

(30)

and

(31)

Subsequently

(32)

This completes the proof.

3. Conclusion

In this paper the particular case of the form h for was investigated. It is not hard to show that if then . Consequently, in a similar way, we can prove that if the determinant of non-Keller mapping is constant then in generic case, it must vanish.

It seems that in the case the second coordinates of considering mapping has the form .

References

[1] Pawlak E., Lara-Dziembek S., Biernat G., Woźniakowska M., An example of non-Keller mapping, Journal of Applied Mathematics and Computational Mechanics 2016, 15(1), 115-121.

[2] Pawlak E., Lara-Dziembek S., Biernat G., Woźniakowska M., A second example of non-Keller mapping, Journal of Applied Mathematics and Computational Mechanics 2016, 15(2), 65-70.

[3] Wright D., On the Jacobian conjecture, no. 3, Illinois J. Math. 1981, 25, 423-440.

[4] Van den Essen A., Polynomial automorphisms and the Jacobian conjecture, Progress in Matematics 190, Birkhäuser Verlag, Basel 2000.

[5] Van den Essen A., Hubbers E., Ploynomial maps with strongly nilpotent Jacobian matrix and he Jacobian conjecture, Linear Algebra and Its Applications 1996, 247, 121-132.

[6] Bass H., Connell E.H., Wright D., The Jacobian conjecture: reduction of degree and formal expansion of the inverse, American Mathematical Society, Bulletin, New Serie 1982, 7(2), 287-330.