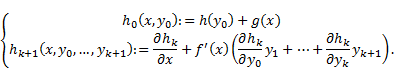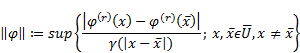Solutions of some functional equations in a class of generalized Hölder functions
Maria Lupa
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Lupa_2016,
doi = {10.17512/jamcm.2016.4.12},
url = {https://doi.org/10.17512/jamcm.2016.4.12},
year = 2016,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {15},
number = {4},
pages = {105--116},
author = {Maria Lupa},
title = {Solutions of some functional equations in a class of generalized Hölder functions},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2016.4.12 UR - https://doi.org/10.17512/jamcm.2016.4.12 TI - Solutions of some functional equations in a class of generalized Hölder functions T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Lupa, Maria PY - 2016 PB - The Publishing Office of Czestochowa University of Technology SP - 105 EP - 116 IS - 4 VL - 15 SN - 2299-9965 SN - 2353-0588 ER -
Lupa, M. (2016). Solutions of some functional equations in a class of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics, 15(4), 105-116. doi:10.17512/jamcm.2016.4.12
Lupa, M., 2016. Solutions of some functional equations in a class of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics, 15(4), pp.105-116. Available at: https://doi.org/10.17512/jamcm.2016.4.12
[1]M. Lupa, "Solutions of some functional equations in a class of generalized Hölder functions," Journal of Applied Mathematics and Computational Mechanics, vol. 15, no. 4, pp. 105-116, 2016.
Lupa, Maria. "Solutions of some functional equations in a class of generalized Hölder functions." Journal of Applied Mathematics and Computational Mechanics 15.4 (2016): 105-116. CrossRef. Web.
1. Lupa M. Solutions of some functional equations in a class of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2016;15(4):105-116. Available from: https://doi.org/10.17512/jamcm.2016.4.12
Lupa, Maria. "Solutions of some functional equations in a class of generalized Hölder functions." Journal of Applied Mathematics and Computational Mechanics 15, no. 4 (2016): 105-116. doi:10.17512/jamcm.2016.4.12
SOLUTIONS OF SOME FUNCTIONAL EQUATIONS IN A CLASS OF GENERALIZED HÖLDER FUNCTIONS
Maria Lupa
Institute of Mathematics, Częstochowa
University of Technology
Częstochowa, Poland
maria.lupa@im.pcz.pl
Received: 17 October
2016; accepted: 15 November 2016
Abstract. The
existence and uniqueness of solutions a nonlinear iterative equation
in the class of ![]() -times
differentiable functions with the
-times
differentiable functions with the ![]() -derivative satisfying
a generalized Hölder condition is considered.
-derivative satisfying
a generalized Hölder condition is considered.
Keywords: iterative functional equation, generalized Hölder condition
1. Introduction
In [1, 2]
the space ![]() (
(![]() ) of
) of ![]() times differentiable functions with the
times differentiable functions with the ![]() -the derivative satisfying generalized
-the derivative satisfying generalized ![]() -Hölder condition was introduced
and some of its properties proved. In the present paper we examine the
existence and uniqueness of solutions of a nonlinear iterative functional
equation in this class of functions. We apply some ideas from Kuczma [3],
Matkowski [4, 5] (see also Kuczma, Choczewski, Ger [6]), where differentiable
solutions, Lipschitzian
solutions, bounded variation solutions of different type of itrerative
functional equations were investigated.
-Hölder condition was introduced
and some of its properties proved. In the present paper we examine the
existence and uniqueness of solutions of a nonlinear iterative functional
equation in this class of functions. We apply some ideas from Kuczma [3],
Matkowski [4, 5] (see also Kuczma, Choczewski, Ger [6]), where differentiable
solutions, Lipschitzian
solutions, bounded variation solutions of different type of itrerative
functional equations were investigated.
2. Preliminaries
Consider non-linear functional equation
| (1) |
where ![]() are given and
are given and ![]() is a unknown function.
is a unknown function.
We accept the following notation: ![]() ,
, ![]() - is the Banach space
of the r-time differentiable functions defined on the interval
- is the Banach space
of the r-time differentiable functions defined on the interval ![]() with values in
with values in ![]() , such that, for some
, such that, for some ![]() ; its r-th derivative satisfies the
following
; its r-th derivative satisfies the
following ![]() -Hölder condition
-Hölder condition
where a fixed function ![]() satisfies
the following condition (see [1, 2]):
satisfies
the following condition (see [1, 2]):
| (Γ)
|
We assume that
(i) ![]()
(ii) ![]()
(iii) ![]() fulfils the Lipschitz
condition in
fulfils the Lipschitz
condition in ![]()
(iv) there exists ![]() such that
such that![]() , where
, where ![]() is
the n-th iteration function
is
the n-th iteration function ![]()
(v) is analityc function at ![]() , where
, where ![]() is the solution of
equation
is the solution of
equation
![]()
We
define functions ![]() by the formula
by the formula
|
|
Lemma 1. [4]
By assumptions (i)-(iii), ![]() defined by (2) are of
the form:
defined by (2) are of
the form:
1. for
![]()
| (3) |
2. for
![]()
| (4) |
where
| (5) |
and ![]() are of the class
are of the class ![]() in I, for all
numbers
in I, for all
numbers ![]() such that
such that ![]()
Remark 1.
If (i)-(iii) are fulfilled, then ![]() given by
given by
fulfill ![]() -Hölder condition for
-Hölder condition for
![]() and Lipschitz
condition with respect to
and Lipschitz
condition with respect to ![]() in
in ![]() [
[![]() . It means, that there
are positive constants
. It means, that there
are positive constants ![]() and
and
such that for ![]() ,
,![]() we have
we have
Define the functions ![]() by the following
formulas:
by the following
formulas:
| (6) |
Remark 2.
The functions ![]() defined by (6) fulfill
defined by (6) fulfill ![]() -Hölder condition with respect to variable x in
I and Lipschitz condition with respect to the variable
-Hölder condition with respect to variable x in
I and Lipschitz condition with respect to the variable ![]() in each
set
in each
set ![]()
Remark 3.
If ![]() satisfy the assumptions
(i)-(iii) and
satisfy the assumptions
(i)-(iii) and ![]() is a solution of
equation (1) then the derivatives
is a solution of
equation (1) then the derivatives ![]() satisfy the system of
equations
satisfy the system of
equations
If assumptions (i)-(iv) are fulfilled and ![]() is a solution of
equation (1) in
is a solution of
equation (1) in ![]() , then the
numbers
, then the
numbers
| (7) |
satisfy the system of equations
| (8) |
where ![]() are defined by (2).
are defined by (2).
Remark 4.
Let ![]() be a solution of the
equation (1). Present
be a solution of the
equation (1). Present ![]() in the following form
in the following form
| (9) |
where ![]() and
and ![]()
Define the functions
and for ![]() ,
, ![]()
It follows from above definitions and equation (9) that 𝜓 satisfies the following equation
It is easy to prove, that if assumptions
(i)-(iv) are fulfilled and ![]() are the solution of
equations (8), then the function
are the solution of
equations (8), then the function ![]() satisfies the equation
(1) in
satisfies the equation
(1) in ![]() and the condition (7)
if and only if the function
and the condition (7)
if and only if the function ![]() given by (9) belongs
to
given by (9) belongs
to ![]() and satisfies
and satisfies
Thus, we assume that ![]() and consider the equation (1) whose solution satisfies the
condition
and consider the equation (1) whose solution satisfies the
condition
Then system of equations (8) takes the following form
3. Main result
Theorem 1.
If assumptions (i)-(iii) are fulfilled, ![]() is a monotone function in the interval I, the conditions (iv) and
(v) are fulfilled for
is a monotone function in the interval I, the conditions (iv) and
(v) are fulfilled for ![]()
![]() and
and
| (10) |
| (11) |
then equation (1) has exactly one solution ![]() satisfying the
condition
satisfying the
condition
| (12) |
Moreover, there exists a neighbourhood ![]() of the point
of the point ![]() and the number
and the number ![]() such that for a
function
such that for a
function ![]() , satisfying the
condition (12) and the inequality
, satisfying the
condition (12) and the inequality ![]() , a sequence of
functions
, a sequence of
functions
converges to a solution of (1) according to the
norm in the space ![]()
Proof.
From (v) we have ![]() in some neighbourhood of the point
in some neighbourhood of the point ![]() .
Denote by
.
Denote by ![]() the radius of
convergence of this series. From (11) and from
the continuity of functions
the radius of
convergence of this series. From (11) and from
the continuity of functions ![]() and
and ![]() , from definition of the function
, from definition of the function ![]() there
exists a neighbourhood
there
exists a neighbourhood ![]() of the point
of the point ![]() and
and ![]() such that
such that
| (13) |
From Remark 1, definition of ![]() and from (13) there are positive constants
and from (13) there are positive constants ![]() and
and ![]() , that in
, that in ![]() we have
we have
| (14) |
From Remark 2, definition of ![]() there are in
there are in ![]() constants
constants ![]() ,
, ![]() such that
such that
| (15) |
We accept the following notation:
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
By ![]() we denote the sum of
we denote the sum of ![]() for all
for all ![]() such that
such that ![]()
In view of Lemma 1, we have
and, from (13), we get
| (21) |
Let us take ![]() and
and
Put
|
|
|
Then let’s take ![]() such that
such that ![]() and
and
| (23) |
Choose ![]() . Of course
. Of course ![]() . We will select a
neighborhood of zero
. We will select a
neighborhood of zero ![]() such that
such that ![]() and
and ![]() .
.
Consider the Banach space ![]() with the norm:
with the norm:
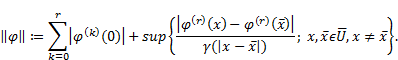 |
Let us define the set
Note that ![]() is a closed subset of
Banach space
is a closed subset of
Banach space ![]() and for
and for ![]() the norm is expressed
by the formula
the norm is expressed
by the formula
|
|
Thus, the set ![]() with the metric
ϱ(
with the metric
ϱ(![]() is a complete metric
space.
is a complete metric
space.
By the mean value theorem and by definition of
the number of c we have for ![]()
| (25) |
and so ![]()
For ![]() define the
transformation
define the
transformation ![]() by the
formula
by the
formula
We will show that ![]()
Based on Remarks 1 and 3 the function ![]() belongs to
belongs to ![]() from (iv) and (10),
(12) appears that
from (iv) and (10),
(12) appears that ![]() . Then using the
formulas (12), (13), (22), (25) and the assumption (i) we obtain
. Then using the
formulas (12), (13), (22), (25) and the assumption (i) we obtain
Which means from (24) that ![]() . Thus
. Thus ![]() .
.
Now we prove that T is a contraction map. Let us
put ![]() ,
, ![]() .
Basing on formulas (4)-(5) of Lemma 1 and from (24) we have
.
Basing on formulas (4)-(5) of Lemma 1 and from (24) we have
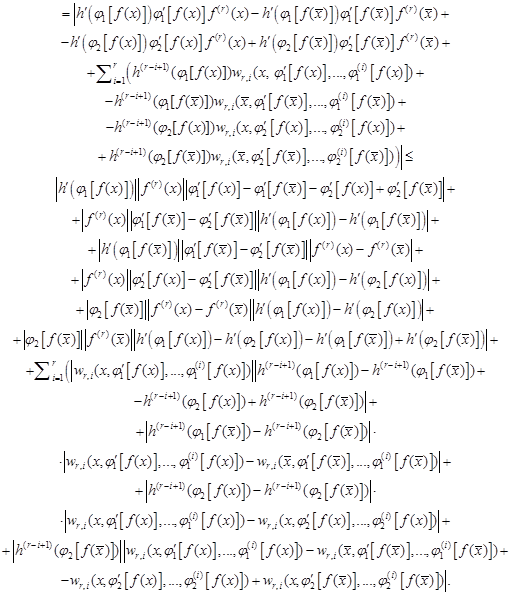 |
Note, that if ![]() , then in view of the
mean value theorem, from
the definition of the number
, then in view of the
mean value theorem, from
the definition of the number ![]() and from (i) we have
the following inequalities
and from (i) we have
the following inequalities
| (26) |
| (27) |
| (28) |
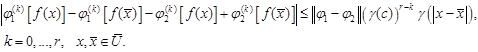 | (29) |
By induction on ![]() we
also obtain:
we
also obtain:
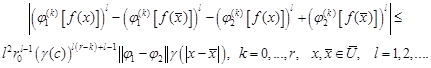 | (30) |
From (v) and by selection of ![]() we have uniform and absolute
convergence of
the series
we have uniform and absolute
convergence of
the series
Let's consider the expression:
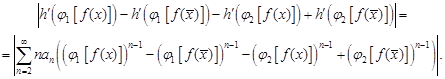 |
From (30) we obtain
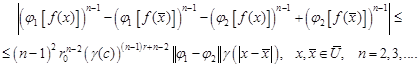 |
Note that a series
converges, because the numbers ![]() have been selected in such a way that
have been selected in such a way that
Therefore
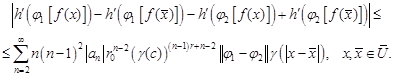 | (31) |
Similarly for ![]() we
get
we
get
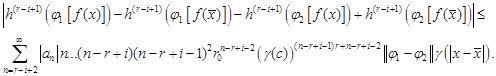 | (32) |
By induction and from (26)-(29) we have
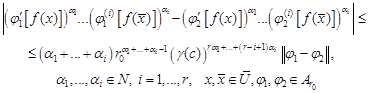 | (33) |
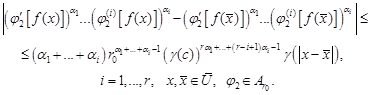 | (34) |
Now from (33) and (34) we get
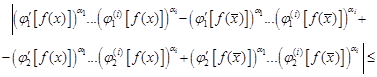
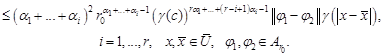 | (35) |
From (6), by the mean value theorem and from (33) and (34) we get
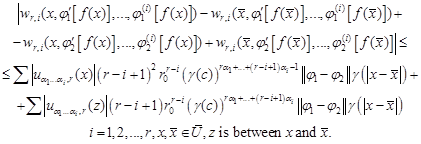 | (36) |
Now, from (15)-(22), (27)-(32) and (36) we get
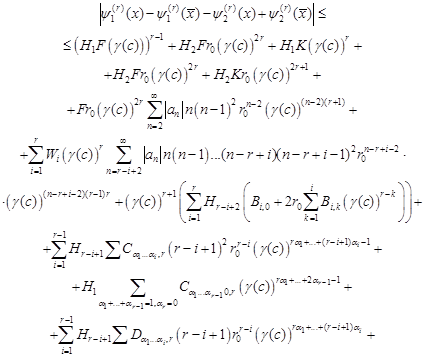
|
Putting ![]() and making use
of definition (24) of the norm in
and making use
of definition (24) of the norm in ![]() we have
we have
which means that ![]() ,
where
,
where ![]() in view on (23).
in view on (23).
By the
Banach fixed point theorem, there is exactly one solution ![]() of (1) satisfying the condition (12). This solution is given
as the limit of series of successive approximations.
of (1) satisfying the condition (12). This solution is given
as the limit of series of successive approximations.
where ![]() . This sequence converges in the sense of the norm of
. This sequence converges in the sense of the norm of ![]() .
By Lemma 4 in [7], there exists the unique extension
.
By Lemma 4 in [7], there exists the unique extension ![]() of
of ![]() to
the whole interval
to
the whole interval ![]() such that
such that ![]() for
for ![]() and
and ![]() satisfies the equation (1) in
satisfies the equation (1) in ![]() . This completes the proof.
. This completes the proof.
Conclusions
In this paper, applying the Banach
contraction principle, a theorem on the existence and uniqueness of ![]() -solutions of nonlinear iterative
functional equation (1) has been proved. The suitable unique solution is
determined as a limit of sequence of successive approximations.
-solutions of nonlinear iterative
functional equation (1) has been proved. The suitable unique solution is
determined as a limit of sequence of successive approximations.
References
[1] Lupa M., A special case of generalized Hölder functions, Journal of Applied Mathematics and Computational Mechanics 2014, 13(4), 81-89.
[2] Lupa M., On a certain property of generalized Hölder functions, Journal of Applied Mathematics and Computational Mechanics 2015, 14(4), 127-132.
[3] Kuczma M., Functional Equations in a Single Variable, PWN, Warszawa 1968.
[4] Matkowski J., On the uniqueness of differentiable solutions of a functional equation, Bulletin de l’Academie des Sciences, Serie des sciences math., astr. et phys. 1970, XVIII, 5, 253-255.
[5] Matkowski J., On the existence of differentiable solutions of a functional equation, Bulletin de l’Academie des Sciences, Serie des sciences math., astr. et phys. 1971, XIX, 1, 19-21.
[6] Kuczma M., Choczewski B., Ger R., Iterative Functional Equations, Cambridge University Press, Cambridge-New York-Port Chester-Melbourne-Sydney 1990.
[7] Lupa M., On solutions of a functional equation in a special class of functions, Demonstratio Mathematica 1993, XXVI, 1, 137-147.