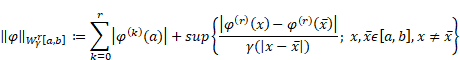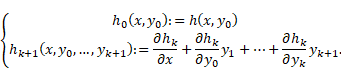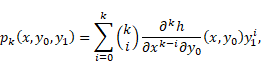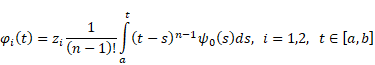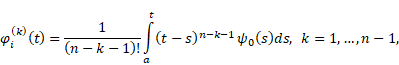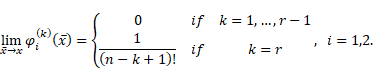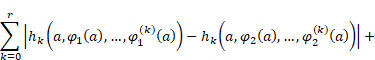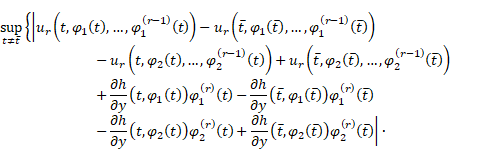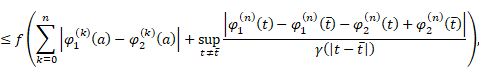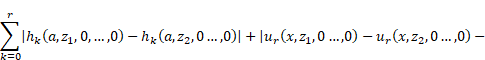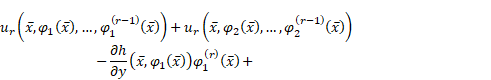Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions
Maria Lupa
,Małgorzata Wróbel
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Lupa_2017,
doi = {10.17512/jamcm.2017.4.04},
url = {https://doi.org/10.17512/jamcm.2017.4.04},
year = 2017,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {16},
number = {4},
pages = {37--45},
author = {Maria Lupa and Małgorzata Wróbel},
title = {Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2017.4.04 UR - https://doi.org/10.17512/jamcm.2017.4.04 TI - Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Lupa, Maria AU - Wróbel, Małgorzata PY - 2017 PB - The Publishing Office of Czestochowa University of Technology SP - 37 EP - 45 IS - 4 VL - 16 SN - 2299-9965 SN - 2353-0588 ER -
Lupa, M., & Wróbel, M. (2017). Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics, 16(4), 37-45. doi:10.17512/jamcm.2017.4.04
Lupa, M. & Wróbel, M., 2017. Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics, 16(4), pp.37-45. Available at: https://doi.org/10.17512/jamcm.2017.4.04
[1]M. Lupa and M. Wróbel, "Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions," Journal of Applied Mathematics and Computational Mechanics, vol. 16, no. 4, pp. 37-45, 2017.
Lupa, Maria, and Małgorzata Wróbel. "Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions." Journal of Applied Mathematics and Computational Mechanics 16.4 (2017): 37-45. CrossRef. Web.
1. Lupa M, Wróbel M. Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2017;16(4):37-45. Available from: https://doi.org/10.17512/jamcm.2017.4.04
Lupa, Maria, and Małgorzata Wróbel. "Uniformly bounded Nemytskij operators acting between the Banach spaces of generalized Hölder functions." Journal of Applied Mathematics and Computational Mechanics 16, no. 4 (2017): 37-45. doi:10.17512/jamcm.2017.4.04
UNIFORMLY BOUNDED NEMYTSKIJ OPERATORS ACTING BETWEEN THE BANACH SPACES OF GENERALIZED HÖLDER FUNCTIONS
Maria Lupa, Małgorzata Wróbel
Institute of Mathematics, Czestochowa
University of Technology
Czestochowa, Poland
maria.lupa@im.pcz.pl, malgorzata.wrobel@im.pcz.pl
Received: 23 October 2017;
Accepted: 13 November 2017
Abstract. We
investigate the Nemytskij (composition, superposition) operators acting
between Banach spaces of ![]() -times differentiable
functions defined on the closed intervals of the real line with the
-times differentiable
functions defined on the closed intervals of the real line with the ![]() -derivatives satisfying a generalized Hölder condition. The main
result says that if such a Nemytskij operator is uniformly bounded (in a
special case
uniformly continuous) then its generator is an affine function with respect to
the second variable, i.e., the Matkowski representation holds. This extends an
earlier result where
an operator is assumed to be Lipschitzian.
-derivatives satisfying a generalized Hölder condition. The main
result says that if such a Nemytskij operator is uniformly bounded (in a
special case
uniformly continuous) then its generator is an affine function with respect to
the second variable, i.e., the Matkowski representation holds. This extends an
earlier result where
an operator is assumed to be Lipschitzian.
MSC 2010: 47H30, 26A11
Keywords: Nemytskij (composition, superposition) operator, generalized Hölder condition, uniformly bounded mapping, uniformly continuous mapping
1. Introduction
The Nemytskij operators occur frequently in the theory of integral equations, differential equations, variational calculus or in optimization theory. There is vast literature devoted to applications of the results connected with the theory of the composition operators (see, for instance [1], where such operators occur in the problems of option pricing within the Black-Scholes model for time-dependent volatility).
Let![]() be an interval of the
real line
be an interval of the
real line![]() (
(![]() ) and let
) and let ![]() denote the set of all functions
denote the set of all functions ![]() For a given function
For a given function ![]() , the mapping
, the mapping ![]() defined by
defined by
is called a composition (Nemytskij or
superposition) operator of a generator![]() .
.
In 1982 J. Matkowski [2] proved that if H
maps a Banach space ![]() of Lipschitzian
functions
of Lipschitzian
functions ![]() with the classical
with the classical ![]() -norm into itself and
is globally Lipschitzian, i.e., if for some constant
-norm into itself and
is globally Lipschitzian, i.e., if for some constant ![]() ,
,
then
| (1) |
for some functions ![]() i.e., h is an
affine function with respect to the second variable. Analogous results for
representations of the generators of globally Lipschitzian operators have been
proved for some other function spaces [3-7]. Later, it was observed that these
results remain true if the Lipschitz norm-continuity of H is replaced by its
uniform continuity [8, 9].
i.e., h is an
affine function with respect to the second variable. Analogous results for
representations of the generators of globally Lipschitzian operators have been
proved for some other function spaces [3-7]. Later, it was observed that these
results remain true if the Lipschitz norm-continuity of H is replaced by its
uniform continuity [8, 9].
In 2011, J. Matkowski [10] proved, under very general assumptions, that for the function spaces including the Hölder spaces as a special case, the uniform continuity of the operator H can be replaced by a much weaker condition of the uniform boundedness (which is weaker than norm-boundedness), see also [11, 12].
The purpose of this paper is to show that if ![]() maps the space
maps the space ![]() of
of
![]() -times differentiable
functions with the
-times differentiable
functions with the ![]() -derivative
satisfying a generalized Hölder condition into
-derivative
satisfying a generalized Hölder condition into ![]() , where
, where ![]() and
and ![]() is uniformly
bounded, then the Matkowski representation holds, i.e., the generator
is uniformly
bounded, then the Matkowski representation holds, i.e., the generator ![]() of
of ![]() must be of the form (1)
for some
must be of the form (1)
for some ![]() . This extends the main
result of [5, 6] where
. This extends the main
result of [5, 6] where ![]() is
assumed to be Lipschitzian.
is
assumed to be Lipschitzian.
2. Preliminaries
Given a closed interval ![]() (
(![]()
![]() put
put ![]() . Let
. Let ![]()
![]() following condition:
following condition:
(Γ) ![]() is increasing and concave, γ(0) = 0,
is increasing and concave, γ(0) = 0, ![]() ,
,
![]()
Given ![]() , denote by
, denote by ![]() the set of all r-times
differentiable functions
the set of all r-times
differentiable functions ![]() such that their r-th
derivatives satisfy the following condition (so called the generalized
Hölder condition or the
such that their r-th
derivatives satisfy the following condition (so called the generalized
Hölder condition or the ![]() -Hölder condition):
there exists
a constant
-Hölder condition):
there exists
a constant ![]() such that
such that
| (2) |
where ![]()
![]() satisfy condition (Γ).
satisfy condition (Γ).
It is known that the space ![]() endowed with the norm
endowed with the norm
|
|
is a Banach space [3, 4].
Let ![]() ,
, ![]() stand for the class of
all r-times differentiable functions
stand for the class of
all r-times differentiable functions ![]() , whose r-th
derivatives satisfy the Lipschitz condition on
, whose r-th
derivatives satisfy the Lipschitz condition on ![]() .
.
Remark 2.1. Observe,
that if ![]() with the constant
with the constant ![]() , then
, then ![]() fulfils (2) with the constant
fulfils (2) with the constant ![]() .
.
Indeed, by ![]() , we get the
monotonicity of the function
, we get the
monotonicity of the function
|
|
and, consequently, we have
for all ![]()
Remark 2.2 ([6], Remark 1). If ![]() and
and ![]() is finite,
is finite, ![]() denotes the right
derivative of γ at
denotes the right
derivative of γ at ![]() then
then ![]()
![]()
Remark 2.3. Let us notice that the function defined by ![]() , where
, where ![]() ,
, ![]() , fulfils the
assumption
, fulfils the
assumption ![]() and
and ![]() .
.
Definition 2.1. Let ![]() and a function
and a function ![]() be fixed. The mapping
be fixed. The mapping ![]() given by
given by
is said to be a composition (Nemytskij or superposition) operator. The function h is referred to as the generator of the operator H.
Assume now, that the function h fulfils the following condition:
(i) ![]() is
is ![]() -times differentiable in
-times differentiable in ![]() ,
, ![]() , and all its r-th
order partial derivatives fulfill the generalized
Hölder conditions with respect to
the first variable and Lipschitz condition with respect to the second variable.
, and all its r-th
order partial derivatives fulfill the generalized
Hölder conditions with respect to
the first variable and Lipschitz condition with respect to the second variable.
Define, by recurrence,
functions ![]() as follows:
as follows:
|
|
Before formulating the main results of our paper, we will need the following two lemmas.
Lemma 2.1 ([6],
Lemma 1). If the assumption (i) is fulfilled, then the functions ![]() ,
, ![]() defined by (4), are
defined by (4), are ![]() -times continuously
differentiable in
-times continuously
differentiable in ![]() and, for
and, for ![]() , we have
, we have
|
|
where
|
|
and ![]() is a polynomial of the
variables
is a polynomial of the
variables ![]() whose coefficients are
functions of the variables
whose coefficients are
functions of the variables ![]() and are of the class
and are of the class ![]() with
respect to
with
respect to ![]() and
and ![]() .
.
Lemma 2.2 ([6],
Lemma 2). If the assumption (i) is fulfilled, ![]() and
and
then the derivatives of ![]() fulfil the following system of equations:
fulfil the following system of equations:
and ![]()
3. Main results
Theorem 3.1. Let
![]() be fixed and let a function
be fixed and let a function ![]() be such that for any
be such that for any ![]() the function
the function ![]() is r-times differentiable and its r-th derivatives satisfy the
Lipschitz condition on
is r-times differentiable and its r-th derivatives satisfy the
Lipschitz condition on ![]() If the composition
operator H of the generator h maps the space
If the composition
operator H of the generator h maps the space ![]() into
into ![]() and satisfies the inequality
and satisfies the inequality
| (6) |
for some function ![]() then there exist
then there exist ![]() and
and
![]() such that
such that
Proof. For
every fixed ![]() the function
the function ![]() ,
, ![]() , as a constant,
is
, as a constant,
is ![]() -times differentiable
and its n-th derivatives satisfy the generalized Hölder condition, so,
by assumption,
-times differentiable
and its n-th derivatives satisfy the generalized Hölder condition, so,
by assumption, ![]() Thus, taking into
account the assumption, it follows that the function h fulfils (i).
Thus, taking into
account the assumption, it follows that the function h fulfils (i).
Let us fix ![]() and define the
function
and define the
function
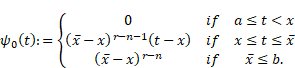 |
It is obvious that ![]() with the constant
with the constant ![]() , so, by
Remark 1,
, so, by
Remark 1, ![]() satisfy the generalized Hölder condition with the constant
satisfy the generalized Hölder condition with the constant
Let us take arbitrary ![]() ,
, ![]() . Putting
. Putting
|
|
we get
|
|
and
| (9) |
for all ![]()
Hence, ![]() ,
, ![]() , and, by the
definition of the function
, and, by the
definition of the function ![]() ,
for all
,
for all ![]() , we obtain
, we obtain
| (10) |
and
| (11) |
Since, by (8),
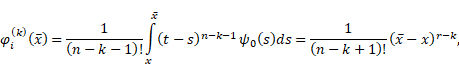
|
and, by (9),
therefore
|
|
Setting ![]() , where
, where ![]() are defined in Lemma
1, inequality (6) has
the following form
are defined in Lemma
1, inequality (6) has
the following form
|
|
|
|
||
|
for all ![]()
Omitting the sign supremum on the left hand side
of the above inequality and
putting ![]() , by (10), (11), we get
, by (10), (11), we get
|
|
|
|
|
|
and, consequently,
|
|
|
|
|
|
Hence, letting ![]() in so obtained
inequality, by the right-hand side continuity
in zero of
in so obtained
inequality, by the right-hand side continuity
in zero of ![]() and (12), we have
and (12), we have
whence,
Thus ![]() is linear with respect
to the second variable and, consequently, there exist functions
is linear with respect
to the second variable and, consequently, there exist functions ![]()
![]() such that
such that
| (13) |
Since ![]() for all
for all ![]() (13),
(13),
therefore ![]() , which completes the
proof.
, which completes the
proof.
In the sequel the following definition plays a crucial role:
Definition 3.1 ([10], Definition 1). Let ![]() and
and ![]() be two metric spaces. We say that a mapping
be two metric spaces. We say that a mapping ![]() is uniformly bounded if, for any
is uniformly bounded if, for any![]() , there exists a real number
, there exists a real number ![]() such that for any
nonempty set
such that for any
nonempty set ![]() , we have
, we have
The main result of this paper reads as follows:
Theorem 3.2.
Let ![]() be fixed and let a
function
be fixed and let a
function ![]() be such that for any
be such that for any ![]() the function
the function ![]() is
r-times differentiable
and its r-th derivatives satisfy the Lipschitz condition on
is
r-times differentiable
and its r-th derivatives satisfy the Lipschitz condition on ![]() If the composition operator
If the composition operator ![]() of the generator
of the generator ![]() maps the space
maps the space ![]() into
into ![]() and is uniformly
bounded, then there exist
and is uniformly
bounded, then there exist ![]() and
and ![]() such that
such that
and
Proof. Take
any ![]() and arbitrary
and arbitrary ![]() such that
such that
Since ![]() by the uniform
boundedness of
by the uniform
boundedness of ![]() , we have,
, we have,
that is
and the result follows from Theorem 1.
Remark 3.1. If
the function ![]() in Definition 3.1 is
right continuous at
in Definition 3.1 is
right continuous at ![]() and
and ![]() (or if only
(or if only ![]() ), then, clearly, the
uniform boundedness of the involved operator reduces to its uniform continuity.
), then, clearly, the
uniform boundedness of the involved operator reduces to its uniform continuity.
Remark 3.2. Taking
in Theorem 3.2 ![]()
![]() such that
such that ![]() is
finite,
is
finite, ![]() , for some constant
, for some constant ![]() , we get the main
result of Knop [5].
, we get the main
result of Knop [5].
Remark 3.3.
Theorem 3.2 also extends the result of Lupa [6], where ![]()
![]() is such that
is such that ![]() (0)
(0) ![]() ,
, ![]() (
(![]() and
and ![]() .
.
4. Conclusions
We show that if a Nemytskij
composition operator ![]() mapping the space
mapping the space ![]() of
of ![]() -times differentiable functions with the
-times differentiable functions with the ![]() -th derivative satisfying
a generalized Hölder condition into
-th derivative satisfying
a generalized Hölder condition into
![]() is uniformly bounded or
uniformly continuous, then its generator
is an affine function with respect to the second variable. This significantly
extends the result of [5, 6] where much stronger Lipschitz norm continuity
of
is uniformly bounded or
uniformly continuous, then its generator
is an affine function with respect to the second variable. This significantly
extends the result of [5, 6] where much stronger Lipschitz norm continuity
of ![]() is assumed.
is assumed.
References
[1] Krämer R., Mathé P., Modulus of continuity of Nemytskii operators with application to the problem of option pricing, Journal of Inverse and Ill-posed Problems 2008, 16(5), 435-461.
[2] Matkowski J., Functional equation and Nemytskij operators, Funkcial Ekv. 1982, 25, 127-132.
[3] Appell J., Banaś J., Merentes N., Bounded Variation and Around, De Gruyter Studies in Non- linear Analysis and Applications, Volume 17, Würzburg 2014.
[4] Appell J., Zabrejko P.P., Nonlinear Superposition Operators, Cambridge University Press, Cambridge-New York-Port Chester-Melbourne-Sydney 1990.
[5] Knop J., On globally Lipschitzian Nemytskii operator in a special Banach space of functions, Fasciculi Mathematici 1990, 280(21), 79-85.
[6] Lupa M., Form of Lipschitzian operator of substitution in some class of functions, Zeszyty Naukowe Politechniki Łódzkiej 1990, Matematyka, 21, 87-96.
[7] Matkowski J., Miś J., On a characterization of Lipschitzian operators of substitution in the space BV[a,b], Math. Nachr. 1984, 117, 155-159.
[8] Matkowski J., Uniformly continuous superposition operators in the space of Hölder functions, J. Math. Anal. App. 2009, 359, 56-61.
[9] Matkowski J., Uniformly continuous superposition operators in the spaces of bounded variation functions, Math. Nach. 2010, 283(7), 1060-1064.
[10] Matkowski J., Uniformly bounded composition operators between general Lipschitz functions normed spaces, Topol. Methods Nonlinear Anal. 2011, 38(2), 395-406.
[11] Matkowski J., Wróbel M., Uniformly bounded set-valued Nemytskij operators acting between generalized Hölder function spaces, Cent. Eur. J. Math. 2012, 10(2), 609-618.
[12] Wróbel M., Uniformly bounded Nemytskij operators between the Banach spaces of functions of bounded n-th variation, J. Math. Anal. Appl. 2012, 391, 451-456.