Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Majchrzak_2018,
   doi = {10.17512/jamcm.2018.2.04},
   url = {https://doi.org/10.17512/jamcm.2018.2.04},
   year = 2018,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {17},
   number = {2},
   pages = {43--50},
   author = {Ewa Majchrzak and  Bohdan Mochnacki},
   title = {Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2018.2.04
UR  - https://doi.org/10.17512/jamcm.2018.2.04
TI  - Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Majchrzak, Ewa
AU  - Mochnacki, Bohdan
PY  - 2018
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 43
EP  - 50
IS  - 2
VL  - 17
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Majchrzak, E., & Mochnacki, B. (2018). Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works. Journal of Applied Mathematics and Computational Mechanics, 17(2), 43-50. doi:10.17512/jamcm.2018.2.04

Majchrzak, E. & Mochnacki, B., 2018. Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works. Journal of Applied Mathematics and Computational Mechanics, 17(2), pp.43-50. Available at: https://doi.org/10.17512/jamcm.2018.2.04

[1]E. Majchrzak and B. Mochnacki, "Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 2, pp. 43-50, 2018.

Majchrzak, Ewa, and Bohdan Mochnacki. "Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works." Journal of Applied Mathematics and Computational Mechanics 17.2 (2018): 43-50. CrossRef. Web.

1. Majchrzak E, Mochnacki B. Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(2):43-50. Available from: https://doi.org/10.17512/jamcm.2018.2.04

Majchrzak, Ewa, and Bohdan Mochnacki. "Application of numerical methods for solving the non-fourier equations. A review of our own and collaborators’ works." Journal of Applied Mathematics and Computational Mechanics 17, no. 2 (2018): 43-50. doi:10.17512/jamcm.2018.2.04

APPLICATION OF NUMERICAL METHODS FOR SOLVING THE NON-FOURIER EQUATIONS. A REVIEW OF OUR OWN AND COLLABORATORS’ WORKS

Ewa Majchrzak ¹, Bohdan Mochnacki ²

¹ Institute of Computational Mechanics and Engineering, Silesian University of Technology
Gliwice, Poland
² University of Occupational Safety Management in Katowice,
Katowice, Poland
ewa.majchrzak@polsl.pl, bmochnacki@wszop.edu.pl

Received: 16 May 2018; Accepted: 20 June 2018

Abstract. Thermal processes occuring in the solid bodies are, as a rule, described by the well-known Fourier equation (or the system of these equations) supplemented by the appropriate boundary and initial conditions. Such a mathematical model is sufficiently exact to describe the heat transfer processes in the macro scale for the typical materials. It turned out that the energy equation based on the Fourier law has the limitations and it should not be used in the case of the microscale heat transfer and also in the case of materials with a special inner structure (e.g. biological tissue). The better approximation of the real thermal processes assure the modifications of the energy equation, in particular the models in which the so-called lag times are introduced. The article presented is devoted to the numerical aspects of solving these types of equations (in the scope of the microscale heat transfer). The results published by the other authors can be found in the references posted in the works cited below.

MSC 2010: 35L10, 65M06

Keywords: heat transfer, non-Fourier heat diffusion models, numerical methods, computational mechanics

1. Governing equations

In the well-known Fourier law, the relationship between the heat flux and the temperature gradient for the heat conduction process is of the form

(1)

where q is a heat flux vector, λ is a thermal conductivity, T, X, t denote the temperature, spatial co-ordinates and time.

To take into account the finite velocity of thermal wave dissipation, the following modification of the last formula has been proposed

(2)

where τ_q [s] is the positive constant called the relaxation time. The generalization of the Fourier law presented above leads to the Cattaneo-Vernotte equation. The more overall approach results from the formula

(3)

in which the additional parameter τ_T [s] called the thermalization time appears. As will be shown, the acceptation of equation (3) leads to the heat conduction model called the dual phase lag equation (DPLE). The Cattaneo-Vernotte equation is, of course, the simplified form of DPLE.

To obtain the DPLE one develops the left and right sides of equation (3) into the Taylor series

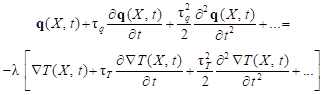(4)

Taking into account the components containing the first derivatives and using the known diffusion equation

(5)

where c is a volumetric specific heat, Q is a volumetric internal heat source capacity, one obtains

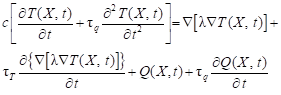(6)

Equation (6) corresponds to the most popular form of DPLE.

The more complex form of DPLE is associated with the introduction of the second-order derivatives, and then

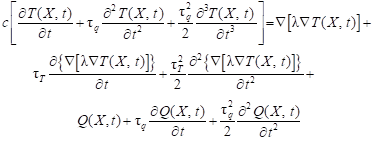(7)

In literature, equation (7) is called the second order DPLE. In the practical applications, the constant values of thermophysical parameters are (as a rule) assumed and then in the case of the second order DPLE one has

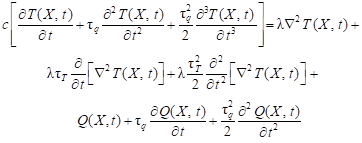(8)

It should be pointed out, that the ‘mixed’ variants of the first and the second order of DPLE can be also considered.

The equation considered must be supplemented with the boundary conditions. The form of these conditions is different than the typical ones appearing in the classical macro models (this element is often neglected, leading to the adoption of the incorrect theoretical model of the process and as a consequence to the incorrect results). For example, the well known Neumann condition takes the form

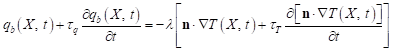(9)

or (for the second order model)

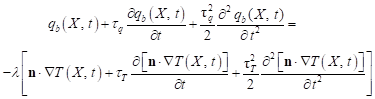(10)

where q_b(X, t) is a given boundary heat flux, while denotes a normal derivative.

The initial conditions are also given, in particular

(11)

Additionally for the second order DPLE

(12)

where T_p is an initial temperature, u(X) and v(X) are the known functions.

2. Microscale heat transfer, 1D and 2D problems

One of the physical processes in which the dual phase lag model should be applied is the microscale heat transfer. Generally speaking, the differences between the macroscopic heat conduction described by the Fourier equation and the models concerning the typical thermal interactions in the microscale result from the extremely short duration of the process, extreme temperature gradients and geometrical features of the domain considered. So, the introduction of the lag times becomes necessary. The typical problem for which the DPLE is applied are the ultrafast laser pulse interactions with homogeneous or non-homogeneous thin metal films. Thermal interactions in the system considered are of the vital importance in microtechnology applications, and it is a reason that the problems connected with fast heating of solids have become a very active research area.

Some important problems in this area can be solved using the analytical methods. At this point, one may quote paper [1] in which the thin metal film subjected to the laser heating is considered. The laser action is taken into account by the introduction of the artificial internal heat source in the film domain. At the same time, on the external surfaces of the system, the no-flux boundary conditions have been assumed.

A part of the problems related to the DPLE applications have been solved using the explicit scheme of the finite difference method. As one knows, a stability condition should be formulated for these types of algorithms. The considerations concerning the formulation of the condition discussed are presented in [2] and [3]. The implicit scheme of the FDM was also the topic of our research work, here the papers [4, 5] should be mentioned.

In the work [5] cited above, both the first and the second order DPLE have been considered. In particular, the heat transfer processes proceeding in the metal film (gold) subjected to the ultra-fast laser pulse have been analyzed. The laser action is taken into account by the introduction of an internal heat source to the domain interior. The capacity of this source is given by the formula

(13)

where I₀ is the laser intensity, t_p is the characteristic time of laser pulse, δ is the optical penetration depth, R is the reflectivity of the irradiated surface and β = 4 ln2.

The thin metal film (L = 100 nm) made of gold has been considered. The surface x = 0 of the domain is subjected to the laser pulse. The parameters determining the capacity of the internal heat source (equation (13)) are equal to I₀ = 13.7 J/m², t_p = 0.1 ps, δ = 15.3 nm, R = 0.93. The initial temperature of domain equals T₀ = 300 K, while the initial values of functions u(x) = 0, v(x) = 0. Differential mesh parameters: n = 1000 (number of nodes), ∆t = 0.0001 ps (time step). Thermo- physical parameters of material are collected in [5].

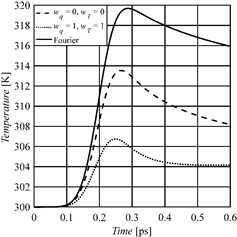
Fig. 1. Temperature history at the irradiated surface for different models (gold)

In Figure 1, the results of numerical computations are shown. The values w_q = w_T = 0 correspond to the first order DPLE, while w_q = w_T = 1 correspond to the second order DPLE. The solution resulting from the Fourier model is also marked. One can see that the differences between solutions are clearly visible.

At the stage of numerical modeling based on the FDM, apart from the explicit and implicit schemes, the intermediate variants have been also used [6] (the Crank--Nicholson method). In turn, in work [7] the axially-symmetrical task (2D problem - as shown in Figure 2) have been solved using the alternating direction implicit method. The efficiency of the laser beam can be described by the time-dependent bell-type function. The capacity of internal heat sources resulting from the laser action is consequently also described by the axially symmetrical function, in particular

(14)

where

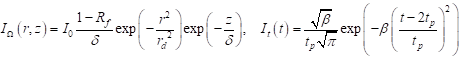(15)

The denotations are the same as in formula (13).

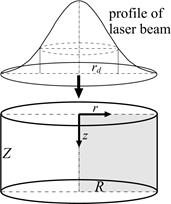
Fig. 2. Cylindrical micro-domain

So, it seems that for the formulation of the similar problems the cylindrical co-ordinate system is the most beneficial.

The applications of DPLE in the scope of the microscale heat transfer for the multi-layered domains have been also the subject of our team research. Here the papers [8-10] can be quoted. In particular, the work [10] deserves special mention. The authors present the correct version of the ideal contact boundary condition and the numerical algorithm in which this condition is applied. Thus

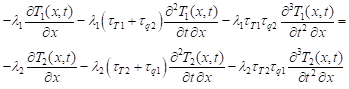(16)

and additionally T₁(x, t) = T₂(x, t). Indexes 1 and 2 correspond to domains being in the thermal contact.

In the majority of papers concerning the heterogeneous domains, the condition (16) is considered in the classical form, meaning under the assumption that τ_q = τ_T = 0. Such a solution can be affected with the big error.

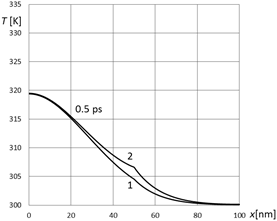
Fig. 3. Temperature distribution for 0.5 ps (1 - DPL model, 2 - DPL with the macroscopic boundary conditions) [10]

Figure 3 taken from [10] shows the differences between solutions (temperature profile for time 0.5 ps, while x = 50 nm corresponds to the internal boundary). The differences are clearly visible.

Here one should also mention the papers [11] and [12]. In [11] the DPLE for the axially-symmetrical domain has been solved using the generalized finite difference method, while in [12] the solution of the 1D problem has been found on the basis of the boundary element method. The interaction of the laser with high efficiency may cause a change of state of the metal layer (melting or even ablation). As an example of the DPLE model taking into account these phenomena the paper [13] can be mentioned.

3. Conclusions

The review presented above concerns (with a few exceptions) the papers that have been published after 2015. The problems discussed are connected with the realization of the research problem sponsored by NSC and conducted by Ewa Majchrzak. As part of the project, the research concerning the non-Fourier models in the scope of bio-heat transfer are also carried out. The examples of the problems considered can be found in [14-17].

Acknowledgement

The paper and research are financed within the project 2015/19/B/ST8/01101 sponsored by National Science Centre (Poland).

References

[1] Ciesielski, M. (2017). Analytical solution of the dual phase lag equation describing the laser heating of thin metal film. Journal of Applied Mathematics and Computational Mechanics, 16(1), 33-40.

[2] Majchrzak, E., & Mochnacki, B. (2016). Dual-phase lag equation. Stability conditions of a numerical algorithm based on the explicit scheme of the finite difference method. Journal of Applied Mathematics and Computational Mechanics, 15(3), 89-96.

[3] Mochnacki, B., & Tuzikiewicz, W. (2016). Cattaneo-Vernotte bioheat transfer equation. Stability conditions of numerical algorithm based on the explicit scheme of the finite difference method. Journal of Applied Mathematics and Computational Mechanics, 15(4), 137-144.

[4] Majchrzak, E., & Mochnacki, B. (2017). Implicit scheme of the finite difference method for 1D dual-phase lag equation. Journal of Applied Mathematics and Computational Mechanics, 16(3), 37-46.

[5] Majchrzak, E., & Mochnacki, B. (2018). Implicit scheme of the finite difference method for the second-order dual phase lag equation. Journal of Theoretical and Applied Mechanics, 56(2), 393-402.

[6] Mochnacki, B., & Ciesielski, M. (2017). Numerical solution of the dual phase lag equation using the control volume method and Crank-Nicolson scheme. ECCOMAS MSF Thematic Conference, Ljubljana, Slovenia, 196-199.

[7] Ciesielski, M. (2017). Application of the alternating direction implicit method for numerical solution od the dual phase lag equation. Journal of Theoretical and Applied Mechanics, 55(3), 839-852.

[8] Majchrzak, E., Mochnacki, B., & Suchy, J.S. (2009). Numerical simulation of thermal processes proceeding in a multi-layered film subjected to ultrafast laser heating. Journal of Theoretical and Applied Mechanics, 47(2), 383-396.

[9] Majchrzak, E., Mochnacki, B., Greer, A.L., & Suchy, J.S. (2009). Numerical modeling of short pulse laser interactions with multi-layered thin metal films. Computer Modeling in Engineering and Sciences, 41, 2, 131-146.

[10] Majchrzak, E., & Kałuża, G. (2017). Analysis of thermal processes occurring in the heated multilayered metal films using the dual-phase lag model. Archives of Mechanics, 69, 4-5, 275-287.

[11] Turchan, Ł. (2017). Solving the dual-phase lag bioheat transfer equation by the generalized finite difference method. Archives of Mechanics, 69, 4-5, 389-407.

[12] Majchrzak, E., & Mochnacki, B. (2017). Numerical model of thin metal film heating using the boundary element method. Computer Methods in Materials Science, 17, 1, 12-17.

[13] Mochnacki, B., & Ciesielski, M. (2016). Dual phase lag model of melting process in domain of metal film subjected to an external heat flux. Archives of Foundry Engineering, 16, 4, 85-90.

[14] Ciesielski, M., Duda, M., & Mochnacki, B. (2016). Comparison of bio-heat transfer numerical models based on the Pennes and Cattaneo-Vernotte equations. Journal of Applied Mathematics and Computational Mechanics, 15, 4, 33-38.

[15] Mochnacki, B., & Majchrzak, E. (2017). Numerical model of thermal interactions between cylindrical cryoprobe and biological tissue using the dual-phase lag equation. International Journal of Heat and Mass Transfer, 108, 1-10.

[16] Kałuża, G., Majchrzak, E., & Turchan Ł. (2017). Sensitivity analysis of temperature field in the heated soft tissue with respect to the perturbations of porosity. Applied Mathematical Modelling, 49, 498-513.

[17] Majchrzak, E., Jasiński, M., & Turchan Ł. (2017). Modeling of laser-soft tissue interactions using the dual-phase lag equation: sensitivity analysis with respect to selected tissue parameters. Defect and Diffusion Forum, 379, 108-123.