Application of HM-networks with unreliable systems for finding the memory capacity in the information systems
Mikhail Matalytski
,Pawel Zajac
,Dmitry Kopats
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Matalytski_2018,
doi = {10.17512/jamcm.2018.2.05},
url = {https://doi.org/10.17512/jamcm.2018.2.05},
year = 2018,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {17},
number = {2},
pages = {51--63},
author = {Mikhail Matalytski and Pawel Zajac and Dmitry Kopats},
title = {Application of HM-networks with unreliable systems for finding the memory capacity in the information systems},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2018.2.05 UR - https://doi.org/10.17512/jamcm.2018.2.05 TI - Application of HM-networks with unreliable systems for finding the memory capacity in the information systems T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Matalytski, Mikhail AU - Zajac, Pawel AU - Kopats, Dmitry PY - 2018 PB - The Publishing Office of Czestochowa University of Technology SP - 51 EP - 63 IS - 2 VL - 17 SN - 2299-9965 SN - 2353-0588 ER -
Matalytski, M., Zajac, P., & Kopats, D. (2018). Application of HM-networks with unreliable systems for finding the memory capacity in the information systems. Journal of Applied Mathematics and Computational Mechanics, 17(2), 51-63. doi:10.17512/jamcm.2018.2.05
Matalytski, M., Zajac, P. & Kopats, D., 2018. Application of HM-networks with unreliable systems for finding the memory capacity in the information systems. Journal of Applied Mathematics and Computational Mechanics, 17(2), pp.51-63. Available at: https://doi.org/10.17512/jamcm.2018.2.05
[1]M. Matalytski, P. Zajac and D. Kopats, "Application of HM-networks with unreliable systems for finding the memory capacity in the information systems," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 2, pp. 51-63, 2018.
Matalytski, Mikhail, Pawel Zajac, and Dmitry Kopats. "Application of HM-networks with unreliable systems for finding the memory capacity in the information systems." Journal of Applied Mathematics and Computational Mechanics 17.2 (2018): 51-63. CrossRef. Web.
1. Matalytski M, Zajac P, Kopats D. Application of HM-networks with unreliable systems for finding the memory capacity in the information systems. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(2):51-63. Available from: https://doi.org/10.17512/jamcm.2018.2.05
Matalytski, Mikhail, Pawel Zajac, and Dmitry Kopats. "Application of HM-networks with unreliable systems for finding the memory capacity in the information systems." Journal of Applied Mathematics and Computational Mechanics 17, no. 2 (2018): 51-63. doi:10.17512/jamcm.2018.2.05
APPLICATION OF HM-NETWORKS WITH UNRELIABLE SYSTEMS FOR FINDING THE MEMORY CAPACITY IN THE INFORMATION SYSTEMS
Mikhail Matalytski 1, Pawel Zajac 2, Dmitry Kopats 3
1,2 Institute
of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
3 Faculty of Mathematics and Computer Science, Grodno State
University
Grodno, Belarus
m.matalytski@gmail.com, pawel_zajac@vp.pl, dk80395@mail.ru
Received: 13 November 2017; Accepted: 22 May 2018
Abstract. To solve the problem of determining the memory capacity of the information systems (IS), it was proposed to use a stochastic model, based on the use of HM (Howard- -Matalytski) - queueing networks with incomes. This model takes into account the servicing of requests along with their volumes, the ability to change the volumes of the requests over time and the possibility of damaging IS nodes and their repairs, so servicing of demands can be interrupted randomly. The expressions are generated for the mean (expected) values of total requests volumes in the IS nodes.
MSC 2010: 60K20, 60K25, 68M20, 90B22
Keywords: HM-network, information systems, unreliable service, volumes of requests
1. Introduction
In IS, the total volume of memory is limited to a certain value, which is usually called memory capacity [1]. When designing systems, the main task is to find the expected volume of memory to take into account the conditions that limit the share of lost information. One of the methods for solving problems of IS design is the use of HM-queueing networks (QN) [2]. According to IS, we will continue to understand systems as information transformation objects, delivered in the form of messages (requests) [1]. HM-networks can be used to determine the volume of a buffer storage of systems that are representing processing IS nodes and transferring demands. Note that this problem is crucial, for example in the design of hubs or communication centers in information networks. The following model can also be used to solve an important problem that recently appeared in the IS, i.e., the problem of excessive buffering (the problem of determining the required memory volume) [3]. Bufferbloat - a phenomenon that occurs in packet communication networks, when the buffering causes an excessive increase in the time of the packets and packet delay variation, and the resulting decrease in the throughput volume of IS.
Neglect time dependence of requests processing of their volumes can lead to serious errors in finding the buffer memory in IS. The solution in the general case of the above problems can be based on the use of HM-networks with incomes. In such networks, the request during the transition from one queueing system (QS) to another brings some income last (which is equal to the volume of this request), and the income (volume) of the first QS is reduced by this amount.
Note that the method of finding non-stationary probabilities of states and finding average network characteristics with systems of medium unreliable network systems, operating under high load with the help of multidimensional generating functions are described in the monograph [4], the HM-network with unreliable service [4, 5]. For the first time, the use of HM-networks to estimate the volume in IS has been described in [6]. In [7, 8], a proposed method of finding the expected volume of homogeneous requests in open network systems with limited waiting times in queues systems, and in [9] - in the HM-network with limited sojourn times of requests.
2. Finding the expected volumes of requests in the case, when is known only first moments other incomes the transitions between the network states
Let’s look at QN with unreliable QS. Suppose S0
handles are reliable, and in other systems S1,...,Sn lines can be damaged. The state of the system Si is described by the vector ![]() , where
, where ![]() are the number of requests and
undamaged lines in the system Si at time t, respectively,
are the number of requests and
undamaged lines in the system Si at time t, respectively, ![]() Next, let’s specify the
Next, let’s specify the ![]() vector as the state of the network.
Assume that the servicing times, the line operating times, and line
repair times are independent random variables (RV). The servicing time for IS
requests has an exponential distribution with a parameter
vector as the state of the network.
Assume that the servicing times, the line operating times, and line
repair times are independent random variables (RV). The servicing time for IS
requests has an exponential distribution with a parameter ![]() ; the operation time of each line
without damage in this system has an exponential distribution with the parameter
; the operation time of each line
without damage in this system has an exponential distribution with the parameter ![]() After the damage of the line immediately
begins repairing it, the repair time also has an exponential
distribution with the
parameter
After the damage of the line immediately
begins repairing it, the repair time also has an exponential
distribution with the
parameter ![]() . Assume that if the line receives a damage while servicing
the call, the request servicing will continue after the line has been
repaired. We assume that the discipline of servicing requests in all systems is
FIFO. Then at the time interval
. Assume that if the line receives a damage while servicing
the call, the request servicing will continue after the line has been
repaired. We assume that the discipline of servicing requests in all systems is
FIFO. Then at the time interval ![]() , the request can be handled on every
line of the system Si with
the probability
, the request can be handled on every
line of the system Si with
the probability ![]() , the line with
the probability
, the line with
the probability ![]() may be damaged or corrected with
the probability
may be damaged or corrected with
the probability ![]() Let us denote by pij - the probability of
passing
the request after serving in the Si system to the Sj system,
Let us denote by pij - the probability of
passing
the request after serving in the Si system to the Sj system, ![]() matrix
is a matrix of transition probabilities of the irreducible Markov chain.
matrix
is a matrix of transition probabilities of the irreducible Markov chain.
Let’s look at the dynamics of the change in
the expected volume of requests
in some Si network
systems. Let ![]() be the volume at time t, and at
the beginning of time the system has the volume
be the volume at time t, and at
the beginning of time the system has the volume ![]() Then
this volume at the given QS
at time Δt can be expressed by the formula
Then
this volume at the given QS
at time Δt can be expressed by the formula
| (1) |
where ![]() - a change in the
volume of requests in the system Si in the time interval
- a change in the
volume of requests in the system Si in the time interval ![]() . To find this value,
you need to find the probabilities of events that may occur at time
. To find this value,
you need to find the probabilities of events that may occur at time ![]() and volume changes in
the Si system
associated with
these events.
and volume changes in
the Si system
associated with
these events.
1. With probability
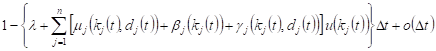 |
in the time interval ![]() the change in system state Si will not take place, the
volume of requests in that system increases by
the change in system state Si will not take place, the
volume of requests in that system increases by ![]() ,
where
,
where ![]() ,
, ![]() .
.
2. With
probability ![]() a request after servicing
in Si , goes to the external environment, the volume of requests in system
Si
decreases by the value of
a request after servicing
in Si , goes to the external environment, the volume of requests in system
Si
decreases by the value of ![]() , where
, where ![]() ,
, ![]() .
.
3. With
probability ![]() , a request from the outside environment
enters the system Si and
increases the volume of requests to the size
, a request from the outside environment
enters the system Si and
increases the volume of requests to the size ![]() ,
, ![]() ,
, ![]() .
.
4. With
probability ![]() a request, after servicing
in the Si system,
goes to the system Sj ; the volume of requests in system Si changes by the value
a request, after servicing
in the Si system,
goes to the system Sj ; the volume of requests in system Si changes by the value ![]() , where
, where ![]() ,
, ![]() ,
, ![]() .
.
5. With
probability ![]() a request, after servicing
in system Sj goes
to the system Si ; the total volume of requests in the system Si will increase by the
value of
a request, after servicing
in system Sj goes
to the system Si ; the total volume of requests in the system Si will increase by the
value of ![]() , where
, where ![]() ,
, ![]() ,
, ![]() .
.
6. With
probability ![]() a number of active lines in system Sj decreases by 1, the
volume of requests in the system Si will increase by
the value
a number of active lines in system Sj decreases by 1, the
volume of requests in the system Si will increase by
the value ![]() ,
, ![]() .
.
The following cases are possible.
7. The number of operating lines in the system Sj will decrease by 1, the
request after servicing in the system Si will go to the external environment, ![]() .
.
8. The service line in the system Sj is damaged, the request enters the
system Si from
the outside environment, ![]() .
.
9. The number of service lines in the system Ss will be reduced by 1,
the request after servicing in the system Si will go to the system Sj, ![]() ,
,
![]() .
.
10. The number of service lines in the system Ss will decrease by 1, the
request
after servicing in the system Sj will go to Si, ![]() ,
, ![]() .
.
The probabilities of the corresponding events
in cases 7-10 are equal ![]() , for example, in
case 7 for this probability we have
, for example, in
case 7 for this probability we have
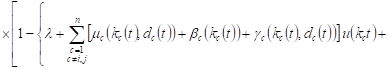
|
Changes in the volume of expected requests in the system Si :
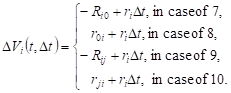 |
11. With probability ![]() , a number of
service lines
in system Sj will
increase by 1, and the total volume of requests in the system Si by
, a number of
service lines
in system Sj will
increase by 1, and the total volume of requests in the system Si by ![]() ,
, ![]() ,
, ![]() .
.
12. With probability ![]() one line of service
is being
repaired in the system Si , the total volume of applications will decrease by
one line of service
is being
repaired in the system Si , the total volume of applications will decrease by ![]() , where
, where ![]() ,
, ![]() - RV with distribution function
- RV with distribution function ![]() - repair fee for the service line in
the system Si ,
- repair fee for the service line in
the system Si ,![]() .
.
In addition, the following cases are possible.
13. There will be a repair of the service line in the system, the
request after servicing in the system Sj will go to the external environment; ![]() ,
, ![]() .
.
14. The service line
will be repaired in the system Si , system
Si will go
to the
outside environment; ![]() .
.
15. The service line
will be repaired in the system Sj , the system ![]() enters a request from
the outside environment;
enters a request from
the outside environment; ![]()
![]() .
.
16. There will be
repair of the service line in the system Si , and in
this system
is entering a request from the outside environment, ![]() .
.
17. There will be
repair of the service line in the system Ss , the
request after
servicing in the system Si will
go to system Sj , ![]() ,
, ![]() ,
, ![]() .
.
18. The system Si will repair the service
line, the request after the servicing system goes to Sj , ![]() ,
, ![]() .
.
19. There will be
repair of the service line in the system Ss , the
request after servicing system Sj goes to Si , ![]() ,
, ![]() ,
, ![]() .
.
20. There will be
repair of the service line in the system Si , the
request after
the servicing system Sj goes
to Si , ![]() ,
, ![]() .
.
21. The system Sc will repair the service
line, the system will be damaged and
the status of the other QS will not change,![]() ,
, ![]() .
.
22. The service line
will be repaired in the system Si , the
service line will be
damaged in the system Ss and
will not change states of other QS, ![]() .
.
The probabilities of events taking place in
13-22 cases will be equal ![]() ,
because, for example, in case 13 we will have
,
because, for example, in case 13 we will have
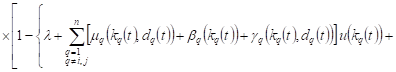
|
Changes in the expected volume of requests in the system Si in cases 13-22 are as follows:
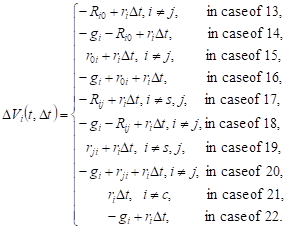 |
The following cases are possible:
23. The service line will be repaired in the system Sc , the service line will be
damaged in the system Ss , will not change states of other QS, and after the
operation in the system will go to the outside environment, ![]() ,
, ![]() .
.
24. The service line will be repaired in the system Si , the service line will be
damaged in the system Ss , the request after servicing system goes to the outside
environment, ![]() .
.
25. The service line will be repaired in the system Sc , the service line will be
damaged in the system Ss , the request goes into the ![]() system
from the outside environment,
system
from the outside environment, ![]() ,
, ![]() .
.
26. The service line will be repaired in the system Si , the service line will be
damaged in the system Ss , the request goes into the Si system from the outside environments, ![]() .
.
27. The service line will be repaired in the system Sc , the service line will be
damaged in the system Ss , the request after servicing in system Si goes into
the Sj , ![]() ,
, ![]() ,
, ![]() .
.
28. The service line will be repaired in the system Si , the service line will be
damaged in the system Ss , the request after servicing in system Ss goes into
the Sj , ![]() ,
, ![]() .
.
29. The service line will be repaired in the system Sc , the service line will be damaged in the system Ss , the request after servicing in system Sj goes into the Si , ![]() ,
, ![]() ,
, ![]() .
.
30. The service line will be repaired in the system Si and the service line
will be damaged in the system Ss . The
request after servicing in system goes into
the Si , ![]() ,
, ![]() .
.
In appropriate cases, the probability of
23-30 events are equal ![]() For
example, in case 23, the probability will be equal
For
example, in case 23, the probability will be equal
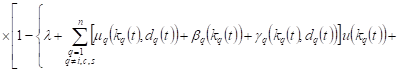
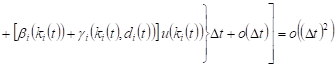 . . |
We will assume that RV ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , are independent,
, are independent, ![]() ,
, ![]() . The
changes of the volumes of requests in the system Si in cases 23-30 are equal
to:
. The
changes of the volumes of requests in the system Si in cases 23-30 are equal
to:
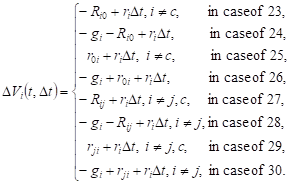 |
With constant execution of the process ![]() with
with ![]() can
be written
can
be written
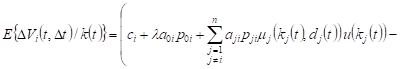
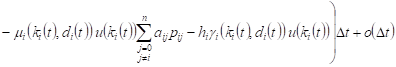 , , |
Averaging after ![]() ,
taking into account the condition of normalization
,
taking into account the condition of normalization ![]() , we will obtain the change in the expected volume
of the system Si
, we will obtain the change in the expected volume
of the system Si
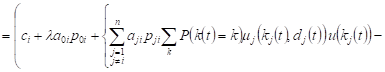
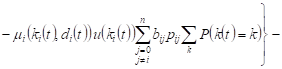
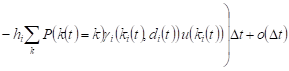 , , |
Let the system Si at the time t
have ![]() ,
, ![]() . In
each of them,
the servicing time, the work time and the repair time of damaged lines have
an exponential distribution with
parameters,
. In
each of them,
the servicing time, the work time and the repair time of damaged lines have
an exponential distribution with
parameters, ![]() ,
, ![]() and
and ![]() respectively,
respectively, ![]() . Assume that the intensity of
request servicing and the intensity of repair of
damaged lines in the system Si depends linearly on the
number of requests and
the number of damaged lines.
. Assume that the intensity of
request servicing and the intensity of repair of
damaged lines in the system Si depends linearly on the
number of requests and
the number of damaged lines.
We will also assume that the averaging of the expression
of ![]() is
is ![]() , i.e.
, i.e. ![]() .
.
In addition, ![]() ,
where
,
where ![]() ,
, ![]() respectively
mean
the number of requests (waiting and servicing) and the average number of lines
operating in the system Si at
the time t,
respectively
mean
the number of requests (waiting and servicing) and the average number of lines
operating in the system Si at
the time t, ![]() . Given these assumptions, we obtain
the approximate
. Given these assumptions, we obtain
the approximate
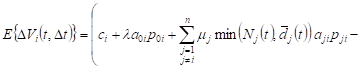
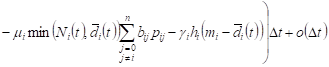 . . | (2) |
Because the operating times and repair lines in
the system Si have
an exponential distribution, ![]() - the average
number of service lines repaired over time
- the average
number of service lines repaired over time ![]() in the system Si ,
in the system Si , ![]() - the average number of service lines
in the system Si damaged over time
- the average number of service lines
in the system Si damaged over time ![]() ,
, ![]() .
Therefore
.
Therefore ![]() ,
,
![]() , where
, where ![]() , we get a linear differential equation
, we get a linear differential equation ![]() ,
,
![]() , and with the initial condition
, and with the initial condition ![]() we have:
we have:
| (3) |
The equation for the average number of requests in the QS network has the form
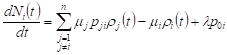 , , | (4) |
It is moved in the same way as in [4] for
networks with another feature.
The average number of occupied service lines ![]() in
the system Si can
be
approximated by an expression
in
the system Si can
be
approximated by an expression ![]() . Then the system of
equations (4) has the form
. Then the system of
equations (4) has the form
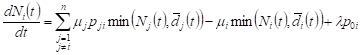 , , | (5) |
This is a system of regular linear differential equations with discrete right sides, which can be solved by dividing the phase spaces into a number of areas and finding solutions in each of them.
From (1), (2) it follows
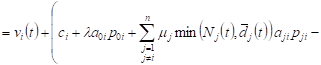
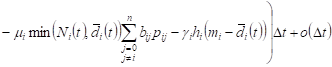 . . |
When ![]() , we
have heterogeneous first order linear equations
, we
have heterogeneous first order linear equations
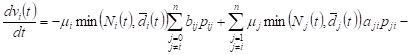
| (6) |
By
setting up the initial conditions ![]() ,
, ![]() , you can find the expected volume of network systems.
, you can find the expected volume of network systems.
If the network is functioning in such a way
that on average there are no queues in it, ie. ![]() ,
, ![]() , the formulas (5) (6) will have the form:
, the formulas (5) (6) will have the form:
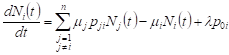 , , | (7) |
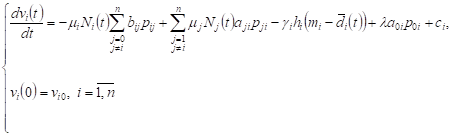 | (8) |
3. Expected volumes of requests in central network system
Let’s consider a closed network with a
central QS. Let peripheral networks
do not have queues on average, ie ![]() ,
, ![]() , and
the central system operates in high load conditions, ie
, and
the central system operates in high load conditions, ie ![]() . The system (5) in this case can be
rewritten as
. The system (5) in this case can be
rewritten as
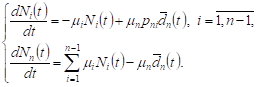 | (9) |
The general solution of the system (9) having
(3) at the initial conditions, ![]() ,
,
![]() , is equal
, is equal
where ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
number of requests
in the network. For those
-
number of requests
in the network. For those ![]() ,
, ![]() , the system (8) for the expected volume
of requests in network systems takes the form
, the system (8) for the expected volume
of requests in network systems takes the form
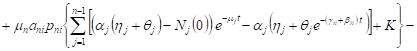
|
By integrating these systems with initial
conditions, ![]() ,
, ![]() ,
we have
,
we have
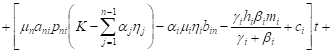
| (10) |
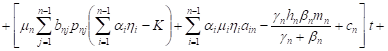
| (11) |
4. Conclusions
The article received approximate expressions for finding expected revenues in HM-network systems. These systems can be used when finding the expected memory space in information systems. Further research in this direction may be related to the analysis of arbitrary (non-Markov) random volume registrations and Markov chains applications with other peculiarities, such as limited queue time and faulty service systems.
References
[1] Tikhonenko, O. (2006). Metody personalistyczne analizy systemów informacyjnych. Akademicka Oficyna Wydawnicza EXIT.
[2] Matalytski, M., Tikhonenko, O., & Koluzaeva, E. (2011). Systems and queueing networks: analysis and application [In Russian: Sistemy i seti massovogo obsluzhivanija: analiz i primenenija]. GrSU.
[3] Bufferbloat [Electronic resource]: Wikipedia: http://en.wikipedia.org/wiki/Bufferbloat.
[4] Matalytski, M., & Statkevich, S. (2014). Stochastic network with bounded waiting time of claims and unrealiable service. [In Russian: Stohasticheskie seti s ogranichennym vremenem ozhidanija zajavok i nenadjozhnym obsluzhivaniem]. GrSU.
[5] Matalytski, M. (2015). Analysis and forecasting of expected incomes in Markov network with bounded waiting time for the claims. Automation and Remote Control, 76(6), 1005-1017.
[6] Matalytski, M., & Naumenko V. (2015). Zastosowanie HM-sieci kolejkowych dla wyznaczenia objętości pamięci systemów informacyjnych. Studia Informatica, 35(3), 63-69.
[7] Matalytski, M., & Zajac, P. (2016). Finding of expected volumes of request in systems of the queueing network with limited amount of spaces of expectations. Studia Informatica, 36(1), 89-104.
[8] Matalytski, M., & Zajac, P. (2017). Expected volumes of requests in systems of the queueing network with a limited number of waiting places. Scientific Issues Jan Długosz University in Częstochowa Mathematics XXII, 141-160.
[9] Matalytski M., & Zajac, P. (2017). Application of HM-networks with impatient claims in finding the memory capacity in the information systems. Journal of Applied Mathematics and Computational Mechanics, 16(3), 47-59.


