Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Sobamowo_2018,
   doi = {10.17512/jamcm.2018.2.06},
   url = {https://doi.org/10.17512/jamcm.2018.2.06},
   year = 2018,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {17},
   number = {2},
   pages = {65--76},
   author = {Gbeminiyi Sobamowo and  Olurotimi Adeleye},
   title = {Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2018.2.06
UR  - https://doi.org/10.17512/jamcm.2018.2.06
TI  - Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Sobamowo, Gbeminiyi
AU  - Adeleye, Olurotimi
PY  - 2018
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 65
EP  - 76
IS  - 2
VL  - 17
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Sobamowo, G., & Adeleye, O. (2018). Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease. Journal of Applied Mathematics and Computational Mechanics, 17(2), 65-76. doi:10.17512/jamcm.2018.2.06

Sobamowo, G. & Adeleye, O., 2018. Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease. Journal of Applied Mathematics and Computational Mechanics, 17(2), pp.65-76. Available at: https://doi.org/10.17512/jamcm.2018.2.06

[1]G. Sobamowo and O. Adeleye, "Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 2, pp. 65-76, 2018.

Sobamowo, Gbeminiyi, and Olurotimi Adeleye. "Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease." Journal of Applied Mathematics and Computational Mechanics 17.2 (2018): 65-76. CrossRef. Web.

1. Sobamowo G, Adeleye O. Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(2):65-76. Available from: https://doi.org/10.17512/jamcm.2018.2.06

Sobamowo, Gbeminiyi, and Olurotimi Adeleye. "Application of Daftardar-Gejiji and Jafari Method to kinetic analysis of thermal inactivation of Jack Bean Urease." Journal of Applied Mathematics and Computational Mechanics 17, no. 2 (2018): 65-76. doi:10.17512/jamcm.2018.2.06

APPLICATION OF DAFTARDAR-GEJIJI AND JAFARI METHOD TO KINETIC ANALYSIS OF THERMAL INACTIVATION OF JACK BEAN UREASE

Gbeminiyi Sobamowo ¹, Olurotimi Adeleye ²

¹ Department of Mechanical Engineering, University of Lagos, Akoka, Lagos, Nigeria
² Department of System Engineering, University of Lagos, Akoka, Lagos, Nigeria
mikegbeminiyi@gmail.com, rotimiadeleye1711@gmail.com

Received: 9 December 2017; Accepted: 26 June 2018

Abstract. Jack bean urease has been used as a good catalyst for hydrolysis of urea in various applications such as biotechnology and biomedical engineering. The wide range of applications require proper understanding of the thermal inactivation of the enzyme. Consequently, the theoretical analysis of the enzyme kinetic of the thermal inactivation is required. In this paper, a new iterative method proposed by Daftardar-Gejiji and the Jafari method is applied to analyse the kinetic of thermal inactivation of jack bean urease (EC3.5.1.5). The kinetics of the urease consist of three-reaction steps and included the Arrhenius equation for temperature-dependent rate constants as well as the temperature change in the initial heating period. The approximate analytical solutions are verified with results of numerical method using Runge-Kutta with the shooting method, and good agreements are established between the results of the methods. From the analytical investigation, it is established that the molar concentration of the native enzyme decreases as the time increases while the molar concentration of the denatured enzyme increases as the time increases. The time taken to reach the maximum value of the molar concentration of the native enzyme is the same as the time taken to reach the minimum value of the molar concentration of the denature enzyme. It is hoped that the information given in this theoretical investigation will assist in the kinetic analysis of thermal inactivation of the experimental results over handling rate constants and molar concentrations.

MSC 2010: 35A15

Keywords: kinetics, thermal activation, jack bean urease, enzyme, biotechnology, Daftardar-Gejiji and Jafari method

1. Introduction

Functionally, urease (urea amino hydrolase E.C.3.5.1.5) are parts of the superfamily of amidohydrolases and phosphotriesterases. It is a highly efficient catalyst that catalyses the hydrolysis of urea into carbon dioxide and ammonia. It catalyses at a rate approximately 10¹⁴ times faster than the rate of the non-catalysed reaction [1]. The hydrolysis of urea is catalysed by urease to produce ammonia and carbamate, and the carbamate produced is subsequently degraded by spontaneous hydrolysis to produce another ammonia and carbonic acid. Urease activity tends to increase the pH of its environment as it produces ammonia.

Jack bean urease, which is the most widely used plant urease, is a nickel containing oligomeric enzyme exhibiting a high degree of specifity to urea [2]. The importance and applications of the urease as a good catalyst for hydrolysis of urea have attracted several research interests [3-15] especially in biotechnology and biomedical engineering. Also, the thermostability of jack bean urease has often been a subject of investigations [14]. However, there are few studies where the temporal loss of enzyme activity and the kinetic analysis of heat induced decay of enzyme activity were presented. Moreover, none of these studies involved consistent evaluations of kinetics of the urease inactivation. Most of the past studies described the complex mechanisms of thermal deactivation of enzymes as a “one step - two states” process where the native (active) form is transformed in the denaturated (inactive) form by a first order unimolecular irreversible reaction [14]. This unifying simplification is of interest for researchers focusing attention on the phenomenological process rather than the mechanistic description of the kinetics of heat induced enzyme deactivation. However, the multi-temperature evaluations revealed that an adequate kinetic model has to incorporate at least three reaction steps [14]. Although, the three-step mechanism model of inactivation of the enzyme has been developed by Illeova et al. [16], there is no provision of either exact or approximate analytical solutions (except by Ananthi et al. [16]) for the predictions of model concentrations of the native enzyme, denature enzyme and temperature for thermal inactivation of urease. Ananthi et al. [16] applied the homotopy analysis method to develop approximate analytical solutions for the analysis of kinetic and thermal inactivation of the enzyme. However, the use of HAM in the analysis of linear and nonlinear equations requires the determination of an auxiliary parameter that will increase the computational cost and time. Also, the lack of rigorous theories or proper guidance for choosing initial approximation, auxiliary linear operators, auxiliary functions, auxiliary parameters, and the requirements of conformity of the solution to the rule of coefficient ergodicity, limits the applications of HAM. Moreover, such a method requires a high level of skill in mathematical analysis. Consequently, a direct and relatively simple method is needed to establish an analytical solution for the kinetic of thermal inactivation of the urease.

The new iterative method by the Daftardar-Jafari method (DJM), developed in 2006 has proven to be highly efficient in solving linear and nonlinear problems of integer and fractional order [17-24]. DJM is an improvement on the Adomian decomposition method. However, unlike the Adomian decomposition method, where the calculation of the tedious Adomian polynomials is needed to deal with nonlinear terms, DJM handles linear and nonlinear terms in a simple and straightforward manner without any additional requirements. The method converges to the exact solution if it exists through successive approximations [17-24]. It comes with the associated error control procedures. DJM solves nonlinear differential equations of integral and fractional order without perturbation, linearization, discretization or a round-off error. It reduces the complexity of expansion of derivatives and the computational difficulties of the other traditional methods. It is capable of greatly reducing the size of computational work while still accurately providing the series solution with a fast convergence rate [17-24]. Therefore, in this work, a new iterative method proposed by Daftardar-Gejiji and Jarari (DJ method) is applied to analyze the kinetic of thermal inactivation of jack bean urease (EC3.5.1.5). The developed analytical solutions are used to study the effects of the parameters of the models on the molar concentration of the native and denatured enzyme.

2. Model formulation

The three - step mechanism of inactivation with a dissociation reaction of the native form of the enzyme, N, into a denatured form, D, and with two parallel association reactions of the native and denatured forms into irreversible denatured enzymes forms and , respectively.

(1)

where , , and represent the rate constants of individual reactions. The material balances equations for , and temperature are given as follows:

(2a)

(2b)

(2c)

Initial conditions are

,,

(3)

The kinetic model was formed by the set of nonlinear ordinary differential equations (Eqs. (2a)-(2c)). The core of the kinetic model was formed by the material balances of the forms N and D (Eqs. (2a) and (2b)). The third equation of the model was the enthalpy balance (Eq. (2c)) describing the initial heating period

Let c_N , c_D , , , and by X, Y, , , and , respectively, Eqs. 2a and 2b become

(4a)

(4b)

, (5)

while the exact solution of Eq. (2c) is given as

(6)

3. Method of solution: Daftardar-Gejiji and Jarari Metod (DJ method)

It is very difficult to develop a closed-form solution for the above nonlinear Eqs. (4a) and (4b). Therefore, a new iterative method proposed by Daftardar-Gejiji and Jarari (DJ method) is applied to analyze the nonlinear equation. The basic definitions and procedure of the method are given as follows:

Consider the following general functional equation

(7)

where N is a nonlinear operator from a Banach space and f is a known function . The solution u in Eq. (7) have a series solution of the form

(8)

The nonlinear operator N can be decomposed as

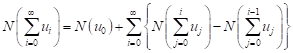(9)

From equations (8) and (9), equation (7) is equivalent to

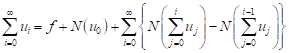(10)

We define the recurrence relation

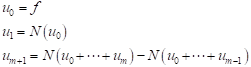(11)

then

(12)

and

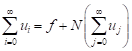(13)

The k - term approximate solution of Eq. (7) is given by

(14)

Integrating the above Eqs. (4a) and (4b)

(15a)

(15b)

Appling the initial condition, , we have,

(16a)

(16b)

From Eqs. (16a) and (16b)

,

(17a)

and

,

(17b)

Following DJM

(18)

After the integration, we have

(19)

Also,

(20)

Which gives

(21)

and

(22)

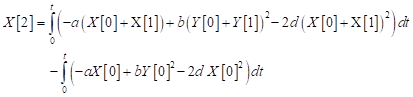(23)

The solution of Eq. (23) is given as

(24)

Also, for

(25)

one gets

(26)

Furthermore, according to DJM

(27)

which gives

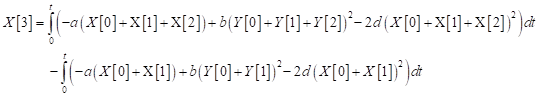(28)

Therefore,

(29a)

(29b)

Equations (29a) and (29b) form the approximate analytical solutions of concentrations of the native and denatured enzyme. The analytical solutions are simulated and the results are shown below.

4. Results and discussion

Tables 1 and 2 show the comparison between the results of DJM and NM. The obtained results of using DJM as compared with the numerical procedure using the Runge-Kutta method coupled with the shooting method are in good agreements. The high accuracy of DJM gives high confidence about validity of the method in providing solutions to the problem.

Table 1

Comparison of results for X(t)

Table 2

Comparison of results for Y(t)

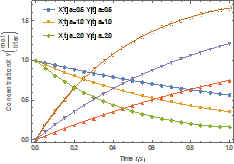
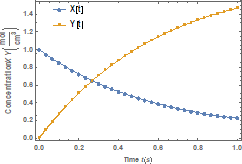
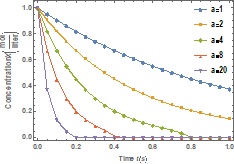
Fig. 1. Molar concentrations of native and denatured enzyme when	Fig. 2. Effects of dissociation native rate constant () on molar concentration of denatured enzyme when
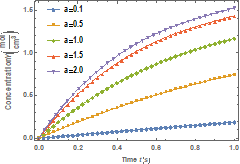
Fig. 3. Effects of dissociation native rate constant () on molar concentration of native enzyme when	Fig. 4. Effects of dissociation native rate constant () on molar concentration of native enzyme when
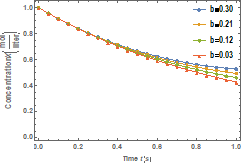
Fig. 5. Effects of dissociation native rate constant () on molar concentration of denatured enzyme when	Fig. 6. Effects of dissociation native rate constant () on molar concentration of native enzyme when

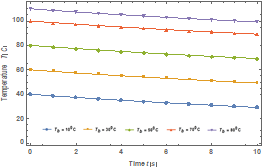
Fig. 7. Temperature variation with time of the enzyme when

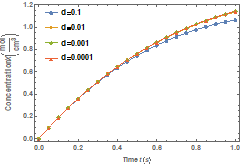
Figure 1 shows variation of the molar concentration of native and denatured enzyme with time when . As depicted in the figure, the molar concentration of the native enzyme decreases as the time increases while the molar concentration of the denatured enzyme increases as the time increases. The time taken to reach the maximum value of the molar concentration of the native enzyme is the same as the time taken to reach the minimum value of the molar concentration of the denature enzyme. The steady values of molar concentrations of the native and denatured enzyme depend upon the rate constants.

Figure 2 shows the effects of the dissociation native rate constant () on the molar concentration of the denatured enzyme while Figure 3 depicts the effects of the dissociation native rate constant () on molar concentration of the native enzyme when .

From these figures, it is found that the value of molar concentration of the denatured enzyme initially increases and reaches the steady state value when 𝑡 ≥ 5. Also, the molar concentration of the denatured enzyme increases when 𝑘 increases and the molar concentration becomes zero when 𝑘₊₁ £ 0.01 s⁻¹. Figure 4 presents the effects of the dissociation native rate constant () on molar concentration of the native enzyme when while Figure 5 shows the effects of dissociation native rate constant () on molar concentration of the denatured enzyme when . Effects of the dissociation native rate constant () on molar concentration of native enzyme whenare shown in Figure 6.

Figure 7 shows the temperature history of the enzyme when . Also, effects of bath temperature on the temperature history are depicted in the figure. The temperature of the enzyme decreases linearly with time. It could be seen that as the bath temperature, 𝑇_𝐵 increases, the temperature of the enzyme increases.

4. Conclusions

In this work, approximate analytical solutions for the analysis of the kinetic model of thermal inactivation of the jack bean urease (E.C.3.5.1.5) have been developed using a new iterative method proposed by Daftardar-Gejiji and Jafari (DJ method). The analytical solutions are verified with a numerical solution using the Runge-Kutta method coupled with the shooting method and good agreements were established. It is hoped that the information given in this theoretical investigation will assist in the kinetic analysis of the experimental results over handling rate constants and molar concentrations.

Nomenclature

c_N - molar concentration of the native enzyme form [mole/cm]

c_D - molar concentration of the denaturedenzyme form [mole/cm]

k_–1, k₊₁, k₂, k₃ - rate constants of individual reaction [s^–1]

k’_–1, k’₂, k’₃ - modified rate constants [s⁻¹]

𝐾 - coefficient in the enthalpy balance [s]

𝑇_B - bath temperature [K]

𝑇 - temperature [K]

𝑡 - time

References

[1] Quin, Y., & Cabral, J.M. (2002). Properties and applications of urease. Biocatal. Biotransform., 20, 227-236, 2002.

[2] Dixon, N.E., Gazzola, C., Blakeley, R.L., & Zerner, B. (1975). Jack bean urease (E.C.3.5.1.5). A metalloenzyme. A simple biological role for nickel. J. Am. Chem. Soc., 97, 4131-4133.

[3] Winquist, F., Lundstroem, L., & Danielsson, B. (1988). Trace level analysis for mercury using urease in combination with an ammonia gas sensitive semiconductor structure. Anal. Lett. B, 21, 1801-1816.

[4] Miyagawa, K., Sumida, M., Nakao, M., Harada, M., Yamamoto, H., Kusumi, T., Yoshizawa, K., Amachi, T., & Nakayama, T. (1999). Purification, characterization and application of an acid urease from Arthrobacter mobilis. J. Biotechnol., 68, 227-236.

[5] Sansubrino, A., & Mascini, M. (1994). Development of an optical fibre sensor for ammonia, urea, urease and IgG. Biosens. Bioelectron., 9, 207-216.

[6] Godjevargova, T., & Dimov, A. (1997). Immobilization of urease onto membranes of modified acrylonitrile copolymer. J. Membr. Sci., 135, 93-98.

[7] Rejikumar, S., & Devi, S. (1998). Preparation and characterization of urease bound on crosslinked poly(vinyl alcohol). J. Mol. Catal. B, 4, 61-66.

[8] Chen, J.P., & Chiu, S.H. (2000). A poly(n-sopropylacrylamide-co-Nacroloxysuccinimide-co-2-hydroxyetyl methacrylate) composite hydrogel membrane for urease immobilization to enhance urea hydrolysis rate by temperature swing. Enzyme Microb. Technol., 26, 359-367.

[9] Lencki, W.R., Arul, J., & Neufeld R.J. (1992). Effect of subunit dissociation, denaturation, aggregation, coagulation, and decomposition on enzyme inactivation kinetics. II. Biphasic and grace period behavior. Biotechnol. Bioeng., 40, 1427-1434.

[10] Gianfreda, I., Marucci, G., Grizzuti, N., & Greco, G. (1985). Series mechanism of enzyme deactivation. Characterization of intermediate forms. Biotechnology and Bioengineering, 27, 877- 882.

[11] Garcia, D., Ortega, F., & Marty J-L. (1988). Kinetics of thermal inactivation of horseradish peroxidase:stabilizing effect of methoxypoly(ethylene glycol). Biotechnology and Applied Biochemistry, 27, 49-54.

[12] Fischer, J., Ulbrich, R., Zeimann, R., Flaten, S., Walna, P., Schleif, M., Pluschke, V., & Schellen- berg, A. (1980). Thermal inactivation of immobilized enzymes. A kinetic study. Journal of Solid-phase Biochemistry, 5, 79-83.

[13] Ling, A.C., & Lund, D.B. (1978). Determining kinetic parameters for thermal inactivation of heat-resistant and heat-labile isoenzymes from thermal destruction curves. Journal of Food Science, 43, 1307-1310.

[14] Illeova, V., Polakovic, M., Stefuca, V., Acai, P., & Juma, M. (2003). Experimental modelling of thermal inactivation of urease. Journal of Biotechnology, 105(3), 235-243.

[15] Arroyo, M., Sanchez-Montero, J.M., & Sinisterra, J.V. (1999). Thermal stabilization of immobilized lipase B from Candida antartica on different supports: effect of water activity on enzyme activity in organic media. Enzyme and Microbial Technology, 24, 3-12.

[16] Ananthi, S.P., Manimozhi, P., Praveen, T., Eswari, A., & Rajendran, L. (2013). Mathematical Modeling and Analysis of the Kinetics of Thermal Inactivation of Enzyme. International Journal of Engineering Mathematics, Article ID 132827, 8 pages.

[17] Zhou, J.K. (1986). Differential Transformation and Its Applications for Electrical Circuits. Huazhong University Press, Wuhan, China (in Chinese).

[18] Daftardar-Gejji, V., & Hossein, J. (2006). An iterative method for solving nonlinear functional equations. J. Math Appl., 316, 753-763.

[19] Bhalekar, S., & Daftardar-Gejji, V. (2008). New iterative method: application topartial differntial equations. Appl. Math. Comput., 203, 778-783.

[20] Daftardar-Gejji, V., & Bhalekar, S. (2010). Solving fractional boundary value problems with Dirichlet boundary conditions using a new iterative method. Comput. Math. Appl., 59, 1801-1809.

[21] Daftardar-Gejji, V., & Bhalekar, S. (2008). An iterative method for solving fractional differential equations. Proc. Appl. Math. Mech., 7:2050017-18.

[22] Bhalekar, S., & Daftardar-Gejji, V. (2010). Solving evolution equations using a new iterativemethod. Numer Methods Partial Differ Equat., 26, 906-916.

[23] Jafari, H., Seifi, S., Alipoor, A., & Zabihi, M. (2009). An iterative method for solving linear andnonlinear fractional diffusion-wave equation. Int. e-J Numer Anal. Relat. Topics, 3, 20-32.

[24] Yaseen, M., & Samraiz, M. (2012). A modified new iterative method for solving linear andnonlinear Klein-Gordon Equations. Appl. Math. Sci., 6, 2979-2987.