Numerical analysis of strains and stresses in the hot cogging process
Marcin Kukuryk
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Kukuryk_2018,
doi = {10.17512/jamcm.2018.3.04},
url = {https://doi.org/10.17512/jamcm.2018.3.04},
year = 2018,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {17},
number = {3},
pages = {45--52},
author = {Marcin Kukuryk},
title = {Numerical analysis of strains and stresses in the hot cogging process},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2018.3.04 UR - https://doi.org/10.17512/jamcm.2018.3.04 TI - Numerical analysis of strains and stresses in the hot cogging process T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Kukuryk, Marcin PY - 2018 PB - The Publishing Office of Czestochowa University of Technology SP - 45 EP - 52 IS - 3 VL - 17 SN - 2299-9965 SN - 2353-0588 ER -
Kukuryk, M. (2018). Numerical analysis of strains and stresses in the hot cogging process. Journal of Applied Mathematics and Computational Mechanics, 17(3), 45-52. doi:10.17512/jamcm.2018.3.04
Kukuryk, M., 2018. Numerical analysis of strains and stresses in the hot cogging process. Journal of Applied Mathematics and Computational Mechanics, 17(3), pp.45-52. Available at: https://doi.org/10.17512/jamcm.2018.3.04
[1]M. Kukuryk, "Numerical analysis of strains and stresses in the hot cogging process," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 3, pp. 45-52, 2018.
Kukuryk, Marcin. "Numerical analysis of strains and stresses in the hot cogging process." Journal of Applied Mathematics and Computational Mechanics 17.3 (2018): 45-52. CrossRef. Web.
1. Kukuryk M. Numerical analysis of strains and stresses in the hot cogging process. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(3):45-52. Available from: https://doi.org/10.17512/jamcm.2018.3.04
Kukuryk, Marcin. "Numerical analysis of strains and stresses in the hot cogging process." Journal of Applied Mathematics and Computational Mechanics 17, no. 3 (2018): 45-52. doi:10.17512/jamcm.2018.3.04
NUMERICAL ANALYSIS OF STRAINS AND STRESSES IN THE HOT COGGING PROCESS
Marcin Kukuryk
Institute of Mechanical Technology,
Czestochowa University of Technology
Częstochowa, Poland
kukurykm@itm.pcz.pl
Received: 22 August 2018;
Accepted: 15 October 2018
Abstract. In this paper, the analysis of the three-dimensional strain state for the hot cogging process of a steel tool with the application of the finite element method is presented. The results of work connected with the simulation of metal flow scheme, and fields of stress, strain and temperature in the material deformation process in the hot forging condi- tions are presented. The distribution of the effective strain, the effective stress, mean stresses and temperature on the surface of forging cross sections are determined. The numerical analysis was performed with the application of the programme DEFORM-3D. The theoretical results are subjected to experimental verification.
MSC 2010: 97N40, 80M10, 74A10
Keywords: numerical analysis, FEM, strains, stresses, temperature, hot cogging
1. Introduction
The objective of contemporary forging technologies is to obtain forgings having very high quality, i.e. such that have a required shape and dimensional tolerance, and also obtain properties which are optimal from the point of view of product functional characteristics [1, 2]. The complexity of physical-mechanical phenomena accompanying the plastic strain process at elevated temperatures makes it necessary to apply numerical modelling, which provides a large quantity of information for the purpose of process optimizing, which would be impossible to obtain in a laboratory [3, 4]. An additional setback is the diversity and non-stationary character of the kinematic conditions of deformation, and also the complexity of the stress state and strain state in the course of forging. What is particularly important is the state of strain and stress in the axis of a forged material determined, first and foremost, by the shape of a tool, and also values of the applied technological parameters [5, 6]. The knowledge of the strain and stress state in the course of the forging process makes it possible to determine the areas of the greatest plastic deformations and the places of possible material fractures [7, 8]. Determining the temperature distribution inside the strain zone in the course of the forging process of alloy tool steels is important due to the influence of temperature on the properties of deformed metal [9, 10]. Therefore, by means of controlling changes in the thermal-mechani- cal state of deformation in the course of the forging process, it is possible to exert significant influence on the mechanical and functional characteristics of products [11, 12]. Based on DEFORM 3D-software, the thermal-mechanical coupled model of the cogging process was established to investigate the effect of cogging parameters and tool shape. Based on the rigid-plastic FEM model, the evolution of mean stress, effective stress, effective strain and the deformation temperature distribution in the cogging process was presented for the selected trapezoid anvils, and also the skewed. The influence of the tool shape on the uniformity of the stress and strain distribution and resizing during cogging process has not been fully studied in the previous known publications.
2. Numerical model
This study a three-dimensional rigid-plastic finite element method was used in the simulation of metal flow and heat transfer during the process of forging of the 55NiCrMoV7 steel. The basis equations of the rigid - plastic FEM are as follows:
The equilibrium equation:
 | (1) |
Compatibility equation and the incompressibility condition:
 ,  | (2) |
The constitutive relationship:
 | (3) |
where:
 ,  ,  ,  ,  | (4) |
Boundary conditions:
 on SF ,  on SV | (5) |
where 
, 
, 
are the effective strain, effective stress and
effective strain rate,
respectively, 
and 
are the components of the
stress tensor and the compo-
nents of strain rate tensor, respectively, Fj is the force on the
boundary surface
of SF , and Vi is
the deformation velocity on the boundary surface of SV .
The weak form of the rigid - plastic finite element method can be determined by applying the variational method to Eqs. (1)-(5), i.e.
 | (6) |
where 
is the volume strain rate, K the penalty constant (here
is set to be 106),
V and S are the volume and the surface area of a deformed
workpiece, respectively, 
is the
virtual velocity, 
is the virtual effective strain rate, 
is the virtual volumetric strain rate.
The analysis of heat transfer can be obtained by solving the following energy balance equation:
 | (7) |
where 
is the heat generation rate, k(T) is the
thermal conductivity, T is the temperature, ρ(T) is specific density, 
is specific heat, and T is temperature. The
first term represents the heat transfer rate and the third term is the heat
generation rate. Due to plastic deformation, the rate of the heat generation in
the deformed material is given as:
 | (8) |
where β is the heat generation efficiency and represents the fraction of mechanical energy converted into heat (here assumed to be 0.90).
The energy equation, Eq. (7), can be rewritten using the weighted residual method as:
 | (9) |
where 
is
the heat flux normal to the boundary surface. The temperature distribu-
tion of the workpieces can be obtained by solving the
above energy balance equation. Equations (6) and (9) can be converted into a
system of algebraic equations. The Newton-Raphson iteration method is applied
to obtain the solution of the equations. The solutions of mechanical and
thermal problems are coupled in a staggered manner.
The frictional boundary condition is defined as:
 | (10) |
where 
is the friction
factor, τk is the local flow stress in shear, vs is the
velocity vector of the workpiece relative to the anvil, t is the unit
vector in the direction
of vs and u0 is a constant of magnitude
10–5.
3. Numerical simulation
For the 3D modeling of metal plastic flow in the course of cogging, the professional computer program DEFORM-3D was applied; this program made it possible to simulate the researched forging process in thermal and mechanical terms. In numerical calculations and the experimental study, the following charge was assumed: diameter - 80 mm, length - 200 mm, material 55NiCrMoV7 steel. The simulation of hot cogging has been performed under the same condition of the experiment. The forging was conducted on a hydraulic press with a force 2.5 MN, in two consecutive passes, with the turning angle of 90° (the reduction ratio εh = 0.70). The speed of the hydraulic press amounted to 20 mm/s. The initial temperature of the deformed material was 1100°C, and that of the anvils to 300°C. In the simulation, the friction factor between forging and the anvil was assumed as 0.7, the billet surface emissivity was 0.7, and the Poisson’s ratio was 0.3. The gravitational effects were neglected. The simulation was carried out under non-isothermal conditions. In every pass, forging in the trapezoid anvils (Fig. 1a) was conducted in two stages: the first stage was that of deformation on trapezoid anvils and the second of removing the formed concavity on flat-surface anvils. Forging on skew anvils (Fig. 1b) was conducted with the application of the traditional method taking into account interoperational turning.
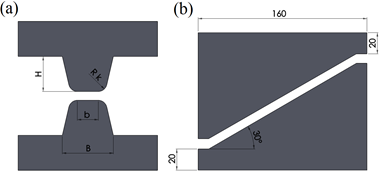
Fig. 1. (a) The trapezoid anvils: rk = 10 mm, b = 40 mm, H = 40 mm, B = 80 mm, (b) The skew anvils (α = 30°)
The results of the numerical calculations of
forging on trapezoid anvils after
the second pass are presented in Figure 2. The area with the maximum values of
the effective strain was that of the central part of the deformation valley,
and
it amounted to 
= 0.90¸1.00
(Fig. 2a). In the corners, and on the contact surfaces of the forging with the tool, somewhat smaller values of the
distribution of the
effective strain were obtained,
namely = 0.60¸0.80. The even distribution of
the effective strain was accompanied by the even
distribution of the effective stresses on
the surface of the cross-section of a forging, namely σi = 120¸140 MPa (Fig. 2b). Virtually on the entire surface of the
cross-section, favourable compressive stresses were observed; the only
exception was that on small areas in the corners of forging it was possible to
observe small values of the tensile stress (Fig. 2c). Large values of the
effective strain on the best part of the surface of the cross-section shaped
on trapezoid anvils was conducive to generating significant values of plastic
deformation work converted into thermal energy, which was conducive to thermal
stability in the course of deformation in the internal zones of forging (Fig. 2d).
It was only on the contact surfaces between hot metal and cooler anvils that
a decrease in temperature by DT = 90¸130°C was
observed (Fig. 2d).
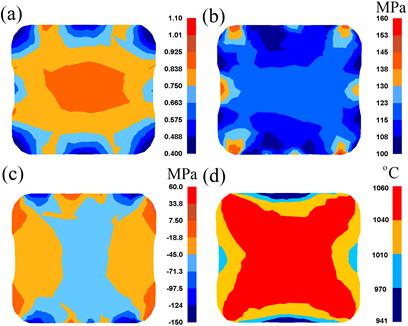
Fig. 2. Distribution of effective strain (a), effective stress (b), mean stress (c) and temperature (d) in the middle cross-section of the specimens after the cogging process on trapezoid anvils with a reduction ratio εh = 0.70
The results of numerical calculations on skew
anvils after the second pass
are presented in Figure 3. The largest deformation occurred in the central part
of
a forging and amounted to = 0.60¸0.80
(Fig. 3a). In the corners, and on the con-
tact surfaces of the forging with the application of a
tool, much smaller values of the
distribution of the effective strain, namely = 0.40¸0.50,
were obtained. Such a distribution of the effective
strain on the surface of the cross-section of a forging was accompanied by a
distribution of the effective stresses similar to that obtained on trapezoid
anvils, namely σi = 117¸149 MPa (Fig. 3b). The analysis of the
diagrams shows significantly greater diversity of the effective strain, and
also
displays mean stresses, in particular in the areas of the zone of deformation
in comparison with those obtained on trapezoid anvils. However, the mean
stresses σm in
the central part of the deformation valley were compressive, which has a
significant influence on the internal quality of the forgings. It is only in
the lateral zones of the forging that it is possible to expect the presence of
small tensile stresses
(Fig. 3c). It was observed, as during shaping in trapezoid anvils, thermal
stability in the central parts of the
forging (Fig. 3d). It was only on the contact surfaces between hot metal
and cooler anvils that decrease in temperature by DT = 90¸130°C was observed.
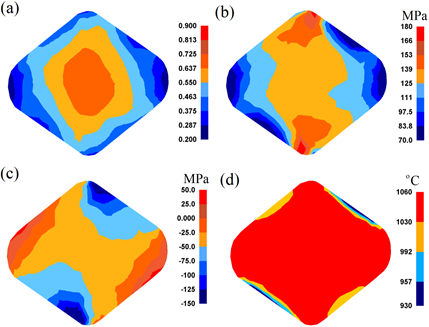
Fig. 3. Distribution of effective strain (a), effective stress (b), mean stress (c) and temperature (d) in the middle cross-section of the specimens after the cogging process on the skew anvils with a reduction ratio εh = 0.70
The experiment was conducted to validate the proposed model by comparing the effective strain and the deformation temperature between the experimental measurements and simulation results. The results are presented in Figure 4. The state of deformation was determined with the application of the coordination grid method. The initial temperature of the deformed material was 1100°C. The detailed description of that method is presented in the work [13]. Temperature was measured at selected points on the surface of the deformed forging with the application of a thermal thermovision-camera (the emissivity was 0.7). The conducted comparative analysis of the effective strain, and also the temperature obtained in numerical calculations, and obtained by means of experiments, showed their relatively good compatibility.
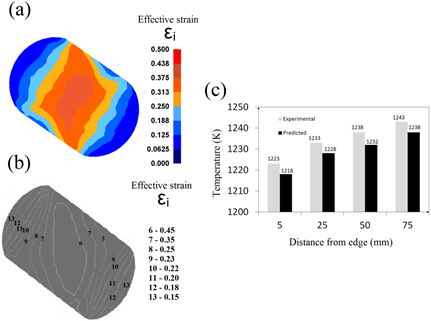
Fig. 4. Comparison between the simulated (a) and experimental (b) effective strain distribution (reduction ratio ɛh = 0.35) and variation of the temperature at selected points of the deformation valley ((c), ɛh = 0.70) after the cogging process in the skew anvils
4. Conclusions
The conducted numerical research, confirmed by means of experiments, made it possible to determine the local conditions describing the state of strain and stress, and also the distribution of temperature, in the course of forging a tool steel, on trapezoid and skew anvils. Both kinds of forging tools deserve the name of high efficiency in terms the distribution of the effective strain, stresses, absence of tensile stresses in the axial zones of a forging, and also high thermal stability of the internal zones of the deformed material. At the initial stages of forging, it is proposed that more effective trapezoid anvils be applied, whereas further, and also finally, forging may be conducted on versatile skew anvils. The conducted research confirmed that, by means of choosing an appropriate shape and geometry of the working surface of anvils, and also relevant technological parameters, it is possible to significantly influence: the location of the maximum values of the effective strain and stresses, the value of the unevenness of the distribution of the effective strain, and also reducing of tensile stresses in the deformation valley, which makes it possible to objectively control the internal quality of a forging and the level of product properties.
References
[1] Du, F., Wang, M., & Li, X. (2007). Research on deformation and microstructure evolution during forging of large-scale parts. Journal of Materials Processing Technology, 187-188, 591-594. DOI: 10.1016/j.jmatprotec.2006.11.038.
[2] Choi, S., Chun, M., Tyne, C. V., & Moon, Y. (2006). Optimization of open die forging of round shapes using FEM analysis. Journal of Materials Processing Technology, 172(1), 88-95. DOI: 10.1016/j.jmatprotec.2005.09.010.
[3] Wang, S., Luo, J., Hou, L., Zhang, J., & Zhuang, L. (2016). Physically based constitutive analysis and microstructural evolution of AA7050 aluminum alloy during hot compression. Materials & Design, 107, 277-289. DOI: 10.1016/j.matdes.2016.06.023.
[4] Babu, K.A., Mandal, S., Athreya, C., Shakthipriya, B., & Sarma, V.S. (2017). Hot deformation characteristics and processing map of a phosphorous modified super austenitic stainless steel. Materials & Design, 115, 262-275. DOI: 10.1016/j.matdes.2016.11.054.
[5] Duan, X., & Sheppard, T. (2002). Shape optimisation using FEA software: A V-shaped anvil as an example. Journal of Materials Processing Technology, 120(1-3), 426-431. DOI: 10.1016/ s0924-0136(01)01200-6.
[6] Jo, H., Lee, S., Ko, D., & Kim, B. (2001). A study on the optimal tool shape design in a hot forming process. Journal of Materials Processing Technology, 111(1-3), 127-131. DOI: 10.1016/ s0924-0136(01)00537-4.
[7] Gronostajski, Z., Kaszuba, M., Polak, S., Zwierzchowski, M., Niechajowicz, A., & Hawryluk, M. (2016). The failure mechanisms of hot forging dies. Materials Science and Engineering: A, 657, 147-160. DOI: 10.1016/j.msea.2016.01.030.
[8] Miao, X., Yu, Q., Zhou, C., Li, J., Wang, Y., & He, X. (2018). Experimental and numerical investigation on fracture behavior of CTS specimen under I-II mixed mode loading. European Journal of Mechanics - A/Solids, 72, 235-244. DOI: 10.1016/j.euromechsol.2018.04.019.
[9] Babu, K.A., Mandal, S., Kumar, A., Athreya, C., Boer, B.D., & Sarma, V.S. (2016). Characterization of hot deformation behavior of alloy 617 through kinetic analysis, dynamic material modeling and microstructural studies. Materials Science and Engineering: A, 664, 177-187. DOI: 10.1016/j.msea.2016.04.004.
[10] Zhu, Z., Lu, Y., Xie, Q., Li, D., & Gao, N. (2017). Mechanical properties and dynamic constitutive model of 42CrMo steel. Materials & Design, 119, 171-179. DOI: 10.1016/ j.matdes.2017.01.066.
[11] Samal, S., Rahul, M., Kottada, R.S., & Phanikumar, G. (2016). Hot deformation behaviour and processing map of Co-Cu-Fe-Ni-Ti eutectic high entropy alloy. Materials Science and Engineering: A, 664, 227-235. DOI: 10.1016/j.msea.2016.04.006.
[12] Switzner, N., Tyne, C.V., & Mataya, M. (2010). Effect of forging strain rate and deformation temperature on the mechanical properties of warm-worked 304L stainless steel. Journal of Materials Processing Technology, 210(8), 998-1007. DOI: 10.1016/j.jmatprotec.2010.01.014.
[13] Kukuryk, M. (2016). Analysis of deformation and damage evolution in the forging process of Waspaloy alloy. Rudy i Metale Nieżelazne Recykling, 61(7), 331-336. DOI: 10.15199/ 67.2016.8.1.
