Lie symmetries and conserved quantities of discrete constrained Hamilton systems
Zheng Mingliang
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Mingliang_2018,
doi = {10.17512/jamcm.2018.3.06},
url = {https://doi.org/10.17512/jamcm.2018.3.06},
year = 2018,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {17},
number = {3},
pages = {61--70},
author = {Zheng Mingliang},
title = {Lie symmetries and conserved quantities of discrete constrained Hamilton systems},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2018.3.06 UR - https://doi.org/10.17512/jamcm.2018.3.06 TI - Lie symmetries and conserved quantities of discrete constrained Hamilton systems T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Mingliang, Zheng PY - 2018 PB - The Publishing Office of Czestochowa University of Technology SP - 61 EP - 70 IS - 3 VL - 17 SN - 2299-9965 SN - 2353-0588 ER -
Mingliang, Z. (2018). Lie symmetries and conserved quantities of discrete constrained Hamilton systems. Journal of Applied Mathematics and Computational Mechanics, 17(3), 61-70. doi:10.17512/jamcm.2018.3.06
Mingliang, Z., 2018. Lie symmetries and conserved quantities of discrete constrained Hamilton systems. Journal of Applied Mathematics and Computational Mechanics, 17(3), pp.61-70. Available at: https://doi.org/10.17512/jamcm.2018.3.06
[1]Z. Mingliang, "Lie symmetries and conserved quantities of discrete constrained Hamilton systems," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 3, pp. 61-70, 2018.
Mingliang, Zheng. "Lie symmetries and conserved quantities of discrete constrained Hamilton systems." Journal of Applied Mathematics and Computational Mechanics 17.3 (2018): 61-70. CrossRef. Web.
1. Mingliang Z. Lie symmetries and conserved quantities of discrete constrained Hamilton systems. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(3):61-70. Available from: https://doi.org/10.17512/jamcm.2018.3.06
Mingliang, Zheng. "Lie symmetries and conserved quantities of discrete constrained Hamilton systems." Journal of Applied Mathematics and Computational Mechanics 17, no. 3 (2018): 61-70. doi:10.17512/jamcm.2018.3.06
LIE SYMMETRIES AND CONSERVED QUANTITIES OF DISCRETE CONSTRAINED HAMILTON SYSTEMS
Zheng Mingliang
School of Electrical and Mechanical
Engineering, Taihu University of Wuxi
Wuxi, China
zhmlwxcstu@163.com
Received: 6 August 2018;
Accepted: 23 October 2018
Abstract: In this paper, the Lie symmetry theory of discrete singular systems is studied in phase space. Firstly, the discrete canonical equations and the energy evolution equations of the constrained Hamilton systems are established based on the discrete difference variational principle. Secondly, the Lie point transformation of discrete group is applied to the difference equations and constraint restriction, and the Lie symmetry determination equations of the discrete constrained Hamilton systems are obtained; Meanwhile, the Lie symmetries of singular systems lead to the discrete Noehter type conserved quantities when the structure condition equations (discrete Noether identity) are established. Finally, an example is given to illustrate the application, the results show that the conservative constrained Hamilton systems also have the discrete energy conservation.
MSC 2010: 37K05, 37N70G65
Keywords: the discrete difference variational principle, constrained Hamilton systems, Lie symmetries, conserved quantities
1. Introduction
The systems described by the singular Lagrange function are called singular systems and expressed in Hamilton form in phase space. They are also referred to as constrained Hamilton systems [1]. Many important dynamic problems of mathematical physics and engineering technology are in accord with the model of constraint Hamilton systems, such as an electromagnetic field, light traversing phenomen, quantum electrodynamics, superstring theory etc. Symmetry theory [2] is a higher level rule in theoretical physics, engineering mathematics, modern mechanics and so on, and it is closely related to the conserved quantities, such as twins. In modern times, people seek conserved quantities through the symmetries that have: Noether symmetry [3], Lie symmetry [4] and Mei symmetry [5]. In recent years, the research on symmetries and conserved quantities of constrained Hamilton systems are paid more and more attention, and have made some progress [6-10].
The theory of symmetry and conserved quantity for discrete mechanical systems has important theoretical and practical values for various numerical algorithms and integrability of differential equations in the fields such as computer visualization, quantum field theory, mathematical physics, economics and so on. In 1970, Cadzow [11] gave the discrete variational principle and the discrete Euler-Lagrange equations, which laid a foundation for the symmetry principle to be applied in discrete systems in the future. In 1980, on the basis of the discrete variational principle, Li Zhengdao [12] considered time as a dynamic variable to be discrete and obtained the motion equations of the discrete systems and the discrete form of energy conservation law. In 2002, Guo Hanying [13] proposed a new discrete variational method: the discrete difference variational method. This variational approach treats the difference as a geometric object and has the advantage of preserving the structure in dealing with discrete Hamilton systems. Fu Jingli and Shi Shenyang [14-16] studied the Noether symmetries and conserved quantities of discrete Lagrange-Maxwell electromechanical systems, discrete nonconservative and discrete nonholonomic constraint systems. Dorodnitsyn [17] firstly used Lie group transformation in differential equations and the lattice equations at the same time, he gave a conclusion that different Lie groups can lead to different conserved quantities. Fang Jianhui and Xia Lili [18-20] studied the Mei symmetries and conserved quantities of discrete constrained mechanical systems in form space and phase space. They were also compared with Noether symmetry and Lie symmetry. Generally speaking, the research on the symmetries and conserved quantities of discrete mechanical systems mainly focuses on the form space and nonsingular systems. There has been practically nothing written in literature about the discretization and the symmetry theory of the constrained Hamilton systems. According to the research methods about symmetries and conserved quantities of nonholonomic discrete mechanical systems, in this paper, the intrinsic constraints caused by singularity are considered, the Lie symmetry of a discrete singular singular systems in phase space is given, and I derived the conditions and form of discrete Noether conserved quantities by Lie symmetries.
2. Motion equations of discrete constrained Hamilton systems
The form of mechanical systems is determined
by n generalized coordinates
![]() and the Lagrange
function of the systems is
and the Lagrange
function of the systems is ![]() , the generalized momentum is
, the generalized momentum is ![]() , for constrained Hamilton systems, since the rank of L's
Hess matrix
, for constrained Hamilton systems, since the rank of L's
Hess matrix ![]() is
is ![]() , when the Legendre transfor-
mation
, when the Legendre transfor-
mation ![]() is used to transfer the Lagrange systems
to the Hamilton systems description, there are some constraints
between the regular variables
in phase space:
is used to transfer the Lagrange systems
to the Hamilton systems description, there are some constraints
between the regular variables
in phase space:
| (1) |
The constraints also must satisfy the restrictive conditions of virtual displacement and time variation:
| (2) |
The Hamilton functional action of the system is:
| (3) |
In the discrete mechanics systems, the
variational principle is divided into two kinds: the discrete variational
method and the discrete difference variational method. The former only uses
the difference instead of the derivative and does not preserve the difference
form, the latter regards difference as a geometric object
(independent variable), generally speaking, the discrete difference variational
principle is more practical and superior in discrete Hamilton mechanics
systems. According to the discrete difference variational method, time is
discretized into
a point sequence ![]() , the regular variables
, the regular variables ![]() and
and ![]() are
replaced by a discrete difference sequence, and the difference of time
and regular variables are expressed as:
are
replaced by a discrete difference sequence, and the difference of time
and regular variables are expressed as:
| (4) |
The corresponding discrete form of the Hamilton function is:
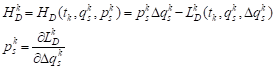 | (5) |
The formula (3) is discretized:
The ![]() is all variational operators,
is all variational operators, ![]() is isochronous variational operators,
is isochronous variational operators,
![]() is discrete derivative operators, there are the following important relationships:
is discrete derivative operators, there are the following important relationships:
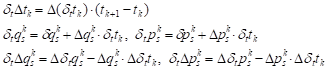 | (7) |
The ![]() is the recursion operator, the discrete Leibniz rule can be
expressed
as under the variable time step:
is the recursion operator, the discrete Leibniz rule can be
expressed
as under the variable time step:
| (8) |
According to the variational principle, the total variation of formula (6) should be as follows:
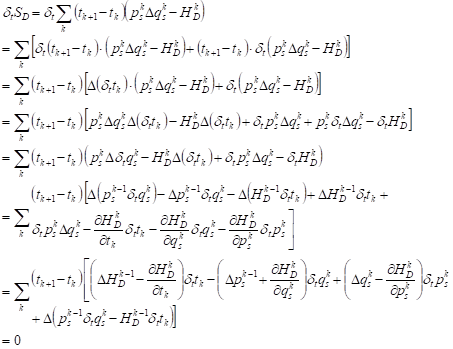 | (9) |
The discrete-time forms of internal constraints (1) and restrictive conditions (2) resulting from the singularity of the constrained Hamilton systems are:
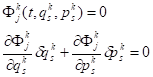 | (10) |
For
independence and independence ![]() , as long as we choose the discrete constraint multiplier
, as long as we choose the discrete constraint multiplier ![]() rationally and appropriately, it multiplies the second
equation of formula (10) and takes the sum in the interval
rationally and appropriately, it multiplies the second
equation of formula (10) and takes the sum in the interval ![]() , and then adds it to the formula (9), we can get the following
result:
, and then adds it to the formula (9), we can get the following
result:
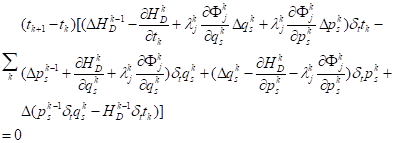 | (11) |
By using the fixed boundary conditions and
the arbitrariness of the sum ![]() interval, the regular equations of the discrete constrained Hamilton systems
are
as follows:
interval, the regular equations of the discrete constrained Hamilton systems
are
as follows:
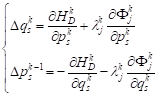 | (12) |
The energy evolution equations are as follows:
| (13) |
In this case, this article only considers the
constraint formula (1) as the second class
constraint, namely ![]()
![]() , then all
constrained multipliers
, then all
constrained multipliers ![]() can be completely determined by the
self-consistent
stability condition of
constraints [21]:
can be completely determined by the
self-consistent
stability condition of
constraints [21]: ![]() .
.
3. Lie symmetries of discrete constrained Hamilton systems
The
infinitesimal transformation of discrete time ![]() , discrete generalized coor-
dinates
, discrete generalized coor-
dinates ![]() and discrete generalized momentum
and discrete generalized momentum
![]() are:
are:
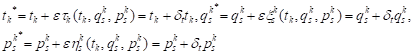 | (14) |
The vector of the infinitesimal generating element is:
| (15) |
It is important to note that the motion
difference equations (12) and (13) involve variables ![]() ,
but we regard the difference as a whole variable, the vector field (15) does
not need to expand two discrete points and three discrete points.
,
but we regard the difference as a whole variable, the vector field (15) does
not need to expand two discrete points and three discrete points.
According to the Lie symmetry definition of the mechanical systems, the invariance of the differential motion equations of the discrete constrained Hamilton systems under the infinitesimal transformation (14) is reduced to the following discrete deterministic equations:
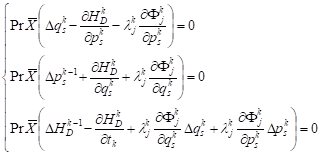 | (16) |
The discrete restriction equations with invariance of the intrinsic constraint equations (1) under the infinitesimal transformation (14) are:
| (17) |
Considering the export process of differential equations, then the infinitesimal generating element needed to meet the discrete additional restriction equations:
| (18) |
Definition
1: If the
discrete infinitesimal generating element ![]() satisfies the deterministic equations (16), the
corresponding symmetry is the Lie symmetry of the discrete-time constrained
Hamilton systems corresponding
to the discrete-time free Hamilton system.
satisfies the deterministic equations (16), the
corresponding symmetry is the Lie symmetry of the discrete-time constrained
Hamilton systems corresponding
to the discrete-time free Hamilton system.
Definition
2: If the
discrete infinitesimal generating element ![]() satisfies the deterministic equations and restriction
equations (17), the corresponding symmetry is the weak Lie symmetry of the
discrete-time constrained Hamilton systems.
satisfies the deterministic equations and restriction
equations (17), the corresponding symmetry is the weak Lie symmetry of the
discrete-time constrained Hamilton systems.
Definition
3: If the
discrete infinitesimal generating element ![]() satisfies the deterministic
equations (16), restriction
equations (17) and additional restriction equations (18), the corresponding
symmetry is the strong Lie symmetry of the
discrete-time constrained Hamilton systems.
satisfies the deterministic
equations (16), restriction
equations (17) and additional restriction equations (18), the corresponding
symmetry is the strong Lie symmetry of the
discrete-time constrained Hamilton systems.
4. Conserved quantities of discrete constrained Hamilton systems
For the constrained mechanical systems, the Lie symmetry of the system can lead to the conservation of the Noether type under certain conditions. The following theorem gives the conditions and forms about the Lie symmetries of the discrete constrained Hamilton systems leading to discrete Noether conserved quantities.
Theorem 1: According to differential
discrete variational principle, if the infini-
tesimal generating element ![]() can make the deterministic equations (16) can be established, meanwhile, there are also
normal functions
can make the deterministic equations (16) can be established, meanwhile, there are also
normal functions ![]() satisfying the following structural equations:
satisfying the following structural equations:
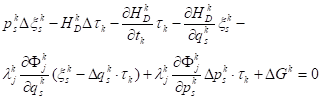 | (19) |
Then the Lie symmetry of the discrete constrained Hamilton systems leads to the discrete form of the Noether type conserved quantity:
| (20) |
At the same time, it can be seen from the above proof that the infinitesimal generating element that satisfies the structural condition equations are also the Noether quasi symmetric transformation of the discrete constrained Hamilton systems.
Theorem 2: According to differential
discrete variational principle, if the infinitesimal
generating element ![]() can make the deterministic equations
(16) and restriction
equations (17) can be
established, meanwhile, there
are also normal functions satisfying the following structural equations (19),
then the weak Lie symmetry of discrete constrained Hamilton systems leads to
the discrete conserved quantity of type (20).
can make the deterministic equations
(16) and restriction
equations (17) can be
established, meanwhile, there
are also normal functions satisfying the following structural equations (19),
then the weak Lie symmetry of discrete constrained Hamilton systems leads to
the discrete conserved quantity of type (20).
Theorem 3: According
to differential discrete variational principle, if the infinitesimal generating element ![]() can make the deterministic equations (16), restriction
equations (17) and additional restriction equations (18) can be established,
meanwhile, there are also
normal functions satisfying the following structural equation (19), then the weak Lie symmetry of discrete
constrained Hamilton systems leads to the discrete conserved quantity of type
(20).
can make the deterministic equations (16), restriction
equations (17) and additional restriction equations (18) can be established,
meanwhile, there are also
normal functions satisfying the following structural equation (19), then the weak Lie symmetry of discrete
constrained Hamilton systems leads to the discrete conserved quantity of type
(20).
5. Example
The Lagrange function of the system is:
| (21) |
Try to investigate the Lie symmetries and conserved quantities of discrete systems in phase space.
It is
obvious that the L's Hess matrix rank is ![]() , so it is a constrained
Hamilton system, thus there are two constraints in the regular
variables:
, so it is a constrained
Hamilton system, thus there are two constraints in the regular
variables:
| (22) |
The compatibility conditions and stability conditions of the constraints are obtained:
| (23) |
The discrete Hamilton function of the system is as follows:
| (24) |
According to formula (12) and (13), the motion difference equations of the system are obtained:
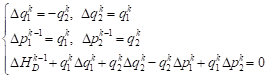 | (25) |
The deterministic equations (16) of Lie symmetry are given:
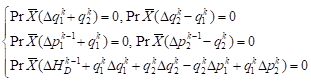 | (26) |
For convenience, we take the standard
lattice, that is, the time step is the equal step length ![]() , then the equations (26) have a set of solutions as follows:
, then the equations (26) have a set of solutions as follows:
| (27) |
The restriction equations (17) are given:
| (28) |
The additional restriction equations (18) are given:
| (29) |
The structural equations (19) give the norm function corresponding to the generating element and it is:
| (30) |
Therefore, the system has the conserved quantity of the corresponding form (20) is:
| (31) |
It is easy to see that the above results are correct, and formula (31) is the discretization of energy conservation in the conservative systems. At the same time, the generating element can be verified to satisfy the restriction equations (28) and the additional restriction equations (29). Therefore, the infinitesimal generating element corresponds to the strong Lie symmetry of the discrete constrained Hamilton systems.
6. Conclusion
The symmetry and conserved quantity of
discrete singular mechanical systems have not yet appeared, in this paper, the
Lie symmetry and the Noether conserved quantity of discrete constrained
Hamilton systems are studied by the difference discrete variational. The main
conclusions are: the differential motion equations (12)
and (13) of discrete constrained Hamilton systems; Lie
symmetry deterministic equations (16) and three definitions for discrete
constrained Hamilton systems; the structural equations and form of the Lie
symmetry leads to a conserved quantity. It is found that the discrete
constrained Hamilton systems have similar forms and properties with the
constrained Hamilton systems under continuous variation when the difference is
regarded as an independent variable, in particular, it can keep the structure
unchanged. An example shows that the results of this paper
can be regarded as a natural generalization to the Lie symmetry of continuous
constrained Hamilton systems ![]() , the conservative discrete singular systems also have energy
conservation. The method and content of this paper can be extended
to study the symmetries and conserved quantities of the nonconservative and
nonholonomic discrete singular mechanical systems in phase space.
, the conservative discrete singular systems also have energy
conservation. The method and content of this paper can be extended
to study the symmetries and conserved quantities of the nonconservative and
nonholonomic discrete singular mechanical systems in phase space.
References
[1] Dirac, P.A.M. (1964). Lecture on Quantum Mechanics. NewYork: Yeshi-va University Press.
[2] Mei, F.X. (1999). The application of Liegroup and Lie algebra to the constrained mechanical systems. Beijing: Science Press (in Chinese).
[3] Noether, E. (1918). Invariante variationsprobleme. Nachr. König. Gesell. Wissen. Göttingen, Math. Phys. KI., 2, 235-257.
[4] Lutzky, M. (1995). Remarks on a recent theorem about conserved quantities. J. Phys. A: Math. Gen., 28(11), 637-638.
[5] Mei, F.X. (2000). Form invariance of Lagrange system. Beijing Institute of Technology, 9(2), 120-124.
[6] Li, Z.P. (1992). The regular form’s generalized Noether theorem of nonholonomic singular systems and its inverse theorem. Huang Huai Journal, 3(1), 8-16 (in Chinese).
[7] Zhang, Y., & Xue, Y. (2001). Lie symmetriesof constraint Hamiltonian system with the second type of constraints. Acta Phys. Sinica, 50(5), 816-819 (in Chinese).
[8] Luo, S.K. (2004). Mei symmetries, Noether symmetries and Lie symmetries of Hamiltonian canonical equations of singular systems. Acta Phys. Sinica, 53(1), 5-11 (in Chinese).
[9] Li, Y.C., Zhang, Y., & Liang, J.H. (2002). Lie symmetries and conservation of a class of nonholonomic singular systems. Acta Phys. Sinica, 51(10), 2186-2190 (in Chinese).
[10] Zheng, M.L. (2017). Perturbation and adiabatic invariants constrained Hamilton of Mei symmetry for system. Journal of Yanbian University (Natural Scicnce), 43(4), 328-335 (in Chinese).
[11] Cadzow, J.A. (1970). Discrete calculus of variations. International Journal of Control, 11(3), 393-407.
[12] Lee, T. (1983). Can time be a discrete dynamical variable. Phys. Lett. B, 122(3), 217-220.
[13] Guo, H.Y., Li, Y.Q, Wu, K., et al. (2002). Difference discrete variational principles, Euler- -Lagrange cohomology and sympletic, multisympletic structures I: difference discretevariational principle. Communications in Theoretical Physics, 37(1), 1-10.
[14] Fu, J.L., Dai, G.D., Salvador, J., & Tang Y.F. (2007). Discrete variational principle and first integrals for Lagrange-Maxwell mechanico-electrical systems. Chin. Phys., 16(3), 570-577.
[15] Fu, J.L., Chen, B.Y., & Chen, L.Q. (2009). Noether symmetries of discrete nonholonomic dynamical systems. Phys. Lett. A, 373(4), 409-412.
[16] Shi, S.Y., Fu, J.L., & Chen, L.Q. (2008). The Lie symmetries and Noether conserved quantities of discrete non-conservative mechanical systems. Chin. Phys. B, 17(2), 385-389.
[17] Dorodnitsyn, V. (1994). Finite difference models entirely inheriting continuous symmetry of original differential equations. Int. J. Mod. Phys. C, 5(04), 723-734.
[18] Lu, K., Fang, J.H., Zhang, M.J., et al. (2009). Noether symmetries and Mei symmetries of discrete holonomic systems in phase space. Acta Phys. Sinica, 58(11), 7421-7426 (in Chinese).
[19] Xu, R.L. (2014). Study on MNL symmetries and new conservation of discrete mechanical systems. Shandong: China University of Petroleum (in Chinese).
[20] Xia, L.L., & Chen L.Q. (2012). Mei symmetries and conserved quantities for non-conservative Hamiltonian difference systems with irregular lattices. Nonlinear Dynamics, 70(2), 1223-1230.
[21] Li, Z.P. (1999). Constrained Hamiltonian system and its symmetric properties. Beijing: Beijing University of Technology Press (in Chinese).


