A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Talibi_2018,
   doi = {10.17512/jamcm.2018.3.08},
   url = {https://doi.org/10.17512/jamcm.2018.3.08},
   year = 2018,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {17},
   number = {3},
   pages = {83--95},
   author = {Boutaina Talibi and  Ahmed Driss Aiat Hadj and  Driss Sarsri},
   title = {A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2018.3.08
UR  - https://doi.org/10.17512/jamcm.2018.3.08
TI  - A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Talibi, Boutaina
AU  - Hadj, Ahmed Driss Aiat
AU  - Sarsri, Driss
PY  - 2018
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 83
EP  - 95
IS  - 3
VL  - 17
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Talibi, B., Hadj, A., & Sarsri, D. (2018). A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix. Journal of Applied Mathematics and Computational Mechanics, 17(3), 83-95. doi:10.17512/jamcm.2018.3.08

Talibi, B., Hadj, A. & Sarsri, D., 2018. A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix. Journal of Applied Mathematics and Computational Mechanics, 17(3), pp.83-95. Available at: https://doi.org/10.17512/jamcm.2018.3.08

[1]B. Talibi, A. Hadj and D. Sarsri, "A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 3, pp. 83-95, 2018.

Talibi, Boutaina, Ahmed Driss Aiat Hadj, and Driss Sarsri. "A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix." Journal of Applied Mathematics and Computational Mechanics 17.3 (2018): 83-95. CrossRef. Web.

1. Talibi B, Hadj A, Sarsri D. A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(3):83-95. Available from: https://doi.org/10.17512/jamcm.2018.3.08

Talibi, Boutaina, Ahmed Driss Aiat Hadj, and Driss Sarsri. "A numerical algorithm for computing the inverse of a Toeplitz pentadiagonal matrix." Journal of Applied Mathematics and Computational Mechanics 17, no. 3 (2018): 83-95. doi:10.17512/jamcm.2018.3.08

A NUMERICAL ALGORITHM FOR COMPUTING THE INVERSE OF A TOEPLITZ PENTADIAGONAL MATRIX

Boutaina Talibi ¹, Ahmed Driss Aiat Hadj ², Driss Sarsri ¹

¹ National School of Applied Sciences, Abdelmalek Essaadi University
Tangier, Morocco
² Regional Center of the Trades of Education and Training (CRMEF)-Tangier, Avenue My Abdelaziz
Souani, BP: 3117, Tangier, Morocco
talibi.boutaina@gmail.com, ait_hadj@yahoo.com, dsarsri@yahoo.fr

Received: 2 August 2018; Accepted: 27 November 2018

Abstract. In the current paper, we present a computationally efficient algorithm for obtaining the inverse of a pentadiogonal toeplitz matrix. Few conditions are required, and the algorithm is suited for implementation using computer algebra systems.

MSC 2010: 15B05 65F40 33C45

Keywords: pentadiagonal matrix, Toeplitz matrix, K-Hessenberg matrix, inverse

1. Introduction

Pentadiagonal Toeplitz matrices often occur when solving partial differential equations numerically using the finite difference method, the finite element method and the spectral method, and could be applied to the mathematical representation of high dimensional, nonlinear electromagnetic interference signals [1-7]. Pentadiagonal matrices are a certain class of special matrices, and other common types of special matrices are Jordan, Frobenius, generalized Vandermonde, Hermite, centrosymmetric, and arrowhead matrices [8-12].

Typically, after the original partial differential equations are processed with these numerical methods, we need to solve the pentadiagonal Toeplitz systems of linear equations for obtaining the numerical solutions of the original partial differential equations. Thus, the inversion of pentadiagonal Toeplitz matrices is necessary to solve the partial differential equations in these cases.

J. Jia, T. Sogabe and M. El-Mikkawy recently proposed an explicit inverse of the tridiagonal Toeplitz matrix which is strictly row diagonally dominant [13]. However, this result cannot be generalized to the case of the pentadiagonal Toeplitz matrix directly. This motivates us to investigate whether an explicit inverse of the pentadiagonal Toeplitz matrix also exists.

In this paper, we present a new algorithm with a totally different approach for numerically inversing a pentadiagonal matrix. Few conditions are required, and the algorithm is suited for implementation using computer algebra systems.

2. Inverse of a Toeplitz pentadiagonal matrix algoritm 1

Definition: We consider the pentadiagonal Toeplitz matrix:

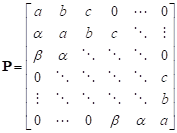Where: . Also and are an arbitrary numbers.

Assume thatis non-singular and denote:

Where are the columns of the inverse .

From the relation . Where denotes the identity matrix of order . We deduce the relations:

(1) for

Where is the vector of order of the canonical basis of .

Consider the sequence of numbers and characterized by a term recurrence relation:

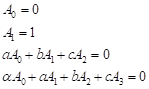(2)

And

for

Also we have:

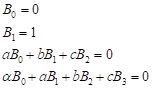(3)

And

for

We can give a matrix form to this term recurrence:

(4)

(5)

Where and .

Let’s define for each

and

(6)

Immediately we have:

and

(7)

Where and .

Lemma: If the matrix is singular.

Proof: If . The is non-null and by (7) we have . We conclude that is singular.

THEOREM 2.1: We supposed that then is invertible. And:

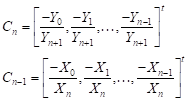(8)

Proof: We have [14]. So is invertible from the relations Equations (7) and (8) we have and . The proof is completed.

Algorithm: New efficient computational algorithm for computing the inverse of the pentadiagonal matrix.

INPUT:

The dimension n.

The arbitrary numbers: and .

OUTPUT:

The inverse matrix

Step 1:

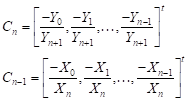Step 2:

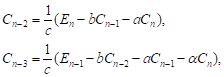Step 3:

for

3. Inverse of a Toeplitz pentadiagonal matrix algoritm 2

Definition: Hessenberg (or lower Hessenberg) matrices are the matrices satisfying the condition for . More generally, the matrix is k-Hessenberg if and only if for .

THEOREM [15]: Let H be a strict-Hessenberg matrix with the block decomposition:

, , , , .

(9)

The H is invertible if and only if is invertible and if H is invertible we have:

(10)

R. Slowik [16] worked in the particular case of the Toeplitz-Hessenberg matrix.

Our work is applied on pentdiagonal matrix of the form:

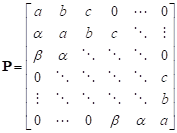(11)

Then we find:

(12)

The blocks , , and are given as:

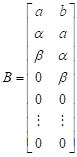(13)

Also:

(14)

(15)

And:

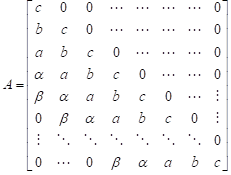(16)

Then the inverse of the matrix will be:

(17)

Where and for .

Proof: Since is a triangular matrix, as well. We prove inductively on n. We have:

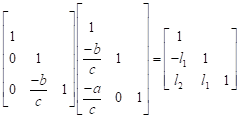(18)

With:

;

(19)

The first step of induction holds.

Consider now . We have

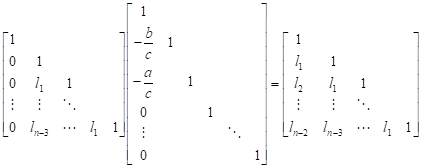(20)

Then:

4. Example

In this section, we give a numerical example to illustrate the effectiveness of our algorithm. Our algorithm is tested by MATLAB R2014a.

Consider the following 7-by-7 pentadiagonal matrix

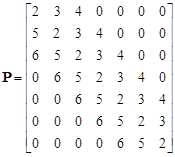(21)

The columns of the inverse are:

, , ,, ,

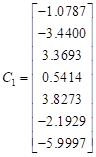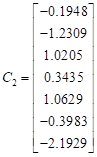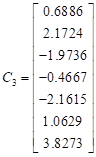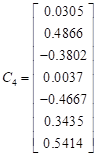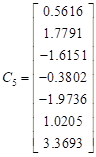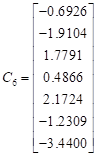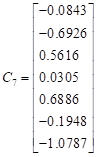Let’s employ the same example and give the blocks A, B, C, and D of the matrix

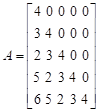(22)

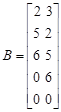(23)

(24)

(25)

Therefore the inverse is:

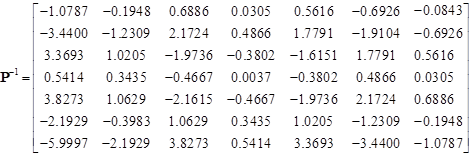(26)

As we can see, the two methods give the same result.

In Table 1 we give a comparison of the running time between the ’Toeplitz- -Hessenberg’ algorithm, our algorithm in MATLAB R2014a and the famous method LU.

The running time (in seconds) of two algorithms in MATLAB R2014a.

Table 1

The running time

5. Conclusions

In this paper, numerical algorithms for computing the inverse of a pentadiagonal Toeplitz matrix are presented. We have showed that the computational cost of our algorithm for finding the inverse of pentadiagonal Toeplitz matrix is much less than those of well-known algorithms. From some numerical examples we have learned that our algorithms work as well as some other well-known algorithms.

Algorithm for Inverse of a Toeplitz pentadiagonal matrix algorithm 1

clear all;
clc;
close all;
s=10;
d = ones(s,1);
P = spdiags([6*d 5*d 2*d 3*d 4*d], -2:2,s ,s );
tic

n=length(P);

b(n)=0;
c(n)=1;c(n-1)=1;
a=diag(P);
b=[diag(P,1); b(n)];
c=[diag(P,2); c(n-1); c(n)];
fa=[0 ;diag(P,-1)];
ta=[0; 0 ;diag(P,-2)];

e1=eye(n);

A0=0;
A(1)=1;
A(2)=(-1/c(1))*(a(1)*A0+b(1)*A(1));
A(3)=(-1/c(2))*(a(2)*A(1)+b(2)*A(2)+fa(2)*A0);
A(4)=(-1/c(3))*(a(3)*A(2)+b(3)*A(3)+fa(3)*A(1)+ta(3)*A0);

for i=4:n
A(i+1)=(-1/c(i))*(a(i)*A(i-1)+b(i)*A(i)+fa(i)*A(i-2)+ta(i)*A(i-3));
end
AA=zeros(n,1);
AA(1)=A0;

for k=2:n
AA(k)=A(k-1);
end

B0=1;
B(1)=0;
B(2)=(-1/c(1))*(a(1)*B0+b(1)*B(1));
B(3)=(-1/c(2))*(a(2)*B(1)+b(2)*B(2)+fa(2)*B0);
B(4)=(-1/c(3))*(a(3)*B(2)+b(3)*B(3)+fa(3)*B(1)+ta(3)*B0);

for i=4:n
B(i+1)=(-1/c(i))*(a(i)*B(i-1)+b(i)*B(i)+fa(i)*B(i-2)+ta(i)*B(i-3));
end

BB=zeros(n,1);
BB(1)=B0;
for k=2:n
BB(k)=B(k-1);
end

Q0=A(n);
for i=1:n-1
QQ(i)=det([ A(n) A(i);B(n) B(i)]) ;
end
Q=[Q0 QQ];
QN=det([ A(n) A(n+1);B(n) B(n+1)]);


R0=A(n+1)*B0;
for i=1:n-1
RR(i)=det([ A(n+1) A(i);B(n+1) B(i)]) ;
end
R=[R0 RR];
RN=det([ A(n+1) A(n);B(n+1) B(n)]) ;

C=zeros(n,n);
C(:,n)=(-1/QN)*Q;
C(:,n-1)=(-1/RN)*R;

C(:,n-2)=(1/c(n-2))*(e1(:,n)-a(n)*C(:,n)-b(n-1)*C(:,n-1));
C(:,n-3)=(1/c(n-3))*(e1(:,n-1)-a(n-1)*C(:,n-1)-b(n-2)*C(:,n-2)-fa(n)*C(:,n));
C(:,n-4)=(1/c(n-4))*(e1(:,n-2)-a(n-2)*C(:,n-2)-b(n-3)*C(:,n-3)-fa(n-1)*C(:,n-1)-ta(n)*C(:,n));
for j=n-3:-1:3
C(:,j-2)=(1/c(j-2))*(e1(:,j)-a(j)*C(:,j)-b(j-1)*C(:,j-1)-fa(j+1)*C(:,j+1)-ta(j+2)*C(:,j+2));
end
%C
%I=C*P
toc

Algorithm for the inverse of a Toeplitz pentadiagonal matrix algorithm 2

References

[1] Aceto, L., Ghelardoni, P., & Magherini, C. (2012). PGSCM: A family of P-stable boundary value methods for second-order initial value problems. J. Comput. Appl. Math., 236, 3857-3868; El-Mikkawy, M., & Karawia, A. (2006). Inversion of general tridiagonal matrices. Appl. Math. Lett., 19, 712720.

[2] Aceto, L., Ghelardoni, P., & Magherini, C. (2012). Boundary value methods for the reconstruction of SturmLiouville potentials. Appl. Math. Comput., 219, 2960-2974; Losiak, J., Neuman, E., & Nowak, J. (1988).The inversion of cyclic tridiagonal matrices. Zastos. Mat., 20(1), 93102.

[3] Kaya, D. (2003). An explicit and numerical solutions of some fifth-order Kdv equation by decomposition method. Appl. Math. Comput., 144, 353-363.

[4] El-Sayed, S.M., & Kaya, D. (2004). An application of the ADM to seven order Sawada Kotara equations. Appl. Math. Comput., 157, 93-101.

[5] Shen, Jie, & Tang, Tao (2006). Spectral and High-Order Methods with Applications. Beijing: Science Press.

[6] Monterde, J., & Ugail, H. (2006). A general 4th-order PDE method to generate Bezier surfaces from the boundary. Comput. Aided Geom. Design, 23, 208-225.

[7] Patil, P.G., & Swamy, Y.S. (2008). An eficient model for vibration control by piezoelectric smart structure using finite element method. Eur. J. Comput. Sci. Netw. Secu., 8, 258-264.

[8] Respondek, J.S. (2011). Numerical recipes for the high efficient inverse of the confluent Vandermonde matrices. Appl. Math. Comput., 218, 2044-2054.

[9] Respondek, J.S. (2013). Recursive numerical recipes for the high efficient inversion of the confluent Vandermonde matrices. Appl. Math. Comput., 225, 718-730.

[10] Li, H., & Zhao, D. (2014). An extension of the Golden-Thompson theorem. J. Inequal. Appl.

[11] Li, H.Y., Gong, Z.G., & Zhao, D. (2014). Least squares solutions of the matrix equation AXB+CYD=E with the least norm for symmetric arrowhead matrices. Appl. Math. Comput., 226, 719-724.

[12] Wang, Chaojie, Li, Hongyi, & Zhao, Di (2015). An explicit formula for the inverse of a penta-diagonal Toeplitz matrix. Journal of Computational and Applied Mathematics, 278, 12-18.

[13] Hadj, A., & Elouafi, M. (2008). A fast numerical algorithm for the inverse of a tridiagonal and pentadiagonal matrix. Appl. Math. Comput., 202, 441-445.

[14] Hadj, D.A., & Elouafi, M. (2008). The characteristic polynomial, eigenvectors and determinant of a pentadiagonal matrix. Appl. Math. Comput., 198(2), 634-642.

[15] Verde-Star, L. (2015). Elementary triangular matrices and inverses of k-Hessenberg and triangular matrices. Spec. Matrices, 3, 250256.

[16] Slowik, R. (2018). Inverses and determinants of Toeplitz-Hessenberg matrices. Taiwanese Journal of Mathematics, 22, 4, 901-908.