Multiline queueing system with random time limitations and limited buffer space
Oleg Tikhonenko
,Paweł Zając
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
 View in HTML format |
 Export citation |
@article{Tikhonenko_2018,
doi = {10.17512/jamcm.2018.4.10},
url = {https://doi.org/10.17512/jamcm.2018.4.10},
year = 2018,
publisher = {The Publishing Office of Czestochowa University of Technology},
volume = {17},
number = {4},
pages = {99--106},
author = {Oleg Tikhonenko and Paweł Zając},
title = {Multiline queueing system with random time limitations and limited buffer space},
journal = {Journal of Applied Mathematics and Computational Mechanics}
}TY - JOUR DO - 10.17512/jamcm.2018.4.10 UR - https://doi.org/10.17512/jamcm.2018.4.10 TI - Multiline queueing system with random time limitations and limited buffer space T2 - Journal of Applied Mathematics and Computational Mechanics JA - J Appl Math Comput Mech AU - Tikhonenko, Oleg AU - Zając, Paweł PY - 2018 PB - The Publishing Office of Czestochowa University of Technology SP - 99 EP - 106 IS - 4 VL - 17 SN - 2299-9965 SN - 2353-0588 ER -
Tikhonenko, O., & Zając, P. (2018). Multiline queueing system with random time limitations and limited buffer space. Journal of Applied Mathematics and Computational Mechanics, 17(4), 99-106. doi:10.17512/jamcm.2018.4.10
Tikhonenko, O. & Zając, P., 2018. Multiline queueing system with random time limitations and limited buffer space. Journal of Applied Mathematics and Computational Mechanics, 17(4), pp.99-106. Available at: https://doi.org/10.17512/jamcm.2018.4.10
[1]O. Tikhonenko and P. Zając, "Multiline queueing system with random time limitations and limited buffer space," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 4, pp. 99-106, 2018.
Tikhonenko, Oleg, and Paweł Zając. "Multiline queueing system with random time limitations and limited buffer space." Journal of Applied Mathematics and Computational Mechanics 17.4 (2018): 99-106. CrossRef. Web.
1. Tikhonenko O, Zając P. Multiline queueing system with random time limitations and limited buffer space. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(4):99-106. Available from: https://doi.org/10.17512/jamcm.2018.4.10
Tikhonenko, Oleg, and Paweł Zając. "Multiline queueing system with random time limitations and limited buffer space." Journal of Applied Mathematics and Computational Mechanics 17, no. 4 (2018): 99-106. doi:10.17512/jamcm.2018.4.10
MULTILINE QUEUEING SYSTEM WITH RANDOM TIME LIMITATIONS AND LIMITED BUFFER SPACE
Oleg Tikhonenko1, Paweł Zając2
1
Faculty of Mathematics and Natural Sciences, College of Sciences
Cardinal Stefan Wyszyński University in Warsaw
Warsaw, Poland
2 Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
o.tikhonenko@uksw.edu.pl, pawel_zajac@vp.pl
Received: 3 April 2018; Accepted: 17 January 2019
Abstract. In the paper, we investigate multi-server queueing systems with demands of random space requirements (volumes), in which buffer space is limited by constant value and queueing ore (and) service time are limited by exponentially distributed random variables. For such systems, stationary demands number distribution and loss probability are determined. Some numerical results are attached as well.
MSC 2010: 90B22, 60K25, 68M20
Keywords: total demands volume, system buffer capacity, loss probability, Stieltjes convolution
1. Introduction
Queueing systems with demands of a random space requirement (or random volume) [1, 2] are the generalization of the classical queueing models [3, 4]. They can be used to model and solve various practical problems in the design of computer and communication systems (see e.g. [1, 2, 5]). In particular, such models can be applied to buffer space volume determination in the nodes of computer and communication networks. The main proposition of the theory of such systems [1] is the heterogeneity of demands served by the system with respect to their random volumes, in other words, we propose that different demands need different memory size (volume) during their presence in the system.
In the paper, we investigate queueing systems in which demands are also “impatient”, i.e. they can leave the system during their waiting in the queue or (and) during their servicing. In the classical queueing theory (for demands without random volume), systems with times limitations were investigated e.g. in [4, 6]. In particular, in [6] queueing systems with random limitations of queueing and (or) service time were investigated. In the paper [7], the system with random volume demands, deterministically limited total demands volume and deterministically limited queueing or sojourn time were analyzed.
In this paper, we investigate a similar system, but the difference is that, in the system under consideration, queueing and (or) service time are limited by exponen- tially distributed random variables. For example, we have a situation when a demand contains some information that can be grown old fore random reasons, and therefore it must be eliminated from the system.
The paper is organized as follows: In the Section 2, we give the mathematical description of the model and introduce some necessary notations. In Section 3, we introduce the functions describing the system behavior and define an appropriate Markov process. In Section 4, we build a system of differential equations for the function introduced in Section 3 and give its steady-state solution, from which the steady-state demands number distribution is determined. In Section 5, we determine the loss probability for the system under consideration. Section 6 contains examples of numerical results illustrating theoretical formulas, and the last Section 7 presents conclusions and final remarks.
2. Model description
We consider a queueing system of M/M/n/m![]() -type, in which all demands
are characterized by some random
volume (or space requirement)
-type, in which all demands
are characterized by some random
volume (or space requirement) ![]() , where
, where ![]() is
a non-negative random variable that doesn’t depend on
the volumes of other
demands and the epoch of the demand’s entering to the system. Denote by
is
a non-negative random variable that doesn’t depend on
the volumes of other
demands and the epoch of the demand’s entering to the system. Denote by ![]() the distribution function of
the random variable
the distribution function of
the random variable ![]() Let
Let ![]() be the total
demands volume or the sum of all volumes of demands present in the system at time instant t. The values of the
random process
be the total
demands volume or the sum of all volumes of demands present in the system at time instant t. The values of the
random process ![]() are bounded by the con-
stant value V (
are bounded by the con-
stant value V (![]() ) named the system buffer capacity. Let
) named the system buffer capacity. Let ![]() be the number of demands present in the system at time instant t.
be the number of demands present in the system at time instant t.
If a demand of volume x arrives to the
system at epoch t when there are ![]() other demands in it and
other demands in it and ![]() we have
we have ![]()
![]() and the demand is accepted to
the system. In opposite case (
and the demand is accepted to
the system. In opposite case (![]() ), the demand will be lost without
influence to future system behavior. In this case, we have
), the demand will be lost without
influence to future system behavior. In this case, we have ![]()
![]() The arriving demand will be lost also if
there are
The arriving demand will be lost also if
there are ![]() other demands at the epoch t.
other demands at the epoch t.
Demands accepting to the system are served in
accordance to FIFO discipline. But their queueing time and (or) sojourn time
are limited by some random variables having an exponential distributions with
parameters ![]() and
and ![]() respectively,
i.e. demands can leave the system (be lost) during waiting in the queue or
servic-
ing. In particular, if only queueing
time is limited in the system, we have
respectively,
i.e. demands can leave the system (be lost) during waiting in the queue or
servic-
ing. In particular, if only queueing
time is limited in the system, we have ![]() if only service time is
limited, we have
if only service time is
limited, we have ![]() and if sojourn time is limited in
the system, we obtain
and if sojourn time is limited in
the system, we obtain ![]() Let a be the parameter of demands enter
flow,
Let a be the parameter of demands enter
flow, ![]() be the
parameter of service time (we assume that service time doesn’t depend on the demand volume). We
also assume that the traffic load of the system
be the
parameter of service time (we assume that service time doesn’t depend on the demand volume). We
also assume that the traffic load of the system ![]() is finite (
is finite (![]() ).
).
Our aim is the determination of the steady-state distribution of number of demands present in the system and the demand loss probability.
3. Process and characteristics
The behavior of the system under consideration can be described by the following Markov random process
| (1) |
where ![]() is the
volume of the j-th demand presenting in the system at time
instant t. It is clear that
is the
volume of the j-th demand presenting in the system at time
instant t. It is clear that ![]()
The process (1) we shall characterize by the functions having the following probability sense:
| (2) |
| (3) |
| (4) |
It is clear that, for ![]() we
have
we
have ![]()
4. Steady-state distribution of demands present in the system
It can be easily shown that the functions (2)-(4) satisfy the following Kolmogorov-type equations (see also [8] for comparison):
| (5) |
| (6) |
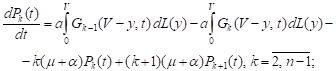 | (7) |
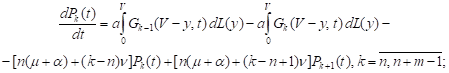 | (8) |
| (9) |
Assume that at
least one of the values m and V is finite. Then, we have obviously that ![]() when
when ![]() in
the sense of a weak convergence, where the random variables
in
the sense of a weak convergence, where the random variables ![]() and
and ![]() are the steady-state number of demands present
in the system and their total volume, consequently. So, the following
finite limits exist:
are the steady-state number of demands present
in the system and their total volume, consequently. So, the following
finite limits exist:
| (10) |
| (11) |
We have evidently ![]() for
for ![]()
It follows from the equations (5)-(9) that the steady-state characteristics (10) and (11) satisfy the following equations:
| (12) |
| (13) |
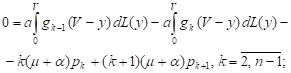 | (14) |
 | (15) |
| (16) |
Introduce the following notation for the
Stieltjes convolution of the distribution function ![]() :
: ![]()
![]()
![]() .
.
Then, by direct substitution, we can easily show that the solution of the Eqs. (12)-(16) has the form:
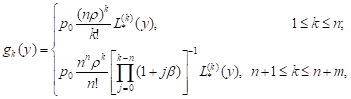 | (17) |
where ![]()
We have from the relations (17) that
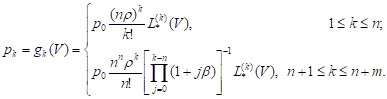 | (18) |
The probability ![]() can
be determined from the normalization condition
can
be determined from the normalization condition ![]() whereas
we obtain:
whereas
we obtain:
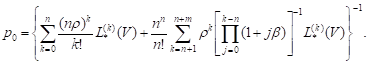 |
5. Loss probability
Let A be the event that an arbitrary
arriving demand is accepted to the system
and served completely and K be the mean number
of busy servers in steady state. We have evidently that ![]() and
we obtain for probability of the event A:
and
we obtain for probability of the event A: ![]() Then,
the probability that an arbitrary demand is lost at its arriving epoch or is
not served completely can be determined as
Then,
the probability that an arbitrary demand is lost at its arriving epoch or is
not served completely can be determined as ![]()
![]()
6. Numerical examples
In this section, we present numerical
examples illustrating theoretical results. More precisely, we present how the
loss probability ![]() depends on the buffer
capacity V and the parameters
depends on the buffer
capacity V and the parameters ![]() Assume that the
volumes of entering
demands are exponentially distributed with parameter
Assume that the
volumes of entering
demands are exponentially distributed with parameter ![]() and
service time has
an exponential distribution with parameter
and
service time has
an exponential distribution with parameter ![]() Consider
three cases of the considered system when
Consider
three cases of the considered system when ![]() (a
single-server system).
(a
single-server system).
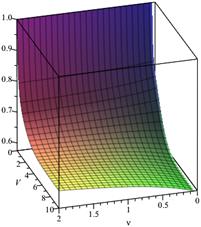
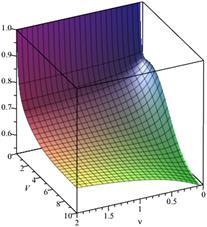
Fig.
1. Loss probability, ![]() ,
, ![]() Fig.
2. Loss probability,
Fig.
2. Loss probability, ![]() ,
, ![]() ,
, ![]()
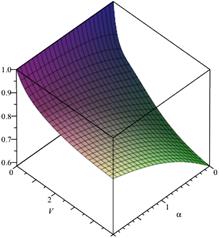
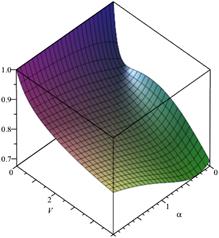
Fig.
3. Loss probability, ![]() ,
,![]() Fig. 4. Loss probability,
Fig. 4. Loss probability, ![]() ,
, ![]() ,
, ![]()
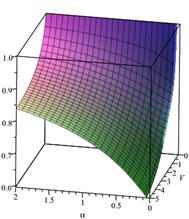
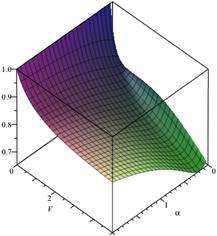
Fig.
5. Loss probability, ![]() ,
, ![]() Fig. 6. Loss probability,
Fig. 6. Loss probability, ![]() ,
, ![]() ,
, ![]()
In the first case (Figs. 1 and 2), only
the queueing time is limited, i.e. we have ![]() Assume
that the system buffer capacity V takes the values from 0 to 10,
and the parameter
Assume
that the system buffer capacity V takes the values from 0 to 10,
and the parameter ![]() takes the values from 0 to 2.
Furthermore, when
takes the values from 0 to 2.
Furthermore, when ![]() and
and ![]() ,
then
,
then ![]() and
and ![]() . For
example, if there is one waiting place in the queue (
. For
example, if there is one waiting place in the queue (![]() ),
then, for
),
then, for ![]() and
and ![]() the
loss probability
the
loss probability ![]() is equal to 0.68765 (Fig. 1).
If
is equal to 0.68765 (Fig. 1).
If ![]() , then
, then ![]() (Fig.
2).
(Fig.
2).
In the second case, only service time is
limited (Figs. 3 and 4), then we have ![]() Assume
that the system buffer capacity V takes the values from 0 to 5, and the
parameter
Assume
that the system buffer capacity V takes the values from 0 to 5, and the
parameter ![]() takes the values from 0 to 2.
Furthermore, when
takes the values from 0 to 2.
Furthermore, when ![]() and
and ![]() ,
then
,
then ![]() and
and ![]() . For example, if the queue size is 1 (
. For example, if the queue size is 1 (![]() ), for
), for ![]() and V = 1,
the loss probability
and V = 1,
the loss probability ![]() 0.898072 (Fig. 3).
If
0.898072 (Fig. 3).
If ![]() , then we have
, then we have ![]() 0.8985
(see Fig. 4).
0.8985
(see Fig. 4).
In the third case, the sojourn time of demand
in the system is limited, then we assume ![]() (Figs. 5
and 6). Assume that V takes the values from 0 to 5 and
(Figs. 5
and 6). Assume that V takes the values from 0 to 5 and ![]() takes values from 0 to 2.
In addition, when
takes values from 0 to 2.
In addition, when ![]() and
and ![]() ,
we have
,
we have ![]() and
and ![]() . For
example, if there is one waiting place
in the queue (
. For
example, if there is one waiting place
in the queue (![]() ), for
), for ![]() and
and
![]() we have
we have ![]() 0.898516
(Fig. 5).
If
0.898516
(Fig. 5).
If ![]() , then
, then ![]() 0.898603
(Fig. 6).
0.898603
(Fig. 6).
7. Conclusions
In the paper, we consider a multiline queueing system with random time limitations and limited buffer space. The determination of the steady-state distribution of number of demands present in the system and the demand loss probability are presented. Some special cases of the system under consideration are provided with numerical calculations in Maple. In any case, when the number of waiting places increases, of course the loss probability of demand also increases. This model shows the loss probability of demand (see Figs. 1-6). The results obtained in the paper can be used for estimating of total demands volume characteristics in the nodes of computer and telecommunication networks.
References
[1] Tikhonenko, O. (2006). Probability Methods of Information System Analysis. Warsaw: Akade-micka Oficyna Wydawnicza EXIT (in Polish).
[2] Tikhonenko, O.M. (1990). Queueing Models in Information Systems (Modeli massovogo obsluzhivanija v sistemah obrabotki informacii). Minsk: Universitrtskoe (in Russian).
[3] Bocharov, P.P., D’Apice, C., Pechinkin, A.V., & Salerno, S. (2004). Queueing Theory. Utrecht- -Boston: VSP.
[4] Gnedenko, B.V., & Kovalenko, I.N. (1989). Introduction to Queueing Theory. Boston: Birkhäuser.
[5] Naumov, V.A., & Samouylov, K.E. (2016). On relationship between queueing systems with resources and Erlang networks. Informatics and Applications (Informatika i ee Primeneniya), 10, 3, 9-14 (in Russian).
[6] Ovcharov, L.A. (1969). Applied Queueing Theory (Prikladnye zadachi teorii massovogo obsluzhivanija). Moscow: Mashinostrojenie (in Russian).
[7] Tikhonenko, O., & Zając, P. (2017). Queueing systems with demands of random space requirement and limited queueing or sojourn time. Communications in Computer and Information Science, 718, 380-391.
[8] Alexandrov, A.M., & Kaz, B.A. (1973). Non-homogeneous demands flows service. Izvestiya AN SSSR. Tekhnicheskaya Kibernetika, 2, 47-53 (in Russian).


