High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures

• BibTex
• RIS
• APA
• Harvard
• IEEE
• MLA
• Vancouver
• Chicago

@article{Garus_2018,
   doi = {10.17512/jamcm.2018.4.03},
   url = {https://doi.org/10.17512/jamcm.2018.4.03},
   year = 2018,
   publisher = {The Publishing Office of Czestochowa University of Technology},
   volume = {17},
   number = {4},
   pages = {19--24},
   author = {Sebastian Garus and  Wojciech Sochacki},
   title = {High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures},
   journal = {Journal of Applied Mathematics and Computational Mechanics}
}

TY  - JOUR
DO  - 10.17512/jamcm.2018.4.03
UR  - https://doi.org/10.17512/jamcm.2018.4.03
TI  - High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures
T2  - Journal of Applied Mathematics and Computational Mechanics
JA  - J Appl Math Comput Mech
AU  - Garus, Sebastian
AU  - Sochacki, Wojciech
PY  - 2018
PB  - The Publishing Office of Czestochowa University of Technology
SP  - 19
EP  - 24
IS  - 4
VL  - 17
SN  - 2299-9965
SN  - 2353-0588
ER  - 

Garus, S., & Sochacki, W. (2018). High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures. Journal of Applied Mathematics and Computational Mechanics, 17(4), 19-24. doi:10.17512/jamcm.2018.4.03

Garus, S. & Sochacki, W., 2018. High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures. Journal of Applied Mathematics and Computational Mechanics, 17(4), pp.19-24. Available at: https://doi.org/10.17512/jamcm.2018.4.03

[1]S. Garus and W. Sochacki, "High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures," Journal of Applied Mathematics and Computational Mechanics, vol. 17, no. 4, pp. 19-24, 2018.

Garus, Sebastian, and Wojciech Sochacki. "High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures." Journal of Applied Mathematics and Computational Mechanics 17.4 (2018): 19-24. CrossRef. Web.

1. Garus S, Sochacki W. High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures. Journal of Applied Mathematics and Computational Mechanics. The Publishing Office of Czestochowa University of Technology; 2018;17(4):19-24. Available from: https://doi.org/10.17512/jamcm.2018.4.03

Garus, Sebastian, and Wojciech Sochacki. "High-performance quasi one-dimensional mirrors of mechanical waves built of periodic and aperiodic structures." Journal of Applied Mathematics and Computational Mechanics 17, no. 4 (2018): 19-24. doi:10.17512/jamcm.2018.4.03

HIGH-PERFORMANCE QUASI ONE-DIMENSIONAL MIRRORS OF MECHANICAL WAVES BUILT OF PERIODIC AND APERIODIC STRUCTURES

Sebastian Garus, Wojciech Sochacki

Institute of Mechanics and Machine Design Fundamentals
Czestochowa University of Technology
Częstochowa, Poland
gari.sg@gmail.com, w.sochacki@imipkm.pcz.pl

Received: 24 July 2018; Accepted: 27 October 2018

Abstract. The work studied the reflectance for quasi one-dimensional phononical structures. In composite superlattices, the thickness of the layers, their arrangement and selection of constituent materials with appropriate properties such as the density and velocity of mechanical waves propagation allows for the creation of a phononic band gap (PhBG) phenomenon. PhBG is characterized by high reflectance of the mechanical wave incident on the analyzed structure, which means that the wave does not propagate in the superlattice. The paper proposes periodic and aperiodic structures characterized by a wide range of reflectance for the ultrasonic frequencies of mechanical waves and shows how the change the thickness of the layer affects the properties of the analyzed structures.

MSC 2010: 03G10, 51G05, 65F30, 65Z05, 74J20, 74S30

Keywords: mechanical waves, phononic, reflectance, transfer matrix, band gap

1. Introduction

Among composite materials, it is possible to create structures in which waves with given frequencies will not propagate. These structures can be one (1D), two (2D) and three-dimensional (3D) [1]. The phenomenon of no propagation of waves at given frequencies is called the occurrence of a phononic band gap [2].

The design in the 1-D of the multilayer structure in order to obtain a band gap can be achieved by changing the phononic superlattice geometry. A similar effect is obtained by changing the elastic characteristics of constitutive materials using external stimulation [3].

Phononic crystals show in their band structures frequency ranges forbidden to propagate elastic waves. These crystals, characterized by a phononic band gap occurrence, have many practical applications. They can be used to build sound shields and filters [4], acoustic focusing of sound [5] or acoustic interferometers [6]. In addition, phononic crystals found application in the construction of selective frequency waveguides [7] or for the construction of an acoustic diode [8].

In this work, the Transfer Matrix Method algorithm (TMM) was used for the determination of the reflectance coefficient for elastic waves propagation in a phononic crystal. The TMM algorithm was used in the work [9] to obtain the transmission coefficient for the quasi one-dimensional Severin aperiodic multilayer. This method was also used in [10] to analyze the occurrence of characteristic peaks in phononic multilayer structures.

The work was considered periodic - binary, quasi periodic - Thue-Morse and aperiodic - Severin multilayer structures. The three mentioned types of structures were analyzed in the work, [11] and the transmission characteristics of structures with defects were obtained.

The paper proposes structures characterized by a wide range of reflectance for the ultrasonic frequencies of mechanical waves and shows how the change in material parameters affects the properties of the analyzed structures. The existence of reflectance bands with full wave reflection for these structures was presented.

2. Transfer Matrix Method algorithm

The propagation of the wave in a multilayer structure can be described by the matrix equation

(1)

where is pressure of incident mechanical wave, reflected, transmitted wave and is always 0. M is a characteristic matrix depending on the layers structure. The characteristic matrix M for n-elements multilayer structure takes the form

(2)

In the multilayer structure, the transition between the layers is described by matrix Φ_i,i+1 and propagation matrix matrix Γ_i, corresponding to the i-layer with thickness d_i, which is given by

,

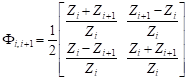(3)

The wave vector is determined by and the acoustic impedance i-layer is defined as for frequency f, phase velocity v and mass density ρ.

The reflection coefficient R of the multilayer aperiodic structure was determined from the characteristic matrix M and denoted as

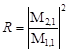(4)

3. Research

The tests were carried out for three types of structures: periodic - binary, quasi periodic - Thue-Morse and aperiodic - Severin. Their characteristics including: type, initial conditions and creation rules were presented in Table 1.

Table 1. Structures types and building rules

The distribution of layers (A, B) into individual structures for the L (2-5) generations number were collected in Table 2.

Table 2. Arrangement of the layers of structures for L generations number

The material of the layers consisted respectively of: A - Epoxy and B - Glass. The material properties of the structure layers have been shown in Table 3. On the basis of numerical calculations, reflection coefficients in the frequency range (0¸1000 kHz) were obtained for the considered structures. Reflectance (R) maps for different types of structures in which the thickness of layer B (dB) was increased from the determined base value to three times its value were presented in Figures 1-3.

Table 3. Material parameters of the components of the multilayer structure [12, 13]

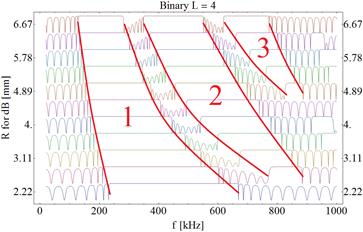
Fig. 1. Reflectance maps for a Binary structure in which the thickness of layer B was increased. High reflectance bands are marked

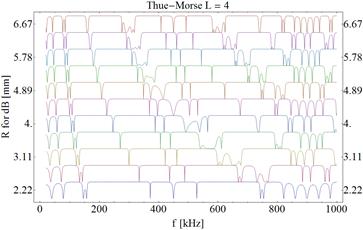
Fig. 2. Reflectance maps for a Thue-Morse structure in which the thickness of layer B was increased

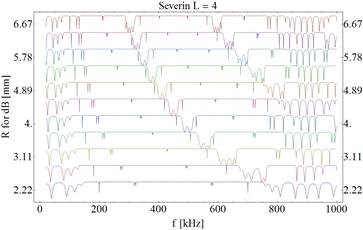
Fig. 3. Reflectance maps for a Severin structure in which the thickness of layer B was increased

Further graphs of reflectance for each thickness of the layer B is shifted by the full transmission. In each of the three analyzed cases, high reflectance bands can be distinguished. In the first band (Fig. 1), as the layer thickness B (dB) increases, its width decreases and moves towards the lower frequencies. The offset is also noticeable for the other two bands. However, there was no clear relationship between the thickness of the B layer and the width of individual bands. For the base value of the thickness of layer B, the band 2 does not occur. Three bands are also visible in Thue-Morse (Fig. 2) and Severin (Fig. 3) structures, but they are wider than in the binary structure and are intersected by high transmission peaks.

4. Conclusions

In the work, the reflectance coefficient was investigated for three types of structures with the same number of layers. The structures were respectively: periodic - binary, quasi periodic - Thue-Morse, aperiodic - Severin. The existence of reflectance bands with full wave reflection has been shown. As the thickness of the B layer increased, the reflectance band thicknesses declined (only at first band) and they moved towards the lower frequencies (all bands). Unlike the other structures, there were no transmission peaks inside the reflectance bands in the binary superlattice. In particular, the Thue-Morse structure can be used as a selective filter due to the high transmission peaks inside the bandgaps. A change of one of the materials for the piezoelectric layers would, to some extent, control the positions of the voltage peaks.

References

[1] Armenise, M.N., Campanella, C.E., Ciminelli, C., Dell’Olio, F., & Passaro, V.M.N. (2010). Phononic and photonic band gap structures: modelling and applications. Physics Procedia, 1(3), 357-364, DOI: 10.1016/j.phpro.2010.01.047.

[2] Sanchis, L., Cervera, F., Sánchez-Dehesa, J., Sánchez-Pérez, J.V., Rubio, C., & Mártinez-Sala, R. (2001). Reflectance properties of two-dimensional sonic band-gaps crystals. Journal of the Acoustical Society of America, 109, 2598-2605.

[3] Nowak, P., & Krawczyk, M. (2010). Phononic band gaps in one-dimensional phononic crystals with nanoscale periodic corrugations at interfaces. FDTD and PWM simulations. Computational Method in Science and Technology, 16(1), 85-95.

[4] Torres, M., Montero de Espinosa, F.R., & Aragon, J.L. (2001). Ultrasonic wedges for elastic wave bending and splitting without requiring a full band gap. Physical Review Letters, 86, 4282-4285.

[5] Cervera, F., Sanchis, L., Sanchez-Perez, J.V., Martinez-Sala, R., Rubio, C., Meseguer, F., Lopez, C., Caballero, D., & Sanchez-Dehesa, J. (2002). Refractive acoustic devices for airborne sound. Physical Review Letters, 88, 23902-23906.

[6] Sanchis, L., Hakansson, A., Cervera, F., & Sanchez-Dehesa, J. (2003). Acoustic interferometers based on two-dimensional arrays of rigid cylinders in air. Physical Review, 67, 35422-1-35422-11.

[7] Khelif, A., Deymier, P.A., Djafari-Rouhani, B., Vasseur, J.O., & Dobrzynski, L. (2003). Two-dimensional phononic crystal with tunable narrow pass band: application to a waveguide with selective frequency. Journal of Applied Physics, 94, 1308-1311.

[8] Liang, B., Yuan, B., & Cheng, J.-C. (2009). Acoustic diode: rectification of acoustic energy flux in one-dimensional systems. Physical Review Letters, 103, 104301-104305.

[9] Garus, S., & Sochacki, W. (2017). One dimensional phononic FDTD algorithm and Transfer Matrix Method implementation for Severin aperiodic multilayer. Journal of Applied Mathematics and Computational Mechanics, 16(4), 17-27.

[10] Garus, S., Sochacki, W., & Bold, M. (2018). Comparison of phononic structures with piezo- electric 0.62PB(MG1/3NB1/3)O3-0.38PBTIO3 defect layers. Engineering Mechanics 2018, Svratka, Czech Republic, 229-232, DOI: 10.21495/91-8-229.

[11] Garus, S., & Szota, M. (2018). Occurence of characteristic peaks in phononic multilayer structures. Revista de Chimie, 69(3), 735-738.

[12] Wang, Y., Song, W., Sun, E., Zhang, R., & Cao, W. (2014). Tunable passband in one-dimen-sional phononic crystal containing a piezoelectric 0.62Pb(Mg1/3Nb2/3)O3–0.38PbTiO3 single crystal defect layer, Physica E: Low-dimensional Systems and Nanostructures 60, 37-41.

[13] Villa-Arango, S., Torres Villa, R., Kyriacou, P.A., Lucklum, R. (2016). Cavity resonance sensor with disposable analyte container for point of care testing. IEEE Sensors Journal, 16, 17, 6727-6732, DOI: 10.1109/JSEN.2016.2584240.