An example of non-Keller mapping



AN EXAMPLE OF NON-KELLER MAPPING

Edyta Pawlak ¹, Sylwia Lara-Dziembek ¹, Grzegorz Biernat ¹ Magdalena Woźniakowska ²

¹ Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
² Faculty of Mathematics and Computer Science, University of Lodz
Łódź, Poland
edyta.pawlak@im.pcz.pl, sylwia.lara@im.pcz.pl, grzegorz.biernat@im.pcz.pl magdalena_wozniakowska@wp.pl

Abstract. In the paper a nontrivial example of non-Keller mapping is considered. It is shown that the Jacobian of rare mapping, having one zero at infinity, being constant must vanish.

Keywords: Jacobian, zero at infinity, rare mappings, Keller mappings

1. Introduction

In this paper we consider the rare polynomial mappings of two complex variables. We study the mappings having one zero at infinity [1-3]. We prove that if the Jacobian of this mapping is constant, it must be zero. The work concerns the problems related to the Keller mappings [4-6]. Recall that the Keller mapping is a polynomial mapping satisfies the condition . In this work, non-Keller mapping are those whose the Jacobian being constant must vanish.

2. The rare mappings

Let be the complex polynomials of degrees 2k + 1 and 2k, consequently, and having one zero at infinity. We consider the rare mappings, i.e. the mappings, whose number of zero forms following the leading form is not more than k – 1. In our case, the mapping has exactly k – 1 zero forms.

Therefore, we can write

(1)

and

(2)

where and are the forms indicated degrees.

3. Basic lemma

At the beginning let us provide the following property:

Property. If , then .

Proof.

Must be

(3)

Therefore

(4)

and since , so

We assume

(5)

Let’s prove that

Lemma. Really, with the given assumptions, we have

Proof. Let

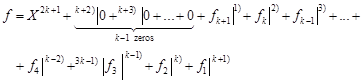(6)

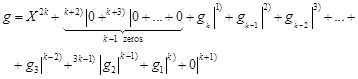(7)

Since the Jacobian is constant, we have in sequence

(8)

so

(9)

and next

(10)

therefore

(11)

and

(12)

however

(13)

etc.

Finally in the step k) we have

(14)

so

(15)

Now, an important step

(16)

where according to the formula (9) we have

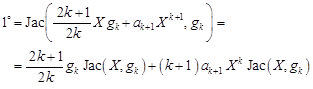(17)

Returning to the formula (16) we obtain

(18)

then

(19)

This means that

(20)

so, according to the Property, we obtain

(21)

and reusing the formula (19) we have

(22)

In the next step we receive

(23)

where according to the formulas (21) and (11) we get

(24)

and

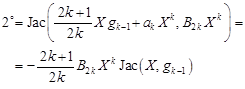(25)

Returning to the formula (23) we have

(26)

Let’s

(27)

We consider two cases:

(I)

Then

(28)

In the next steps we receive in sequence

(29)

so

(30)

etc.

Finally, in the step 2k) we have

(31)

Thus, according to the formula (22) we obtain

(32)

what concludes the proof in the first case.

(II)

Then in the step k + 3) we get

(33)

So using the formulas (11), (13), (21) and (28) we have

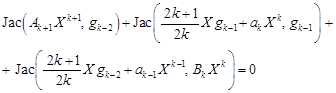(34)

hence

(35)

and

(36)

therefore

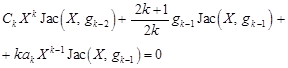(37)

Because C_k = 0, then

(38)

Consequently

(39)

In the following steps, depending on the obtained values of the coefficients (non-zero or zero), we obtain the successive values of the forms

(40)

When all the subsequent coefficients are zero, in step 3k – 1) we have

(41)

Thus, according to the formula (22) we obtain

(42)

which ends the proof in the second case.

4. Conclusion

In this article we consider the “frontier” case of rare and non-Keller mapping. Increasing the number of zeros trivializes the calculation and the reduction significantly complicates them. Even so, we believe that we can reduce the number of zeros.

Algorithms reducing the number of zeros seem to be difficult, as we mentioned earlier. It is sufficient to consider the case when the number of zeros equals k – 2. The algorithms reducing the number of zeros will be presented in future articles.

References

[1] Griffiths P., Harris J., Principles of Algebraic Geometry, New York 1978.

[2] Mumford D., Algebraic Geometry I: Complex Projective Varieties, Springer-Verlag, New York 1975.

[3] Shafarevich I.R., Basic Algebraic Geometry, Springer-Verlag, Berlin, New York 1974.

[4] Wright D., On the Jacobian conjecture, Illinois J. Math. 1981, 25, 3, 423-440.

[5] Van den Essen A., Polynomial Automorphisms and the Jacobian Conjecture, Progress in Mathe- matics 190, Birkhäuser Verlag, Basel 2000.

[6] Bass H., Connell E.H., Wright D., The Jacobian conjecture: reduction of degree and formal expansion of the inverse, American Mathematical Society. Bulletin. New Series 1982, 7(2), 287-330.