Application of second order inhomogeneous linear recurrences to solving a tridiagonal system
Jolanta Borowska
,Lena Łacińska
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
APPLICATION OF SECOND ORDER INHOMOGENEOUS LINEAR RECURRENCES TO SOLVING A TRIDIAGONAL SYSTEM
Jolanta Borowska, Lena Łacińska
Institute of Mathematics, Czestochowa University of
Technology
Częstochowa, Poland
jolanta.borowska@im.pcz.pl, lena.lacinska@im.pcz.pl
Abstract. In this paper we consider a linear system of algebraic equations of a tridiagonal type. We show that the solution of such a system can be represented by a corresponding second order inhomogeneous linear recurrence equation. This approach enables us to represent the solution to the tridiagonal Toeplitz linear system of equations in a closed form.
Keywords: tridiagonal system, linear recurrence equations
1. Introduction
The subject of considerations is a tridiagonal linear system of algebraic equations. Such a system comes up in a variety of scientific topics, see for example [1, 2]. The literature related to algorithms for solving tridiagonal linear systems is very wide. The most known are those based on the Thomas method. The new symbolic algorithm and the review of the literature on this subject can be found in [3].
The aim of this paper is to show that the solution to a tridiagonal linear system of algebraic equations can be represented by a corresponding second order inhomogeneous linear recurrence equation with variable coefficients. This approach enables us to obtain a closed form of solution in the case of Toeplitz tridiagonal system.
A linear algebraic tridiagonal system for n unknowns can be represented by a matrix equation of the form
| (1) |
where
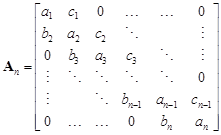 , , 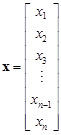 , , 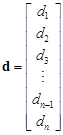 | (2) |
Let us observe that equation (1) may be written as
| (3) |
where ![]() and
and ![]() .
.
In
this paper it will be assumed that the matrix ![]() is
nonsingular. This means that linear system (1) has a
unique solution.
is
nonsingular. This means that linear system (1) has a
unique solution.
2. Main results
Let us denote a determinant of matrix ![]() by
by ![]() . In
the subsequent considerations it will be assumed that
. In
the subsequent considerations it will be assumed that ![]() .
The linear recurrence equation that represents determinant
.
The linear recurrence equation that represents determinant ![]() was shown for example in [4]. Bearing
in mind these results, we have
was shown for example in [4]. Bearing
in mind these results, we have
| (4) |
By
![]() we denote a determinant of a matrix
obtained from matrix
we denote a determinant of a matrix
obtained from matrix ![]() by
replacing its first column by the vector
by
replacing its first column by the vector ![]() ,
meaning
,
meaning
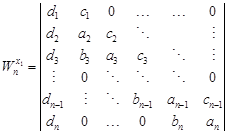 | (5) |
In order to calculate
determinant ![]() we apply the Laplace expansion with
respect to the last column. Hence
we apply the Laplace expansion with
respect to the last column. Hence
| (6) |
where
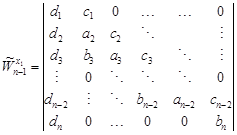 |
For the above determinant we apply the Laplace expansion with respect to the last column and we get
| (7) |
where
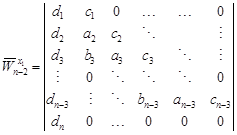 |
Let us observe that
using the Laplace expansion with respect to the last row of
determinant ![]() we obtain
we obtain
| (8) |
Bearing in mind relations (6), (7) and (8), we obtain a second order nonhomogeneous linear recurrence equation of the form
| (9) |
Let us observe that
| (10) |
Hence, in order to
obtain determinant ![]() we
must take into account the recurrence equation (9) together with initial
conditions (10).
we
must take into account the recurrence equation (9) together with initial
conditions (10).
Now, we focus on
the algebraic linear system of equations (2). Firstly, we calculate unknown ![]() . For this purpose we
use the Cramer formulae
. For this purpose we
use the Cramer formulae
| (11) |
At the same time from
first equation of system (2) we get unknown ![]()
| (12) |
Let us observe that from k-th, k = 3,…,n, equation of system (2) we have
| (13) |
Hence we get to the second order nonhomogeneous linear recurrence equation for
unknown ![]() .
.
Thusly, the solution to the algebraic system of equations (2) comes down to resolving the linear recurrence equation (13) with initial conditions (11) and (12).
Remark 1.
If the main matrix of
system (2) has the Toeplitz structure, i.e. ![]() , then the recurrence equation (13) has constant coefficients, so we
can obtain the explicit solution to the system of equations (2).
, then the recurrence equation (13) has constant coefficients, so we
can obtain the explicit solution to the system of equations (2).
3. Special case
In this section we consider a linear algebraic system, which is a
special case of (2) under the assumption that ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . So,
we consider the system of the form
. So,
we consider the system of the form
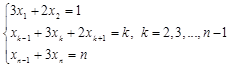 | (14) |
Let us observe that the main matrix of system (14) has the form
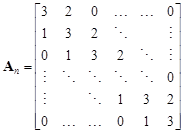 | (15) |
| From (4) we have the recurrence equation for determinant of matrix | (15) |
| (16) |
| and initial conditions |
| (17) |
Following [5], we conclude that the particular solution of recurrence equation (16) satisfying the initial conditions (17) has the form
| (18) |
Now, we are to
calculate the determinant ![]() of the matrix obtained from matrix (15) by
replacing its first column by the vector of constant terms of equations (14).
Bearing in mind (9), we have second
order nonhomogeneous linear recurrence equation for
of the matrix obtained from matrix (15) by
replacing its first column by the vector of constant terms of equations (14).
Bearing in mind (9), we have second
order nonhomogeneous linear recurrence equation for ![]()
| (19) |
At the same time from (10) we have the initial conditions for equation (19)
| (20) |
In order to solve nonhomogeneous linear recurrence equation (19) with initial conditions (20), the method of variation of parameters can be applied [5]. As a result we obtain
| (21) |
| Substituting (20) and (21) into (11), we get |
| (22) |
| Now, from the first equation of the system
(14) we calculate the unknown |
| (23) |
Bearing in mind k-th, k = 3,…,n, equation of system (14) we obtain
| (24) |
Hence, in order to obtain the solution to the algebraic system of equations (14) we have to solve the nonhomogeneous linear recurrence equation (24) with initial conditions (22) and (23). After applying the method of variation of parameters, [5], we obtain
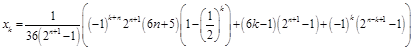 | (25) |
where
![]() .
.
4. Conclusions
It was shown that the solution to the tridiagonal linear system of algebraic equations can be represented by a corresponding second order inhomogeneous linear recurrence equation. The general results were illustrated on the example of a special system in which the main matrix has the Toeplitz tridiagonal structure. As a result, the closed form of solution was obtained.
References
[1] Mazilu I., Mazilu D.A., Williams H.T., Applications of tridiagonal matrices in non-equilibrium statistical physics, Electronic Journal of Linear Algebra 2012, 24, 7-17.
[2] Soujanya G.B.S.L., Reddy Y.N., Computational method for singularly perturbed delay differential equations with layer or oscillatory behaviour, Applied Mathematics and Information Sciences 2016, 10(2), 527-536.
[3] El-Mikkawy M., Atlan F., Algorithms for solving linear systems of equations of tridiagonal type via transformations, Applied Mathematics 2014, 5, 413-422.
[4] Borowska J., Łacińska L., Rychlewska J., Application of difference equation to certain tridiagonal matrices, Scientific Research of the Institute of Mathematics and Computer Science 2012, 3(11), 15-20.
[5] Elaydi S., An Introduction to Difference Equations, Springer, 2005.

