A second example of non-Keller mapping



A SECOND EXAMPLE OF NON-KELLER MAPPING

Sylwia Lara-Dziembek ¹, Grzegorz Biernat ¹, Edyta Pawlak ¹ Magdalena Woźniakowska ²

¹ Institute of Mathematics, Czestochowa University of Technology
Częstochowa, Poland
² Faculty of Mathematics and Computer Science, University of Lodz
Łódź, Poland
sylwia.lara@im.pcz.pl, grzegorz.biernat@im.pcz.pl, edyta.pawlak@im.pcz.pl magdalena_wozniakowska@wp.pl

Abstract. In the article the next nontrivial example of non-Keller mapping having two zeros at infinity is analyzed. The rare mapping of two complex variables having two zeros at infinity is considered. In the article it has been proved that if the Jacobian of the considered mapping is constant, then it is zero.

Keywords: Jacobian, zeros at infinity, rare mappings, Keller mapping

1. Introduction

In this article we analyze the rare polynomial mappings of two complex variables. We consider the mappings having two zeros at infinity [1-3]. It has been shown that if the Jacobian of such mappings is constant, it must be zero. The work is related to the Keller mapping [4-6] (the Keller mapping is a polynomial mapping with the condition ). In the presented paper, the non-Keller mappings are those for which the Jacobian, if it is constant, is zero.

2. The rare mappings

Let are the complex polynomials of degrees , consequently, and having two zeros at infinity. Assume

(1)

and

(2)

where and are the forms of the indicated degrees. These mappings are called rare. Suppose

(3)

Let’s prove that .

3. Basic lemma

Let us provide the following property [7]:

Property. If , then .

Lemma. With the given assumptions we have .

Proof.

Let

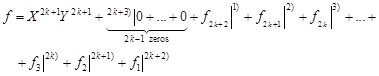(4)

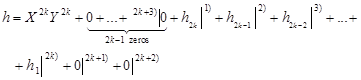(5)

Since the Jacobian is constant, we have consecutively

(6)

so

(7)

and next

(8)

so

(9)

and

(10)

then

(11)

etc.

In the 2k-step we have

(12)

so

(13)

In the next step we obtain

(14)

where

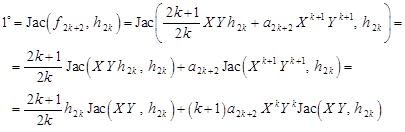(15)

and taking into account the formula (14), we have

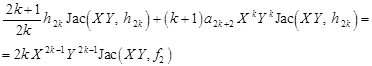(16)

so

(17)

Thus divides (see Property), therefore

,

(18)

and

(19)

In 2k + 2-step we get

(20)

Returning to the formulas (18) and (9), we have

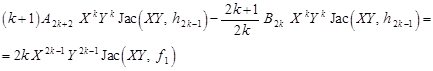(21)

hence

(22)

and so

(23)

where

(24)

Therefore , thus

, (25)

and

,

(26)

In the next step we obtain

(27)

where

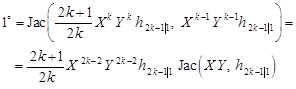(28)

Back to formula (27) we get

(29)

Therefore

(30)

and recalling formula (11) we receive

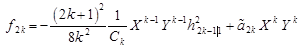(31)

In the following steps to reduce the power of variables (one with every step). The odd steps are an even power, and even steps are the odd power of the mono­mial . In the step (3k + 2), the largest power appears, namely . Then, and this means that . Hence (equation (26)), so . Which completes the proof of the lemma.

4. Conclusion

In the considered example, the form was essential. If we considered the case

(32)

and

(33)

where 2k – 2 appears, then difficult and more interesting considerations show that the above case depends on the form . In this paper, the presented case of rare mapping is therefore a “frontier” case, which is rare and non-Keller mapping having two zeros at infinity. Some remarks on the general case

(34)

and

(35)

will be presented in the later articles.

References

[1] Griffiths P., Harris J., Principles of Algebraic Geometry, New York 1978.

[2] Mumford D., Algebraic Geometry I: Complex Projective Varieties, Springer-Verlag, New York 1975.

[3] Shafarevich I.R., Basic Algebraic Geometry, Springer-Verlag, Berlin, New York 1974.

[4] Wright D., On the Jacobian conjecture, Illinois J. Math. 1981, 25, 3, 423-440.

[5] Van den Essen A., Polynomial Automorphisms and the Jacobian Conjecture, Progress in Mathematics 190, Birkhäuser Verlag, Basel 2000.

[6] Bass H., Connell E.H., Wright D., The Jacobian conjecture: reduction of degree and formal expansion of the inverse, American Mathematical Society. Bulletin, New Series 1982, 7(2), 287-330.

[7] Pawlak E., Lara-Dziembek S., Biernat G., Woźniakowska M., An example of non-Keller mapping, Journal of Applied Mathematics and Computational Mechanics 2016, 15(1), 115-121.