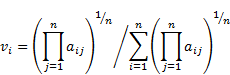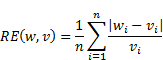Relationship between priority ratios disturbances and priority estimation errors
Tomasz Starczewski
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
RELATIONSHIP BETWEEN PRIORITY RATIOS DISTURBANCES AND PRIORITY ESTIMATION ERRORS
Tomasz Starczewski
Institute of Mathematics, Czestochowa
University of Technology
Częstochowa, Poland
starczewski.t@gmail.com
Abstract. This article is devoted to some problems connected with multicriteria decision analysis. We consider the relationship between the pairwise comparison matrix (PCM) and a priority vector (PV) obtained on the basis of this matrix. The PCM elements are the the decision makers’ judgments about priority ratios i.e. the ratios of weights contained in the PV. It is known, that in the case of consistent matrix, we can obtain the exact value of related PV. However, the real-world practice shows that the decision maker does not create a perfectly consistent PCM, and thus usually in such a matrix the judgment’s errors occur. In our paper we use Monte Carlo simulation to study the relationship between various possible distributions of these errors and the distributions of the errors in estimates of the true PV. In these simulation we apply some initial families distribution and some different parameters. We obtain interesting results which show very slight influence families distribution on final PV errors. Our paper show that much bigger influence on simulation result have adopted parameters than selection distribution family.
Keywords: pairwise comparison matrix, priority vector, inconsistency, randomly generated matrix, decision maker's judgments, analytic hierarchy process
1. Introduction
In multicriteria decision analysis (MDA), the aim is to rank a finite number of alternatives with respect to a finite number of attributes (criteria), i.e. to find a priority vector (PV) that elements reflect, how much each alternative is desired with respect to a given attribute and then to develop an overall ranking with respect to all attributes. In the analytic hierarchy process (AHP) the decision maker (DM) compares alternatives (each one to all the others) with respect to a particular attribute and puts their judgements about all priority ratios into the pairwise comparison matrix (PCM). This approach is justified by psychology, which says that our brain gives the most exact judgments when we compare only two stimuli at once. When we compare only two stimuli and we consider only one criterion, we can quite precisely tell how many times one is better (or worse) than the other. The number is called a priority ratio [1].
When we compare two objects we usually describe our judgment about the relative preference with an adverb. When we create a PCM, we need to know numbers which indicate how many times one alternative is better than any other. So, Thomas Saaty has proposed a scale, which we can use to translate comparing words (adverbs) to numbers [1]. Despite its usefulness, its disadvantage is that it cuts down the set of possible ratios to 8 numbers. It is clear that sometimes we need more than 8 ratios, so rounding to Saaty’s scale will cause, in this case, unavoidable errors in our PCM (e.g. [2-5]).
When we have a given PCM, we must obtain the PV in order to get information about DM's priorities. There are a lot of PCM-based PV estimation methods allowing us to extract the PV from the PCM [6-12]. All the methods work well when the PCM is consistent [1, 2, 6, 8, 9, 13]. However the real-world practice shows that DM-s judgments are usually inconsistent [1, 2, 6, 8]. There is a number of inconsistency indices whose task is the “measuring” of inconsistency of the PCM [8, 9, 14-16]. In practice, many users use this indices to evaluation correctness their researches. For this purpose they assumed the suggested by Saaty or other authors level of the indices value [1, 13]. However, it is still not known whether the smaller value of a given index is related to smaller value of PV estimation errors. We do not know what is the relationship between priority ratios disturbances in the PCM and errors in the PV obtained from this PCM. This relationship is important because practitioners often try to improve the PCM gained from judgments in questionnaires but they can’t be sure that they improve final PV. So, in our paper, we try observe this relationship.
2. The prioritization problem - formal preliminaries
Formally, the
PV is an n-dimensional vector ![]() with components
with components ![]() , describing the degree of fulfillment of an attribute or all
attributes with particular alternatives.
, describing the degree of fulfillment of an attribute or all
attributes with particular alternatives.
Definition 1
The Pairwise comparison matrix ![]() is a matrix with the elements
is a matrix with the elements ![]() that are interpreted as DM judgments about priority ratios
that are interpreted as DM judgments about priority ratios ![]() .
.
Definition 2
A given matrix ![]() is called a reciprocal PCM if the condition
is called a reciprocal PCM if the condition
| (1) |
holds for any i, j = 1,2,…,n.
Definition 3
A given matrix ![]() is called a consistent PCM
(or cardinally transitive) if it is reciprocal and its elements
satisfy the condition:
is called a consistent PCM
(or cardinally transitive) if it is reciprocal and its elements
satisfy the condition:
| (2) |
for all i, j, k = 1,2,…,n.
Theorem 1
The necessary and sufficient condition for
any positive matrix ![]() to be consistent PCM is the
existence of a certain vector
to be consistent PCM is the
existence of a certain vector ![]() satisfying
satisfying
|
|
|
for all i, j = 1,2,…,n.
Therefore in the ideal case, when the DM creates a consistent PCM, the following equation holds:
| (4) |
This means that in a consistent case the PV
is the eigenvector of the PCM
corresponding to eigenvalue n, which is
the principal eigenvalue of PCM, i.e.,
the largest solution of the characteristic equation:![]() .
.
However, as we mentioned earlier, consistent case rarely occurs. If the PCM is not consistent we assume that priority ratios can be expressed by the following stochastic model [3, 6, 8, 17-19]:
|
|
|
Probability distributions of the so-called perturbation
factor ![]() (PF) mainly involve gamma, log-normal, uniform (e.g.
[8, 11, 12, 17, 18]) and truncated normal (e.g.
[6, 19, 20]). In our study, we also consider
the four most popular ones.
(PF) mainly involve gamma, log-normal, uniform (e.g.
[8, 11, 12, 17, 18]) and truncated normal (e.g.
[6, 19, 20]). In our study, we also consider
the four most popular ones.
According to Theorem 1, in the inconsistent case we cannot find PV which would satisfy equation (4). In such a case, Saaty proposed using the normalized right eigenvector associated with the largest eigenvalue as an estimate of the true PV [1-3]. Therefore, to obtain the PV estimate (PVE), we need to solve the general eigenvector equation:
| (6) |
where: ![]() -
principal eigenvalue of PCM,
-
principal eigenvalue of PCM, ![]() - eigenvector connected to
- eigenvector connected to ![]() .
.
However it is not the only method used to obtain PVE. Another popular one recommended by Crawford & Williams [17, 21-23], is the geometric mean procedure (GM). To calculate elements of the PV within this method we use the following formula:
|
|
This is a very simple method and in AHP practice it is applied almost as frequently as REV and that is why we use it in our simulations.
If we assume in our model that elements of the PCM satisfy condition (5) with a certain p.d. of PF, it is clear that the PVE (obtained by any method) will contain errors. Such errors can be defined (measured) in various ways. However it is argued, see [8, 9], that in the context of AHP, the so-called mean relative error is much more important than the others. This is defined by following:
|
|
where: ![]() - elements of initial PV,
- elements of initial PV, ![]() - elements of PVE obtained from disturbed PCM. In our paper we use
this definition for the estimation errors.
- elements of PVE obtained from disturbed PCM. In our paper we use
this definition for the estimation errors.
3. Simulation frameworks
We have mentioned that in practice it is not possible to get such DM judgments that create a consistent PCM. We have also said it is obvious that disturbances in PCM result finally in PVE errors. It seems to be the truth but here another question is arising: What is the influence of disturbances in the PCM on errors in the PVE? Are disturbances in the PCM proportional to final errors in the PVE? What is the relationship between the probability distribution of the PF and the distribution of errors in the PVE? In order to answer these questions, we perform Monte Carlo experiments (see e.g. [6, 8]).
In our simulations, we consider three
different dimensions of PV, ![]() and 12 different probability distributions of the PF (denoted
as
and 12 different probability distributions of the PF (denoted
as ![]() ) belonging to the one of 4 distribution families. The simulation
experiments consist of the following steps:
) belonging to the one of 4 distribution families. The simulation
experiments consist of the following steps:
1. Randomly
generate elements of a PV: ![]() and make the related perfect PCM based
on formula (3).
and make the related perfect PCM based
on formula (3).
2. For
each element in the upper triangle of the PCM, randomly generate value ![]() according to chosen
according to chosen ![]() and replace element
and replace element ![]() by
by ![]() .
.
3. Replace elements in the lower triangle of the PCM with the reciprocities of appropriate elements from the created upper triangle.
4. After
all replacements use the GM to calculate the PVE: ![]() .
.
5. Calculate relative
error in PVE in comparing with the initial PV, i.e. ![]() .
.
6. Repeat steps 1 –
5: ![]() times for
times for ![]() - dimension PV (16, 25 or 36 times respectively for
- dimension PV (16, 25 or 36 times respectively for ![]() ).
).
7. Repeat steps 1 – 6: 300 times.
8. Return value of
errors ![]() assigned to
appropriate
assigned to
appropriate ![]() and
and ![]() and save it
in database.
and save it
in database.
In our simulation we use 4 of the most recommended probability distribution families in literature, i.e. gamma, log-normal, truncated normal and uniform, [6, 8, 11, 18-20]. In each case the distribution parameters are arranged so that the PF possesses the following features [3, 5, 18]:
1. Expected
value of ![]() equals 1.
equals 1.
2. Standard deviation
of ![]() is equal to
is equal to ![]() being given positive constant
being given positive constant ![]() (in our experiments
(in our experiments ![]() = 0.1, 0.2 or 0.3).
= 0.1, 0.2 or 0.3).
To satisfy the above requirements, we adopt the following parameters for the particular distribution families:
·
![]()
o
gamma: ![]()
o
log-normal: ![]()
o
truncated normal:![]()
o
uniform: ![]()
·
![]()
o
gamma: ![]()
o
log-normal: ![]()
o
truncated normal: ![]()
o
uniform: ![]()
·
![]()
o
gamma: ![]()
o
log-normal:![]()
o
truncated normal: ![]()
o
uniform: ![]()
4. Results
Under the described above framework, we have obtained a database of relative errors in the PVE. These errors gained in a random sample are realizations of certain random variables which have their own probability distributions. We do not know what their distributions are in the analytic meaning, but we know the realization of these distributions. Thus when we analyse the gained database, we get information about estimate parameters and approximate probability distributions of real ones.
Our database contains subsets of 4800, 7500 or 10800 outcomes respectively for PV dimensions: 4, 5 or 6. In order to compare relative errors in the PVE obtained for a different distribution of PCM disturbances, we have calculated some parameters of these errors distributions. For each distribution of the PF, we calculate the following sample parameters: minimum and maximum value, mean, standard deviation and quantile of rank: 0.05, 0.1, 0.5, 0.9, 0.95. We have collected values of parameters in tables (Tables 1-5 in the Appendix A). In these tables, we have collected results describing the PVE error distributions, gained for chosen dimensions of the PV and chosen standard deviations of the PF probability distributions. In each table, results are collected for each considered distribution family. The presented tables show us the following interesting findings:
1. The means and all rank quantiles in most cases have similar values.
2. Maximum and minimum values and standard deviations are different but do not manifest any dependence on the shape of the initial distribution.
3. None of the initial distributions generate parameters which are tendentiously bigger or smaller than parameters gained for other initial distributions.
4. The means, all rank quantiles and minimum values increase when the standard deviation of the initial distribution increases.
5. All rank quantiles in most cases increase when the dimension of the PV increases.
For a better illustration of the similarities and differences of the
obtained
experimental distributions of PVE errors,
we also present histograms (Appendix B). The histograms of the values of
the PF are compared with the histograms of resulting estimation errors in the
PVE. Thus we have 36 histograms, but we present
only 6 of them, namely these obtained for ![]() and a chosen standard deviation for different families (Figures
1-6). Other histograms present similar dependence, so they are omitted here.
When we look at these figures, we can notice that PVE
errors histograms’ shapes in all cases are rather similar, in contrast to histograms of the input PCM disturbances.
Obviously, here one can observe the same distribution features that we can
notice when we analyse parameters presented in Tables 1-5. Histograms change
when the standard deviation increases, but in the same way as
it is reflected by the parameters. The shape of the histograms of PVE errors
does not change significantly when we consider a different standard deviation
or various PV dimensions. Greater values of these parameters affect only the
size of the histograms, not their shapes. The size is bigger and reflects the
fact that bigger errors occur more frequently.
and a chosen standard deviation for different families (Figures
1-6). Other histograms present similar dependence, so they are omitted here.
When we look at these figures, we can notice that PVE
errors histograms’ shapes in all cases are rather similar, in contrast to histograms of the input PCM disturbances.
Obviously, here one can observe the same distribution features that we can
notice when we analyse parameters presented in Tables 1-5. Histograms change
when the standard deviation increases, but in the same way as
it is reflected by the parameters. The shape of the histograms of PVE errors
does not change significantly when we consider a different standard deviation
or various PV dimensions. Greater values of these parameters affect only the
size of the histograms, not their shapes. The size is bigger and reflects the
fact that bigger errors occur more frequently.
All histograms we received in our studies demonstrate similar features. We observe that independently of considered distribution family of the PF, when the standard deviation of a distribution increases, the histograms also show greater support of the PV errors’ distribution.
5. Conclusions
The results of the Monte Carlo simulation presented in this paper involve research for some cases of PF’s distributions and size of PV. However, our experiment shows visibly some dependencies between priority ratio disturbances in the PCM and priority estimation errors in the final PV. Moreover, we have observed these dependences practically irrespective of the considered disturbance distribution so one can expect the same dependences in case of other distributions. We have also considered several variants of the same distribution family and we have experienced the same. Although we do not consider all cases of the standard deviation, the dependences in the ones shown are clear. This observation are corresponding to research findings obtained by other authors that have made researches with using Monte Carlo simulation for example to Kazibudzki [9] because their results does not demonstrate dependence of chosen PF distribution.
However one of the most interesting result for us was the observed shape of experimental distributions of errors in the PVE because it was very close for completely different PCM disturbance distributions. It probably means that for all initial disturbance distributions we will observe the same shape of the probability distribution of final errors in PVE. It is a significant conclusion because it means the choice of the initial distribution’s family is not as important as the choice of the initial distribution’s parameters. This result makes any discussions on family’s disturbance distributions useless [11, 12, 17, 18]. Of course for ensuring reality of experiments we can use different distribution families or mix them together but it probably does not have influence on results.
When we studied the obtained experiment distributions, we observed quite big differences between maximum values and standard deviations and sometimes occurring irregular differences between other parameters. Considering this, we found that influence on our results would also have the initial PV. Notice that when we compare two completely different values of PV’s elements (from [0,1]), we get big priority ratios in the PCM. These priority ratios are unlimited in our simulation. Of course in the next step of simulation the priority ratios are rounded to Saaty’s scale but this operation may cause, in this case, big errors in the obtained value of the PVE. Here arise guess that research findings will be different if we apply other scale or no scale is applied. This is interesting research field so we are going to carry out this kind of researches.
The next interesting research field is connected with the question about the meaningfulness of a PCM inconsistency examination. It is known that in AHP practice, one of the routine operations is testing of the so-called inconsistency of the PCM which requires one to calculate the so-called inconsistency index [1, 6, 8, 9, 13-15]. Although various different inconsistency indices are proposed in literature, it is not certain that the more consistent PCM gives less erroneous PVE. Many authors study presented in literature inconsistency indices propriety [8, 14, 15]. We expect that the conclusions presented in this paper will be helpful in the study of the dependence between inconsistency of the PCM and the resulting PV’s correctness. For such simulations it is important to know what the influence of disturbance in PCM on PV errors is, and it results from experiments discussed here, that the shape of the PF distribution has rather marginal importance.
References
[1] Saaty T.L., Decision making - the analytic hierarchy and network processes (Ahp/Anp), Journal of Systems Science and Systems Engineering 2004, 13, 1.
[2] Saaty T.L., The Analytic Hierarchy Process, McGraw Hill, New York 1980.
[3] Saaty T.L., Decision making with the AHP: Why is the principal eigenvector necessary, European Journal of Operational Research, 145, 85-91, 2003.
[4] Sun L., Greenberg B.S., Multiple group decision making: optimal priority synthesis from pairwise comparisons, Journal of Optimization Theory and Applications 2006, 130(2), 317-338.
[5] Ishizaka A., Labib A., Review of the main developments in the analytic hierarchy process, Expert Systems with Applications 2011, 38(11), 14336-14345.
[6] Grzybowski A.Z., Note on a new optimization based approach for estimating priority weights and related consistency index, Expert Systems with Applications 2012, 39, 11699-11708.
[7] Bryson N., A goal programming method for generating priority vectors, Journal of the Operational Research Society 1995, 46, 641-648.
[8] Grzybowski A.Z., New results on inconsistency indices and their relationship with the quality of priority vector estimation, Expert Systems with Applications 2016, 43, 197-212.
[9] Kazibudzki P.T., An examination of performance relations among selected consistency measures for simulated pairwise judgments, Annals of Operations Research 2016, 236/2, 1-20.
[10] Lin C.-C., An enhanced goal programming method for generating priority vectors, Journal of the Operational Research Society 2006, 57, 1491-1496.
[11] Choo E.U., Wedley W.C., A common framework for deriving preference values from pairwise comparison matrices, Computer & Operations Research 2004, 31, 893-908.
[12] Basak I., Comparison of statistical procedures in analytic hierarchy process using a ranking test, Mathematical and Computer Modelling 1998, 28, 105-118.
[13] Wrzalik A., Niedbał R., Sokołowski A., The model of managerial decisions’ support in the process of choosing an internet shop application, Polish Journal of Management Studies 2015, 12(2), 2081-7452.
[14] Kazibudzki P.T., Redefinition of triad's inconsistency and its impact on the consistency measurement of pairwise comparison matrix, Journal of Applied Mathematics and Computational Mechanics 2016, 15(1), 71-78, DOI:10.17512/jamcm.2016.1.07.
[15] Brunelli M., Fedrizzi M., Axiomatic properties of inconsistency indices for pairwise comparisons, Journal of the Operational Research Society, Published online 04 December 2013.
[16] Altuzarra A., Moreno-Jiménez J.M., Salvador M., Consensus building in AHP-group decision making: A Bayesian approach, Operations Research 2010, 1755-1773.
[17] Budescu D.V., Zwick R., Rapoport A., Comparison of the analytic hierarchy process and the geometric mean procedure for ratio scaling, Applied Psychological Measurement 1986, 10, 69-78.
[18] Zahedi F., A simulation study of estimation methods in the analytic hierarchy process, Socio-Economic Planning Sciences 1986, 20, 347-354.
[19] Lin C.-C., A revised framework for deriving preference values from pairwaise comparison matrices, Europpean Journal of Operational Research 2007, 176, 1145-1150.
[20] Dijkstra T.K., On the extraction of weights from pairwaise comparison matrices, Central European Journal of Operations Research 2013, 21, 103-123.
[21] Crawford G., Williams C.A., A note on the analysis of subjective judgment matrices, Journal of Mathematical Psychology 1985, 29, 387-405.
[22] Cook W.D., Kress M., Deriving weights from pairwise comparison ratio matrices: An axiomatic approach, European Journal of Operational Research 1988, 37, 355-362.
[23] Saaty T.L., Hu G., Ranking by eigenvector versus other methods in the Analytic Hierarchy Process, Applied Mathematical Letters 1998, 11(4), 121-125.
Appendix A
Table 1
Parameters of experimental probability distributions of RE in relation to different distributions of eij . Input parameters: s = 0.1, n = 5, sample size: 7500
|
Distributions of Priority Disturbance |
Min |
Max |
Mean |
SD |
0.05-quant |
0.1-quant |
ME |
0.9-quant |
0.95-quant |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 2
Parameters of experimental probability distributions of RE in relation to different distributions of eij . Input parameters: s = 0.2, n = 5, sample size: 7500
|
Distributions of Priority Disturbance |
Min |
Max |
Mean |
SD |
0.05-quant |
0.1-quant |
ME |
0.9-quant |
0.95-quant |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 3
Parameters of experimental probability distributions of RE in relation to different distributions of eij . Input parameters: s = 0.3, n = 5, sample size: 7500
|
Distributions of Priority Disturbance |
Min |
Max |
Mean |
SD |
0.05-quant |
0.1-quant |
ME |
0.9-quant |
0.95-quant |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 4
Parameters of experimental probability distributions of RE in relation to different distributions of eij . Input parameters: s = 0.2, n = 4, sample size: 4800
|
Distributions of Priority Disturbance |
Min |
Max |
Mean |
SD |
0.05-quant |
0.1-quant |
ME |
0.9-quant |
0.95-quant |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 5
Parameters of experimental probability distributions of RE in relation to different distributions of eij . Input parameters: s = 0.2, n = 6, sample size: 10800
|
Distributions of Priority Disturbance |
Min |
Max |
Mean |
SD |
0.05-quant |
0.1-quant |
ME |
0.9-quant |
0.95-quant |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Appendix B
Appendix B
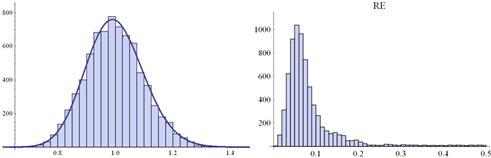
![]() Fig.
1. Histogram of a random sample of eij distributed according
Fig.
1. Histogram of a random sample of eij distributed according ![]() .
Size of the sample: 7500 (left-hand side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
.
Size of the sample: 7500 (left-hand side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
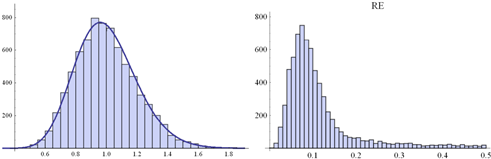
![]() Fig.
2. Histogram of a random sample of eij distributed according
Fig.
2. Histogram of a random sample of eij distributed according ![]() .
Size of the sample: 7500 (left-hand side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
.
Size of the sample: 7500 (left-hand side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
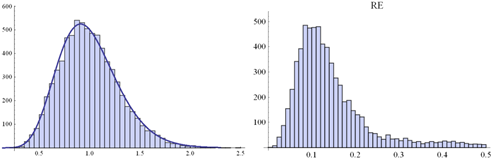
Fig. 3. Histogram of a random sample of eij distributed
according ![]() .
Size of the sample: 7500 (left-hand side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
.
Size of the sample: 7500 (left-hand side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
![]()
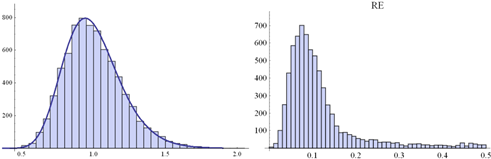
![]() Fig.
4. Histogram of a random sample of eij distributed according
Fig.
4. Histogram of a random sample of eij distributed according ![]() . Size of the sample: 7500 (left-hand
side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
. Size of the sample: 7500 (left-hand
side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
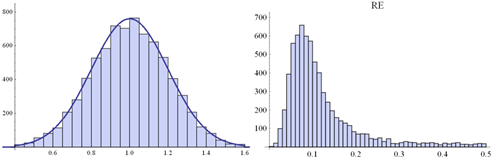
![]() Fig.
5. Histogram of a random sample of eij distributed according
Fig.
5. Histogram of a random sample of eij distributed according ![]() . Size of the sample: 7500 (left-hand side) along the
histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
. Size of the sample: 7500 (left-hand side) along the
histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
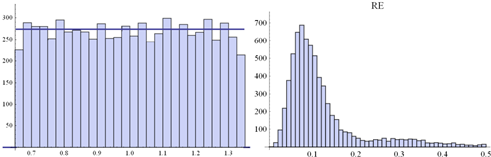
Fig. 6. Histogram of a random sample of eij distributed
according ![]() .
Size of the sample: 7500 (left-hand side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)
.
Size of the sample: 7500 (left-hand side) along the histogram of RE-s
obtained from 7500 PCMs (5x5) disrupt by these eij’s (right-hand side)