On the convergence of multicomplex M-J sets to the Steinmetz hypersolids
Andrzej Katunin
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
ON THE CONVERGENCE OF MULTICOMPLEX M-J SETS TO THE STEINMETZ HYPERSOLIDS
Andrzej Katunin
Institute of Fundamentals of Machinery
Design, Silesian University of Technology
Gliwice, Poland
andrzej.katunin@polsl.pl
Abstract. In this paper, the analysis of generalized multicomplex Mandelbrot-Julia (henceforth abbrev. M-J) sets is performed in terms of their shape when a degree of an iterated polynomial tends to infinity. Since the multicomplex algebras result from a tensor product of complex algebras, the dynamics of multicomplex systems described by iterated polynomials is different with respect to their complex and hypercomplex analogues. When the degree of an iterated polynomial tends to infinity the M-J sets tend to the higher dimensional generalization of the Steinmetz solid, depending on the dimension of a vector space, where a given generalization of M-J sets is constructed. The paper describes a case of bicomplex M-J sets with appropriate visualizations as well as a tricomplex one, and the most general case - the muticomplex M-J sets, and their corresponding geometrical convergents.
Keywords: generalized M-J sets, multicomplex M-J sets, convergence, Steinmetz hypersolid
1. Introduction
The Mandelbrot set and corresponding Julia sets were intensively studied during the 80s of the XX century and many fascinating properties of these sets were observed to date. Considering that M-J sets are defined on a complex plane C in the form of a quadratic polynomial:
| (1) |
nothing stands in a way of generalization of these sets both in terms of degree of the polynomial as well as in terms of a vector space in which it is constructed. The first generalization of complex M-J sets to quaternionic H ones was defined by Holbrook [1], and then further developed and analysed by several authors [2-6]. Then, Wang and Sun [7] proposed a generalization of quaternionic M-J sets in terms of a degree of an iterated polynomial p:
| (2) |
However, these studies show that the dynamics of quaternionic maps is trivial with respect to their complex analogues. The same can be observed for the further generalization - the M-J sets in octonions O, introduced and studied by Griffin and Joshi in the early 90s of the XX century [8-10].
An alternative to the above-mentioned generalization was proposed by Rochon and his team. In 2000, Rochon introduced a generalization of M-J sets to a bicomplex vector space [11], further several studies on properties of this type of M-J sets [12-14] as well as their generalization to tricomplex [15] and multicomplex [16] analogues were proposed. The generalized version of bicomplex M-J sets with respect to a degree of an iterated polynomial was also studied by Zireh [17], and Wang and Song [18]. The performed studies of the above-mentioned teams show, in general, the different dynamics with respect to hypercomplex M-J sets which reflect, in particular, in varying character of changing a shape of these sets for varying values of a constant c in an iterated polynomial of type (2).
In the following study, the convergents of
the multicomplex M-J sets, i.e. the sets for ![]() , are analysed. The study starts with
the simplest case - the bicom-
plex M-J sets, through the tricomplex ones, and ends with the most general case
n-complex or multicomplex M-J sets. In each of the considered cases it
was shown that the shapes of the convergents of M-J sets in multicomplex vector
spaces tend to higher-dimensional generalizations of a Steinmetz solid.
, are analysed. The study starts with
the simplest case - the bicom-
plex M-J sets, through the tricomplex ones, and ends with the most general case
n-complex or multicomplex M-J sets. In each of the considered cases it
was shown that the shapes of the convergents of M-J sets in multicomplex vector
spaces tend to higher-dimensional generalizations of a Steinmetz solid.
2. Preliminaries to multicomplex algebras
Let us begin with the preliminaries of
multicomplex vector spaces from the sim-
plest case - a 4-algebra of bicomplex numbers ![]() . For simplicity, the following notation
is introduced: C2,
where the lower index denotes a number of tensor product operations on complex
algebras (thus C2 denotes
an algebra of bicomplex numbers, C3 denotes an algebra of tricomplex numbers, etc.). The
bicomplex
numbers can be expressed in the symbolic representation as follows:
. For simplicity, the following notation
is introduced: C2,
where the lower index denotes a number of tensor product operations on complex
algebras (thus C2 denotes
an algebra of bicomplex numbers, C3 denotes an algebra of tricomplex numbers, etc.). The
bicomplex
numbers can be expressed in the symbolic representation as follows:
| (3) |
where ![]() are the associators,
are the associators, ![]() ,
, ![]() and
and ![]() are the imaginary units with the
following interrelations:
are the imaginary units with the
following interrelations: ![]() ,
, ![]() ,
, ![]() .
Since C2 is
commutative and considering the existence of idempotents for C2 (which follows from the
definition of bicomplex numbers):
.
Since C2 is
commutative and considering the existence of idempotents for C2 (which follows from the
definition of bicomplex numbers):
| (4) |
where ![]() (or just C
since C ≡ C1),
(or just C
since C ≡ C1),
![]() and
and ![]() are
idempotents which means that during multiplication
are
idempotents which means that during multiplication ![]() and
and ![]() do not change the initial
result:
do not change the initial
result: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . C2 is closed under addition and
multiplication operations (which are necessary to perform
an iteration of a polynomial of type (2)), and these operations can be
performed element-wise. Considering that
. C2 is closed under addition and
multiplication operations (which are necessary to perform
an iteration of a polynomial of type (2)), and these operations can be
performed element-wise. Considering that ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
the addition and multiplication is defined as follows:
,
the addition and multiplication is defined as follows:
| (5) |
| (6) |
The next generalization of C2 is an 8-algebra of tricomplex numbers C3 with the following symbolic representation [15]:
| (7) |
with the
following interrelations between imaginary units: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Similarly to C2, the tri-complex numbers can be
presented as a pair of bicomplex elements:
. Similarly to C2, the tri-complex numbers can be
presented as a pair of bicomplex elements:
| (8) |
where ![]() and
and ![]() are idempotents,
or in a form of a quadruple of complex elements:
are idempotents,
or in a form of a quadruple of complex elements:
| (9) |
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
the addition and multiplication of two tricomplex
numbers
,
the addition and multiplication of two tricomplex
numbers ![]() and
and ![]() can
be performed element-wise:
can
be performed element-wise:
| (10) |
| (11) |
The above expressions can be generalized to a hypercomplex number space Cn, which is n-tensor product 2n-algebra with a following symbolic representation [19]:
| (12) |
where ![]() , or
alternatively:
, or
alternatively:
| (13) |
where ![]() ,
, ![]() . Thus, every multicomplex number in Cn contains 2n elements with the
associators defined in R, or equivalently 2n–m
elements defined in Cm for
. Thus, every multicomplex number in Cn contains 2n elements with the
associators defined in R, or equivalently 2n–m
elements defined in Cm for
![]() .
.
The multicomplex algebra is commutative and idempotent representation of multicomplex number has the form [16]:
| (14) |
where ![]() and
and ![]() are
idempotents. Extending (5)-(6) and (10)-(11) to the case of Cn the addition and
multiplication operations of two multi-complex numbers
are
idempotents. Extending (5)-(6) and (10)-(11) to the case of Cn the addition and
multiplication operations of two multi-complex numbers ![]() and
and ![]() can be performed element-wise
as:
can be performed element-wise
as:
| (15) |
| (16) |
3. Multicomplex M-J sets
Having defined multicomplex algebras and basic operations on multicomplex numbers, one can define M-J sets as follows:
| (17) |
and correspondingly:
| (18) |
The authors of [16] proved that M sets and
filled J sets defined in Cn are
connected and the escaping-time radius (known also as a bailout values) equals
2. Moreover, the connectedness of J sets defined in Cn are of three types: connected, when ![]() , totally disconnected (i.e. homeomorphic
to the Cantor dust) when
, totally disconnected (i.e. homeomorphic
to the Cantor dust) when ![]() and
and ![]() , where
, where ![]() is a strong basin of attraction at
infinity (see details in [16]), and disconnected, but not totally in all
other cases. More
details on connectedness and other properties of M-J sets defined in Cn can be found in [16].
is a strong basin of attraction at
infinity (see details in [16]), and disconnected, but not totally in all
other cases. More
details on connectedness and other properties of M-J sets defined in Cn can be found in [16].
4. Convergence analysis
When changing a degree p of an
iterated polynomial of type (2) significant changes in a shape of the resulting
M-J sets can be observed for the small values
of p. However, when ![]() , a shape of these sets tends to a specific geometrical shape.
An example of such behavior for
, a shape of these sets tends to a specific geometrical shape.
An example of such behavior for ![]() is presented in
Figure 1.
is presented in
Figure 1.



(a) ![]() ; (b)
; (b) ![]() ; (c)
; (c) ![]() ;
;



(d) ![]() ;
(d)
;
(d) ![]() ; (f)
; (f) ![]() ;
;
Fig. 1. 3D projections of bicomplex J sets for c = (–0.5,0.5,0,0) and various values of p
Theorem 1. The
generalized bicomplex M-J sets of type (2) tend to a 4-dimen-sional Steinmetz
solid when ![]() .
.
Before proceeding with the proof of the Theorem 1, it is necessary to define the generalized n-dimensional Steinmetz solid or the Steinmetz hypersolid.
Definition 1. We
say that the Steinmetz hypersolid ![]() is
an n-dimensional solid resulting from an intersection of Q n-cylinders
(Q ≥ 2) of equal radii r denoted as
is
an n-dimensional solid resulting from an intersection of Q n-cylinders
(Q ≥ 2) of equal radii r denoted as ![]() ,
where
,
where ![]() ,
, ![]() is a
q-th coordinate axis and
is a
q-th coordinate axis and ![]() is a unitary basis
in Rn unique for each q, and being their
common:
is a unitary basis
in Rn unique for each q, and being their
common:
| (19) |
Proof. Suppose c = 0
in (2) defined in bicomplex numbers which is equivalent to the case when ![]() . Then (2) takes
a form:
. Then (2) takes
a form:
| (20) |
Recalling representation of a product of two bicomplex numbers by pairs of complex numbers (6), one can present (20) in the following form [20]:
| (21) |
where ![]() , x1,…,4 are the coordinates in C2. Following this, we can
rewrite (20) in the form:
, x1,…,4 are the coordinates in C2. Following this, we can
rewrite (20) in the form:
| (22) |
and
considering that C2 results
from a tensor product ![]() , the
boundary of sets of prisoner points, i.e. the M and “filled” J sets are given
by a common of intersection of two 3-cylinders:
, the
boundary of sets of prisoner points, i.e. the M and “filled” J sets are given
by a common of intersection of two 3-cylinders:
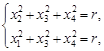 | (23) |
where r
= 1. In the limit case (when ![]() ) the resulting set does not have fractal properties. The system (23) describes
) the resulting set does not have fractal properties. The system (23) describes ![]() .
.
Corollary 1. One
can extend Theorem 1 as follows: The generalized tricomplex M-J sets of type
(2) tend to 8-dimensional Steinmetz solid when ![]() .
.
Proof. Considering Definition 1 and a recursive equation (20) defined in C3, one can express such an equation in terms of quadruple of complex numbers as follows:
| (24) |
By analogy
to the proof of Theorem 1, the tricomplex M-J sets tend to ![]() given
by:
given
by:
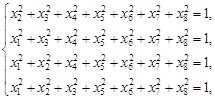 | (25) |
when ![]() .
.
Corollary 2. One
can also extend Theorem 1 to the most general form: The generalized
multicomplex M-J sets of type (2) tend to an n-dimensional Steinmetz
solid when ![]() .
.
Proof.
Considering Definition 1 and a recursive equation (20) defined in Cn one can express such
equation in terms of n/2-tuple of complex numbers. By analogy to the proofs of Theorem 1 and Corollary 1,
the multicomplex M-J sets tend to ![]() given by:
given by:
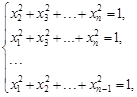 | (26) |
when ![]() .
.
5. Conclusions
In the presented study, the convergents of
multicomplex M-J sets were investigated. Starting from the simplest case - the
bicomplex algebra, it was shown that
in contrast to hypercomplex generalizations of M-J sets [21], the multicomplex ones tend to higher dimensional Steinmetz
solids (with ![]() ) which, in a general case, results from the intersection of n/2
n-cylinders in Cn .
) which, in a general case, results from the intersection of n/2
n-cylinders in Cn .
References
[1] Holbrook J.A.R., Quaternionic Fatou-Julia sets, Ann. Sci. Math. Québec 1987, 11, 79-94.
[2] Norton A.V., Julia sets in the quaternions, Comput. Graph. 1989, 13(2), 267-278.
[3] Gomatam J., Doyle J., Steves B., McFarlane I., Generalization of the Mandelbrot set: quaternionic quadratic maps, Chaos Soliton. Fract. 1995, 5(6), 971-986.
[4] Bedding S., Briggs K., Iteration of quaternion maps, Int. J. Bifurcat. Chaos 1995, 5(3), 877-881.
[5] Petek P., Circles and periodic points in quaternionic Julia sets, Open Syst. Inf. Dyn. 1997, 4(4), 487-492.
[6] Lakner M., Petek P., The one-equator property, Experiment. Math. 1997, 6(2), 109-115.
[7] Wang X.Y., Sun Y.Y., The general quaternionic M-J sets on the mapping z ← zα + c, Comput. Math. Appl. 2007, 53(11), 1718-1732.
[8] Griffin C.J., Joshi G.C., Octonionic Julia sets, Chaos Soliton. Fract. 1992, 2(1), 11-24.
[9] Griffin C.J., Joshi G.C., Transition points in octonionic Julia sets, Chaos Soliton. Fract. 1993, 3(1), 67-88.
[10] Griffin C.J., Joshi G.C., Associators in generalized octonionic maps, Chaos Soliton. Fract. 1993, 3(3), 307-319.
[11] Rochon D., Generalized Mandelbrot set for bicomplex numbers, Fractals 2000, 8(4), 355-368.
[12] Rochon D., On a generalized Fatou-Julia theorem, Fractals 2003, 11(3), 213-219.
[13] Martineau É., Rochon D., On a bicomplex distance estimation for the Tetrabrot, Int. J. Bifurcat. Chaos 2005, 15(9), 3039-3050.
[14] Matteau C., Rochon D., The inverse iteration method for Julia sets in the 3-dimensional space, Chaos Soliton. Fract. 2015, 75, 272-280.
[15] Parisé P.O., Rochon D., A study on dynamics of the tricomplex polynomial ηp + c, Nonlin. Dyn. 2015, 82(1), 157-171.
[16] Garant-Pelletier V., Rochon D., On a generalized Fatou-Julia theorem in multicomplex spaces, Fractals 2009, 17(3), 241-255.
[17] Zireh A., A generalized Mandelbrot set of polynomials of type Ed for bicomplex numbers, Georgian Math. J. 2008, 15(1), 189-194.
[18] Wang X.Y., Song W.J., The generalized M-J sets for bicomplex numbers, Nonlin. Dyn. 2013, 72(1), 17-26.
[19] Price G.B., An Introduction to Multicomplex Spaces and Functions, Marcel Dekker Inc., New York 1991.
[20] Rönn S., Bicomplex algebra and function theory, arXiv: math/0101200v1, 2001, 1-71.
[21] Katunin A., Fedio K., On a visualization of the convergence of the boundary of generalized Mandelbrot set to (n-1)-sphere, J. Appl. Math. Comput. Mech. 2015, 14(1), 63-69.

