L∞-error estimates of finite element methods with Euler time discretization scheme for an evolutionary HJB equations with nonlinear source terms
Salah Boulaaras
,Med Amine Bencheikh Le Hocine
,Mohamed Haiour
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
L∞-ERROR ESTIMATES OF FINITE ELEMENT METHODS WITH EULER TIME DISCRETIZATION SCHEME FOR AN EVOLUTIONARY HJB EQUATIONS WITH NONLINEAR SOURCE TERMS
Salah Boulaaras 1,2, MedAmine Bencheikh Le Hocine 3,4, Mohamed Haiour 3
1 Department
of Mathematics, College of Science and Arts, Ar-Ras, Qassim University
Kingdom Of Saudi Arabia
2 Laboratory of Fundamental and Applied Mathematics of Oran (LMFAO),
University of Oran 1, Ahmed Benbella. Algeria, Tel +966559618327.
3 Department of Mathematics, Faculty of Science, University of
Annaba, Box. 12
Annaba 23000. Algeria
4 Tamanghesset
University Center, Box. 10034, Sersouf, Tamanghesset 11000, Algeria.
S.Boularas@qu.edu.sa or saleh_boulaares@yahoo.fr, kawlamine@gmal.com,
haiourm@yahoo.fr
Received: 16 May 2016; accepted:
3 January 2017
Abstract. The main purpose of this paper is to analyze the convergence of the proposed algorithm [5] of the finite element methods coupled with a Euler discretization scheme. Also, an optimal error estimate with an asymptotic behavior in uniform norm are given for an evolutionary nonlinear Hamilton Jacobi Bellman (HJB) equation with respect to the Dirichlet boundary conditions.
MSC 2010: 65M80, 35L20
Keywords: QVIs, Finite elements, Theta Scheme Fixed point, HJB equations, Geometric Convergence.
1. Introduction
In this paper, we extend our work [5] and continue to analyze the convergence of the proposed algorithm of the finite element methods coupled with a Euler discretization scheme. In addition, an optimal error estimate with an asymptotic behavior in uniform norm are given, for the following evolutionary nonlinear HJB equation
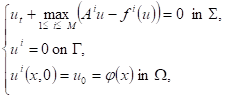 (1)
(1)
where ![]() is a bounded open domain of
is a bounded open domain of ![]() ,
, ![]() with
boundary
with
boundary ![]() sufficiently
smooth and
sufficiently
smooth and ![]() set in
set in ![]() ,
, ![]() with
with ![]() the
the ![]() are given smooth
positive functions, and the
are given smooth
positive functions, and the ![]() are
second-order, uniformly elliptic operators defined over
are
second-order, uniformly elliptic operators defined over ![]()
![]() (2)
(2)
and whose coefficients ![]() are sufficiently
smooth coefficients and satisfy the following conditions
are sufficiently
smooth coefficients and satisfy the following conditions
![]() (3)
(3)
with
![]() (4)
(4)
and the bilinear forms associated with ![]() , for
, for ![]()
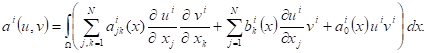 (5)
(5)
![]() is a regular function satisfying
is a regular function satisfying
![]() (6)
(6)
We shall also need the following norm
![]()
Let ![]() be the scalar product in
be the scalar product in ![]()
In (cf. [3]), we applied a new time-space discretization using the semi-implicit time scheme combined with a finite element approximation, we found (1) can be transformed into the following full-discrete HJB equation
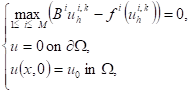 (7)
(7)
where ![]() ,
, ![]() such that
such that ![]() defined on (2),
defined on (2), ![]() , respectively
, respectively ![]()
In [3-5] we proved the theorem of the
geometrical convergence and the existence and uniqueness of the solution of
both the continuous and the discrete HJB equation of the stationary case using
Bensoussan's algorithm. Also, in (cf. [3,4]) the system of parabolic quasi
variational inequalities (PQVIs) can be transformed into a system of the
following full-discrete system of strongly coercive elliptic quasi variational
inequalities (QVIs): find ![]() solution
of
solution
of
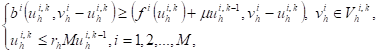 (8)
(8)
with
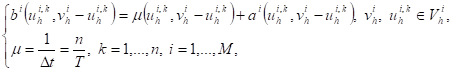 (9)
(9)
where the discrete spaces ![]() of finite element
given by
of finite element
given by
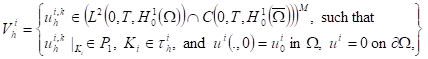 (10)
(10)
where ![]() is the usual interpolation operator defined by
is the usual interpolation operator defined by
![]() (11)
(11)
and ![]() denote the set of all those elements,
denote the set of all those elements, ![]() is the mesh size and
it is regular and quasi-uniform. Moreover, the usual basis of affine functions
is the mesh size and
it is regular and quasi-uniform. Moreover, the usual basis of affine functions
![]()
![]() defined by
defined by ![]() ,
where
,
where ![]() is a sum of
triangulation mesh and
is a sum of
triangulation mesh and ![]() be the M-matrices [8] with generic entries
be the M-matrices [8] with generic entries
![]() (12)
(12)
and ![]() is an operator defined by
is an operator defined by
![]() (13)
(13)
with ![]() and
and ![]() is
a continuous operator from
is
a continuous operator from ![]() into
itself satisfying the following assumptions
into
itself satisfying the following assumptions
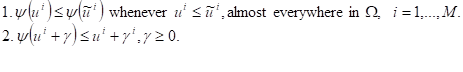
The class of the system of QVIs with
coercive bilinear form includes at least two well-known important problems: the
system of variational inequality of
feedback obstacle (VIs) (when ![]()
![]() and
and ![]() ), and the system of
quasi-variational inequality related to management of energy production (when
), and the system of
quasi-variational inequality related to management of energy production (when ![]() is identically equal
to
is identically equal
to ![]() ,
, ![]() , (cf. [1]).
, (cf. [1]).
The evolutionary HJB equations (1) have many applications in science, engineering and economics; see for example [1] and references therein. They can arise in solving optimal control problems by dynamic programming techniques. Many nonlinear option pricing problems can also be formulated as optimal control problems, leading to HJB equations.
In the last few decades, many numerical
schemes have been proposed for
solving the stationary HJB equations; see for example [7-9] and references
therein. Lions and Mercier [14] presented two iterative algorithms for solving
HJB
equations. At each iteration, a linear complementary subproblem or a linear
equation system subproblem is solved. Boulbrachene and Haiour [6], by means of
a subsolution method, conducted a finite element approximation study for the
first time, for the stationary of the problem (1) and by using
Bensoussan--Lions algorithm [1], a quasi-optimal error estimate in the ![]() - norm has been
derived according the following result
- norm has been
derived according the following result
![]()
In [4], exploiting the above arguments, where we analyzed the theta time scheme combined with a finite element spatial approximation for an evolutionary HJB equation with linear source terms and we derived the following error estimate
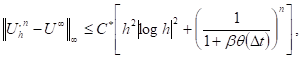
with ![]() a constant independent of both
a constant independent of both ![]() (step of the space discretization) and
(step of the space discretization) and ![]() (step of the time
discretization), where
(step of the time
discretization), where ![]() the
discrete
solution calculated at the moment-end
the
discrete
solution calculated at the moment-end ![]()
![]() and
and ![]() the asymptotic
continuous solution with respect to the right hand side condition. In addition,
we extended the above result [3] to nonlinear case but with the new generalized
space-time discretization stands using the theta scheme and we obtained the
following result
the asymptotic
continuous solution with respect to the right hand side condition. In addition,
we extended the above result [3] to nonlinear case but with the new generalized
space-time discretization stands using the theta scheme and we obtained the
following result
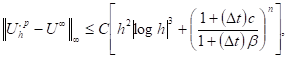
where ![]() is the rate of contraction of the nonlinear source term satisfying
is the rate of contraction of the nonlinear source term satisfying
![]() (14)
(14)
with
![]() (15)
(15)
In this paper, an ![]() -error estimate is
established combining the geometric convergence of discrete iterative schemes
using the known
-error estimate is
established combining the geometric convergence of discrete iterative schemes
using the known ![]() -error
estimates for stationary and evolutionary free boundary problems (cf., e.g.,
[4,6]) which play a major role in the finite element error analysis section.
Finally the asymptotic behavior in uniform norm is deduced which investigated
the evolutionary free boundary problem similar to that in [3].
-error
estimates for stationary and evolutionary free boundary problems (cf., e.g.,
[4,6]) which play a major role in the finite element error analysis section.
Finally the asymptotic behavior in uniform norm is deduced which investigated
the evolutionary free boundary problem similar to that in [3].
The structure of this paper is as
follows. In Section 2 and 3, we consider the discrete system of
quasi-variational inequalities, discretize the iterative scheme by the standard
finite element method combined with a theta scheme and an algorithm iterative
discrete scheme is introduced. Then its geometric convergence is proved with
respect to![]() -stability of
the solution and the right-hand side and its characterization as the least
upper bound of the subsolutions set (see also [5,6]). It is worth mentioning
that this approach is entirely different from the one developed for the
evolutionary problem. Also, it is used for the first time for a system of
stationary QVIs. In Section 4, a fundamental lemma and given optimal error
estimates with an asymptotic behavior in uniform norm are proved for the
presented problem. Finally, we make some comments on the approach and the
results presented in this paper.
-stability of
the solution and the right-hand side and its characterization as the least
upper bound of the subsolutions set (see also [5,6]). It is worth mentioning
that this approach is entirely different from the one developed for the
evolutionary problem. Also, it is used for the first time for a system of
stationary QVIs. In Section 4, a fundamental lemma and given optimal error
estimates with an asymptotic behavior in uniform norm are proved for the
presented problem. Finally, we make some comments on the approach and the
results presented in this paper.
2. The discrete coercive system of QVIs
Definition 1: ![]() is said to
be a subsolution for the system of QVIs (8) if
is said to
be a subsolution for the system of QVIs (8) if
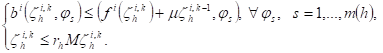 (16)
(16)
Notation 1: Let ![]() be the set of
discrete subsolutions. Then, we have the
following theorem.
be the set of
discrete subsolutions. Then, we have the
following theorem.
Theorem 1: [5] Under the
discrete maximum principle, the solution of the
system of QVI (8) is the maximum element of ![]() .
.
2.1. Existence and uniqueness
2.1.1. A fixed point mapping associated with the system of QVIs
In [3], we have proved the existence and uniqueness of the discrete QVIs (8) using the algorithm based on semi-implicit time scheme combined with a finite element method, which has already been used in our previous research regarding the evolutionary free boundary problems (see [4, 5]).
For that, let us first introduce the
initial vector ![]() where
where
![]() for
for ![]()
![]() is solution of
is solution of
![]() (17)
(17)
where
![]()
Let ![]() , where
, where ![]() denotes
the positive cone of
denotes
the positive cone of ![]() .
.
Now, we consider the mapping
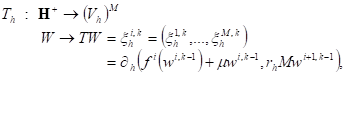 (18)
(18)
where ![]() is solution of the following problem
is solution of the following problem
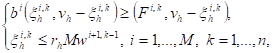 (19)
(19)
where
![]()
2.2. A discrete iterative scheme
Starting from ![]() solution
of (17), we define
solution
of (17), we define
![]() (20)
(20)
and
![]() (21)
(21)
where ![]() is the subsolution of the problem (8).
is the subsolution of the problem (8).
Theorem 2: [5] The
sequences ![]() well
defined in
well
defined in ![]() and
converge to the unique solution of system of inequalities (8).
and
converge to the unique solution of system of inequalities (8).
where
![]() (22)
(22)
2.3. Regularity of sequences of HJB (21)
Theorem 3: (Lewy Stampacchia inequality)[1] Let ![]() be an elliptic
operator defined in (2) and
be an elliptic
operator defined in (2) and ![]() the
solution of an elliptic variational inequalities (VIs) with a simple obstacle
the
solution of an elliptic variational inequalities (VIs) with a simple obstacle ![]() in
in ![]() and the right hand
side
and the right hand
side ![]()
![]() such that
such that ![]() in
the sense of
in
the sense of ![]() , where
, where ![]() Then
Then
![]() (23)
(23)
![]() (24)
(24)
and
![]() (25)
(25)
Lemma 1: For ![]() , we have
, we have
![]() (26)
(26)
where ![]() is a subsolution of the problem (8).
is a subsolution of the problem (8).
Proof: It is clear that
![]()
is the solution of (8) with the obstacle
![]() and the right hand
side
and the right hand
side ![]() and
and ![]()
Since
![]()
then, we have
![]()
where
![]()
Using Lewy Stampacchia inequality, we get
![]()
where ![]() with
with ![]() .
.
Now, we assume that
![]()
then ![]() verify
verify
![]()
and we have ![]() in
in ![]() , then
, then
![]()
3. Geometrical convergence of the discrete algorithm
Lemma 2:[5] For 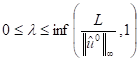 , where
, where ![]() is
a positive constant
defined in (13), then we have
is
a positive constant
defined in (13), then we have
![]() (27)
(27)
Proposition 1: [5] Let
![]() such that
such that
![]() (28)
(28)
then, we have
![]() (29)
(29)
Proposition 2: Under the assumptions and previous notations, we have
![]() (30)
(30)
where ![]() is the subsolution of (8), and
is the subsolution of (8), and ![]() is an asymptotic semi-discrete solution of (1) using the standard
finite element method.
is an asymptotic semi-discrete solution of (1) using the standard
finite element method.
Proof : Using Theorem 2, we have
![]()
then
![]()
Using Proposition 1 with ![]() we get
we get
![]()
or
![]()
Using Proposition 1 again with ![]() , we get
, we get
![]()
i.e.
![]()
and by induction
![]()
Under the third step of the proof of Theorem 3 in [5], we deduce that
![]()
4. Optimal error estimates and asymptotic behavior
Before discussing the results, it is interesting to introduce the result of the following problems
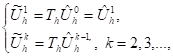 (31)
(31)
where ![]() solution of (17) and
solution of (17) and ![]() is the subsolution of (8).
is the subsolution of (8).
Theorem 4: For all ![]() and
and ![]() is a constant
independent with
is a constant
independent with ![]() ,
we have the following estimate
,
we have the following estimate
![]() (32)
(32)
where ![]() is the subsolution of a semi-discrete problem in time using the
semi-implicit scheme.
is the subsolution of a semi-discrete problem in time using the
semi-implicit scheme.
Proof: The proof is similar to that in [8].
The following lemma will play a crucial role in obtaining the approximation error:
Lemma 3:
For all ![]() and
and ![]() independent by
independent by ![]() we have the following
estimate
we have the following
estimate
![]() (33)
(33)
Proof : By induction, we have
![]()
then
![]()
Since ![]() is Lipschitz, thus
is Lipschitz, thus
![]()
Assume that
![]()
then, we have
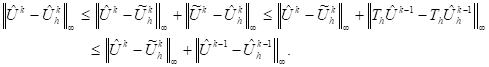
Using the induction assumption, we get
![]()
5. ![]() -optimal error
estimate
-optimal error
estimate
Theorem 5:
For all ![]() and
and ![]() independent by
independent by ![]() , we have the following
estimate
, we have the following
estimate
![]() (34)
(34)
Proof : We have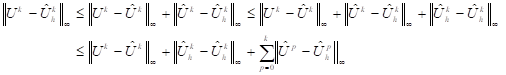
![]()
From the initial data in (1), we have ![]() and
and ![]() then, it can be used
the following standard error estimate [8,9] which investigated the stationary
case
then, it can be used
the following standard error estimate [8,9] which investigated the stationary
case
![]() (35)
(35)
Using the estimates (30), (32) and (35), thus
![]()
Setting
![]()
then
![]()
Therefore, it can be deduced
![]()
Proposition 3: [3] Under the assumption (14), we have for all ![]() the following
estimates
the following
estimates
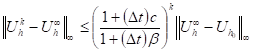 (36)
(36)
Now we evaluate the variation in ![]() - norm between
- norm between ![]() the
discrete solution calculated at the moment
the
discrete solution calculated at the moment ![]() and
and ![]() the
asymptotic continuous solution of (1).
the
asymptotic continuous solution of (1).
Theorem 6: Under the results of Proposition 3 and Theorem 5, we have for
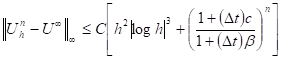 (37)
(37)
Proof: Using Theorem 5 and Proposition 3, it can be easily obtained
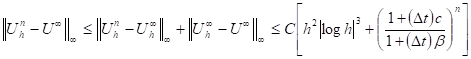
which completes the proof.
6. Conclusions
In this paper, the regularity and convergence of the presented algorithm sequences of the finite element methods coupled with the Euler time discretization scheme are analyzed. Also, an optimal error estimate with asymptotic behavior in a uniform norm are given for an evolutionary HJB equation with respect to the same proposed boundary conditions in [4]. A next paper will propose a decomposition methods for solving these problems. The convergence of the new scheme will be established and the numerical example will be shown to prove that the new presented scheme is efficient.
Acknowledgement
The first author gratefully acknowledge Qassim University in Kingdom of Saudi Arabia and this presented work in memory of his father (1910-1999) Mr. Mahmoud ben Mouha Boulaaras. All authors of this paper would like to thank the anonymous referees and the handling editor for their careful reading and for relevant remarks/suggestions which helped him to improve the paper.
References
[1] Bensoussan. A, Lions. J.L., Applications des inequations variationnelles en controle stochastique, Dunod Paris 1978.
[2]
Boulaaras.S, Haiour. M., ![]() asymptotic behavior for a finite element
approximation in parabolic quasi-variational inequalities related to impulse
control problem, Appl. Math. Comput. 2011, 217, 6443-6450.
asymptotic behavior for a finite element
approximation in parabolic quasi-variational inequalities related to impulse
control problem, Appl. Math. Comput. 2011, 217, 6443-6450.
[3] Boulaaras.S, Haiour. M., The finite element approximation of evolutionary Hamilton--Jacobi--Bellman equations with nonlinear source terms, Indagationes Mathematicae. 2013, 24, 161-173.
[4] Boulaaras.S, Haiour. M., The theta time scheme combined with a finite element spatial approximation of Hamilton-Jacobi-Bellman equation, , Comput. Math. Model. 2014, 25, 423-438.
[5] Boulaaras.S, Haiour. M., The finite element approximation of evolutionary Hamilton–Jacobi–Bellman equations with nonlinear source terms, Ind. Math. 24 (2013) 161–173
[6] Boulbrachene. M, Haiour. M., The finite element approximation of Hamilton Jacobi Bellman equations, Comput. Math. Appl. 2001, 41, 993-1007.
[7] Cortey-Dumont. P., Sur I' analyse numerique des equations de Hamilton-Jacobi-Bellman, Math. Meth. in Appl. Sci, (1987).
[8]
Cortey-Dumont. P., On the finite element
approximation in the ![]() -norm of variational
inequalities with nonlinear operators, Numer. Math., 1985, 47 , 45-57.
-norm of variational
inequalities with nonlinear operators, Numer. Math., 1985, 47 , 45-57.
[9]
Nitsche. J., ![]() -convergence
of finite element approximations, Mathematical aspects of finite element
methods, Lect. Notes. Math. 1977, 606, 261-274.
-convergence
of finite element approximations, Mathematical aspects of finite element
methods, Lect. Notes. Math. 1977, 606, 261-274.
[10] Ciarlet. P., Raviart. P., Maximum principle and uniform convergence for the finite element method. Com. Math. Appl. Mech. Eng. 1973, 2, 1-20.
[11] Evans. L. C., Classical solutions of the Hamilton-Jacobi-Bellman equation for uniformly elliptic operators, Trans. Amer. Math. Soc. 1983, 275, 245-255.
[12] Evans. L. C, Friedman. A., Optimal stochastic switching and the Dirichlet problem for the Bellman equations, Trans. Amer. Math. Soc. 1979, 253, 365-389.
[13] Lions. P. L, Menaldi. J. L., Optimal control of stochastic integrals and Hamilton Jacobi Bellman equations, (Part I), SIAM. J. Control. Optim. 1979, 20.
[14] Lions. P. L, Mercier . B., Approximation numérique des equations de Hamilton Jacobi Bellman, RAIRO, Anal. Num. 1980, 14, 369-393.

