Relationships between the permanents of a certain type of k-tridiagonal symmetric Toeplitz matrix and the Chebyshev polynomials
Ahmet Zahid Küçük
,Murat Düz
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
RELATIONSHIPS BETWEEN THE PERMANENTS OF A CERTAIN TYPE OF k-TRIDIAGONAL SYMMETRIC TOEPLITZ MATRIX AND THE CHEBYSHEV POLYNOMIALS
Ahmet Zahid Küçük 1, Murat Düz 2
1 Eskipazar
Vocational School
Turkey
2 Department of Mathematics Faculty of Science, Karabuk University
Turkey
azahidkucuk@karabuk.edu.tr, mduz@karabuk.edu.tr
Received: 16 December 2016; accepted:
13 March 2017
Abstract. In this study, the recursive relations between the permanents of a certain type of the k-tridiagonal symmetric Toeplitz matrix with complex entries and the Chebyshev polynomials of the second kind are presented.
MSC 2010: 33C45
Keywords: permanent, Toeplitz matrix, k-tridiagonal matrix, Chebyshev polynomials, recurrence relation
1. Introduction
A k-tridiagonal symmetric Toeplitz matrix can be written in the form
where
 . . | (1) |
The Toeplitz structured tridiagonal matrix family can be seen with many studies in different areas. Some of them include the solution of ordinary and partial differential equations [1] in the applied mathematics, including the equilibrium problem [2] in the statistical physic, wireless and sensor network applications [3, 4] about control theory in computer sciences and the sensitivity of MRNA [5] in molecular biology.
The aim of this study is to point out some relationships between the permanents of the certain type of k-tridiagonal symmetric Toeplitz matrix and the Chebyshev polynomials of the second kind. The definition of the k-tridiagonal symmetric Toeplitz matrix that is used in this study is given below.
Definition: Let the k-tridiagonal
symmetric Toeplitz matrix ![]() of order
of order ![]() with
first row be
with
first row be ![]()
 | (2) |
![]() ,
, ![]() and
and ![]() are positive integers such
that
are positive integers such
that ![]()
The matrix ![]() was
pronounced as the tridiagonal instead of the k-tridiagonal throughout in
this study. Also, it is worth noting that if
was
pronounced as the tridiagonal instead of the k-tridiagonal throughout in
this study. Also, it is worth noting that if ![]() and
and ![]() then the
then the ![]() and
and ![]() matrices convert a pentadiagonal and
heptadiagonal matrix respectively. But, this nomenclature for
matrices convert a pentadiagonal and
heptadiagonal matrix respectively. But, this nomenclature for ![]() was not used in this study.
was not used in this study.
In the literature, much research has been gathered on the relationships between the permanent or determinant of some tridiagonal or Toeplitz matrices and the famous number sequences or the linear recurrences. For example, Minc [6] gave a recursive formula for the permanent of a general tridiagonal Toeplitz matrix. Lehmer [7] demonstrated some generalizations for the permanent of a tridiagonal matrix by using expansion by minors. Kılıc and Tascı [8] presented some relationships between the permanents of some tridiagonal matrices and some famous number sequences. Jina and Trojovsky [9] presented new results about the relationships between the permanents of some tridiagonal matrices and the Fibonacci numbers. Matousova and Trojovsky [10] showed a generalization for sequences of tridiagonal matrices which is related to the sequence of Fibonacci numbers. Kaygısız and Sahin [11] obtained the permanents of some tridiagonal matrices with complex elements in terms of k sequences of generalized order-k Fibonacci numbers. Kırklar and Yılmaz [12] gave an important representation for the permanent of a k-tridiagonal k-Toeplitz matrix by using the direct sum of the matrices. Yılmaz and Bozkurt [13] gave one type of tridiagonal matrix whose permanents are Jacobsthal numbers. Of course, the studies on the determinants of special matrices take more space than on the permanents of these matrices. We focused on the few that are closest to our study. Elouafi [14] gave the formulas which involve determinants whose entries are the Chebyshev polynomials for a banded symmetric Toeplitz matrix. Cahill et al. [15] showed some special tridiagonal matrices whose determinant gives the Chebyshev polynomials. Kılıç [16] presented the two different representations depending on the parity of n for the permanent of general 2-tridiagonal Toeplitz matrix that emblematized this matrix with H(a,b,-c). Asci, Tasci and Al-Mikkawy [17] gave algorithms for permanents of k-tridiagonal matrices using LU factorization. In Trench [18] gave a recursive relation for the eigenvalues of a 2-tridiagonal Toeplitz matrix. Bergun and Hoggatt [19] gave the recursive relations among the determinants of a general tridiagonal, 2-tridiagonal and 3-tridiagonal Toeplitz matrix and also gave a representation for the determinant of the general k-tridiagonal Toeplitz matrix with respect to the determinant of the tridiagonal Toeplitz matrix. Our study focuses on the relationships between the permanents of a certain type of k-tridiagonal symmetric Toeplitz matrix with complex entries and the Chebyshev polynomials of the second kind.
Chebyshev polynomials being a useful mathematical tool, are often utilized in the mathematics as well as other fundamental science and the engineering. Chebyshev polynomials of the second kind is a polynomial of degree n in x defined in [20] by
where ![]() . The family of the Chebyshev polynomial
of the second kind
. The family of the Chebyshev polynomial
of the second kind ![]() satisfies the recurrence
relation
satisfies the recurrence
relation
| (3) |
where ![]() ,
, ![]() ,
, ![]() . We have referred to Chebyshev
polynomials of the second kind as Chebyshev U polynomials throughout in
this study. The first few Chebyshev U polynomials are
. We have referred to Chebyshev
polynomials of the second kind as Chebyshev U polynomials throughout in
this study. The first few Chebyshev U polynomials are
 | (4) |
Let ![]() be the symmetric group which
consist of all permutations of
be the symmetric group which
consist of all permutations of ![]() and
and ![]() be the element of this group where
be the element of this group where ![]() . Then, the permanent of an
. Then, the permanent of an ![]() square
matrix
square
matrix ![]() is defined by
is defined by
| (5) |
The permanent is a function of the matrix elements such as the determinant without using signs for the permutations. For this reason, some operations that are applied on the determinant can also be used on the permanent. The Laplace expansion is one of these operations. We note that all of the signs used in the Laplace expansion of minors are positive. It should be noted that we used the Laplace expansion for the permanent throughout in this study. Despite gaining more prominence in the recent studies on the permanent such as in [12], the contraction method, which is given by Brualdi and Gibson [5], doesn’t work for the permanent of a complex matrix.
2. Main results
2.1. Relationships between
![]() and the Chebyshev U
polynomial
and the Chebyshev U
polynomial
Theorem 1: The
permanent of the matrix ![]() is
is
| (6) |
where ![]() is the nth Chebyshev U
polynomials and
is the nth Chebyshev U
polynomials and ![]() .
.
Proof: We will use mathematical induction method in this proof.
For ![]()
 |
Thus (6) is provided. Assume that the equality (6) holds for n. So, we have
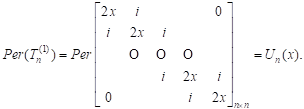 | (7) |
We will now show that
equality (6) holds for ![]() , namely
, namely
| (8) |
Firstly,
we expand the ![]() by
using the Laplace expansion according to the first row
of
by
using the Laplace expansion according to the first row
of ![]() . Then, we obtain
. Then, we obtain
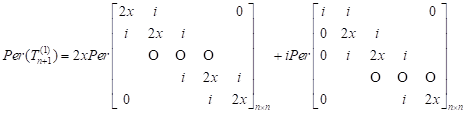 . . |
Secondly, we expand the permanent which appears in the second term of the right hand side of the above equation with respect to its first column. So, we obtain
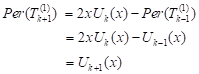 | (9) |
which is desired.
Theorem 2: The
permanent of the matrix ![]() is
is
 | (10) |
where ![]() is the nth Chebyshev U polynomials and
is the nth Chebyshev U polynomials and ![]() .
.
Proof: We will use the mathematical induction method for the proof.
Suppose that ![]() . Then
. Then
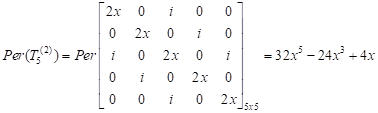 |
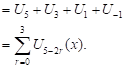
Thus, the equality (10) is true for ![]() . Assume that
the equality (10) holds for n, i.e.
. Assume that
the equality (10) holds for n, i.e.
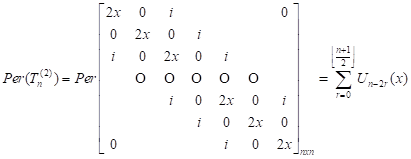 . . | (11) |
We will now show that the equality (10) is also
true for ![]() , namely
, namely
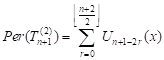 . . | (12) |
Let us write
![]() by using the Laplace expansion with
respect to its first
column. Then
by using the Laplace expansion with
respect to its first
column. Then
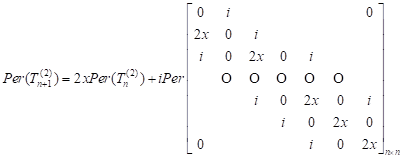 | (13) |
Let’s expand the permanent that appears in the second term of right hand side of the equality (13) with respect to its first row. So, we have:
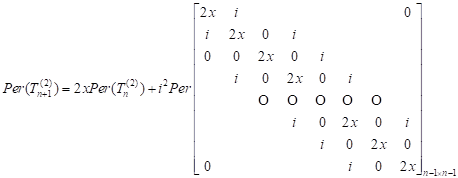 | (14) |
If the permanent appears in the second term of
right hand side of the (14) is
expanded with respect to the its first row, then ![]() will
be equal to
will
be equal to
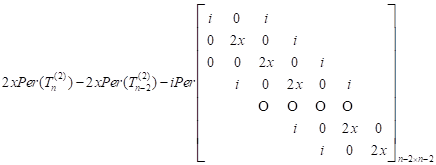 | (15) |
Lastly, we expand the permanent that appears in the third term of right hand side of the (15) with respect to its first column. So, we obtain
| (16) |
We rewrite the equality (16) by using (11),
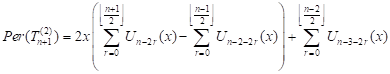 | (17) |
We have two cases depending on the parity of n. Let n be odd. If we arrange the equality (17), then we get the following result (18).
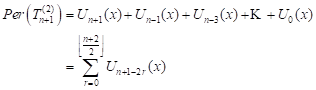 | (18) |
It is easy to see that the result (18) is obtained also if n is even. Thus, the proof is completed.
Theorem 3: There is a representation for the
Chebyshev U polynomials in terms of the permanent of ![]() as following:
as following:
| (19) |
| where |
Proof: Using Theorem 2, we write that
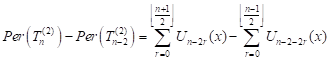 . . | (20) |
If we replace the upper limit of the first
summation in the equality (20) with ![]() So, the equality
(20) will take the form of
So, the equality
(20) will take the form of
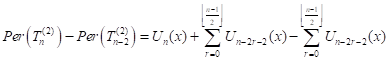 | (21) |
such that the right side of (21) is equal to ![]() .
.
Conjecture 4:
For ![]()
| (22) |
and for ![]()
| (23) |
where ![]() is the nth
Chebyshev U polynomial.
is the nth
Chebyshev U polynomial.
Because of that becomes difficult obtaining of
the representations with respect
to the Chebyshev U polynomials
for each ![]() values of
values of ![]() , the study will continue
the following section.
, the study will continue
the following section.
2.2. The Recursive
Formulas for ![]()
In accordance with the Theorem 1, it can be
seen that the defining recurrence of the Chebyshev U polynomials, given
by (3), is true for ![]() .
.
Result 5: For ![]()
![]() (24)
(24)
where ![]() ,
, ![]() .
.
Hereby, we should emphasize that also the equality (16), which is a natural result of the Theorem 2, is actually a recursive formula as like (24). This is stated below.
Result 6: For ![]()
with initial conditions ![]() ,
, ![]() ,
, ![]() and
and ![]() .
.
Proof: If the equalities (6) and (19) uses together in the equality (24) then the expression which is numbered in the first section with (16) can be obtained.
Theorem 7: If ![]() is
is ![]() integer then
integer then
| (25) |
is true such that ![]() ,
, ![]() .
.
Proof: It is easily proven using the induction
method by ![]() .
.
Firstly, we must
demonstrate the equality (25) is true for ![]() , i.e.
, i.e.
| (26) |
By using the Theorem 2, the left side of the equality (26) is ![]() which yields to
which yields to ![]() . Likewise, the right side of the
equality (26) is
. Likewise, the right side of the
equality (26) is ![]() which also yields to
which also yields to ![]() . Thus, it is easy to see that the both
sides of (26) are equal to each other.
. Thus, it is easy to see that the both
sides of (26) are equal to each other.
Now, assume that
the equality (26) holds for ![]() , i.e.
, i.e.
| (27) |
where ![]() . We will show that the equality (26)
also holds for
. We will show that the equality (26)
also holds for ![]() .
If equality (16) is rewritten by putting
.
If equality (16) is rewritten by putting ![]() instead of
instead of ![]() , then
, then
| (28) |
is obtained. If the equality (27) into consideration in the equality (28), then
is obtained which is desired.
Now let
us demonstrate the generalization we obtained for ![]() .
.
Conjecture 8:
If ![]() then
then
| (29) |
where ![]() and
and ![]() .
.
In examinating the Conjecture 8, firstly the
value of ![]() is assignment, then the values of
is assignment, then the values of ![]() are assingment.
are assingment.
Remark 9: According to the Conjecture 8, it can be
clearly stated that ![]() ,… cannot be written in terms
of themselves like the recurrence (16) which is emphasized as the Result 6.
,… cannot be written in terms
of themselves like the recurrence (16) which is emphasized as the Result 6.
Let’s explain this
remark by giving an example. In the case of ![]() ,
, ![]() becomes equal to
becomes equal to![]() . So, it can be obtained following equalities for the first
few values of
. So, it can be obtained following equalities for the first
few values of ![]() :
:
| (30) |
| (31) |
| (32) |
| (33) |
None of the terms of these equations (30),
(31), (32), (33) is repeated in another equation. So, it's the evidence that
the recursive formula which is written for ![]() in
terms of itself and is provided for all consecutive
in
terms of itself and is provided for all consecutive ![]() values cannot be obtained.
values cannot be obtained.
However, a recursive representation for ![]() given below was obtained.
given below was obtained.
Conjecture 10: Let ![]() and
and ![]() be the positive integers and
be the positive integers and ![]() . Then
. Then
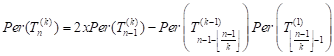 | (34) |
where ![]() .
.
Result 11: Taking into account the Conjecture 8 and the Conjecture 10 we get
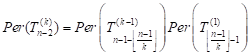 | (35) |
where ![]() and
and ![]() is a positive integer. If the equality (35) is rearranged by taking
into the Theorem 1 consideration, we obtain the representation of Chebyshev U
polynomials in terms of the permanent of
is a positive integer. If the equality (35) is rearranged by taking
into the Theorem 1 consideration, we obtain the representation of Chebyshev U
polynomials in terms of the permanent of ![]() as
follows:
as
follows:
| (36) |
where ![]() and
and ![]() is the positive integer and
is the positive integer and ![]() is the rth Chebyshev U polynomials.
is the rth Chebyshev U polynomials.
As an example of
using the equality (35), let’s take the ![]() :
:
| (37) |
So, we get
respectively for ![]() .
.
3. Conclusions
In this study, it can be seen that the Chebyshev polynomials can be expressed in terms of the permanents of tridiagonal k-Toeplitz matrices which are both band and circulant matrices.
Additionally, some recursive relations for the permanent of the certain type of k-tridiagonal symmetric Toeplitz matrix as conjectures are given.
It can be seen that the recursive representations obtained in this study are similar to the results in the [19].
As a
further study, the representation of ![]() with respect to the Cheby-
shev polynomials can be generalized for
with respect to the Cheby-
shev polynomials can be generalized for ![]() in the Section
2.1.
in the Section
2.1.
References
[1] Mazilu I., Mazilu D.A., Williams H.T., Applications of tridiagonal matrices in non-equilibrium statistical physics, Electronic Journal of Linear Algebra 2012, 24, 7-17.
[2] Fontanelli D., Palopoli L., Passerone R., On the Global Convergence of a Class of Distributed Algorithms for Maximizing the Coverage of a WSN, 28th Chinese Control Conference, Shanghai 2009 (IEEE, 2009), 7885-7890.
[3] Martínez S., Bullo F., Cortés J., Frazzoli E., On synchronous robotic networks - Part I: Models, tasks, and complexity, IEEE Transactions On Automatic Control 2007, 52(12).
[4] Poker G., Margaliot M., Tuller T., Sensitivity of mRNA translation, Scientific Reports 5, Article number: 12795, (2015).
[5] Brualdi R.A., Gibson P.M., Convex polyhedra of doubly stochastic matrices. I: Applications of the permanent function, The Journal of Combinatorial Theory A 1977, 22, 194-230.
[6] Minc H., On permanents of circulants, Pacific Journal of Mathematics 1972, 42(2).
[7] Lehmer D., Fibonacci and related sequences in periodic tridiagonal matrices, Fib. Quart. 1975, 13, 150-158.
[8] Kilic E., Tasci D., On the permanents of some tridiagonal matrices with applications to the Fibonacci and Lucas numbers, Rocky Mountain J. Math. 2007, 37(6), 1953-1969.
[9] Jina J., Trojovsky P., On permanents of some tridiagonal matrices connected with Fibonacci numbers, International Journal of Pure and Applied Mathematics 2014, 97(1), 79-87.
[10] Matousova I., Trojovsky P., On a sequence of tridiagonal matrices, whose permanents are related to Fibonacci and Lucas numbers, International Journal of Pure and Applied Mathematics 2015, 105(4), 715-723.
[11] Kaygısız K., Sahin A., Determinant and permanent of Hessenberg matrix and Fibonacci type Numbers, Gen. Math. Notes 2012, 9(2), 32-41.
[12] Kırklar E., Yılmaz F., A note on k-tridiagonal k-Toeplitz matrices, Alabama Journal of Mathematics 2015, 39.
[13] Yılmaz F., Bozkurt D., The adjacency matrix of one type of directed graph and the Jacobsthal numbers and their determinantal representation, Journal of Applied Mathematics 2012.
[14] Elouafi M., On a relationship between Chebyshev polynomials and Toeplitz determinants, Applied Mathematics and Computation 2014, 229, 27-33.
[15] Cahill N.D., Derrico J.R., Spence J.P., Complex factorizations of the Fibonacci and Lucas numbers, Fibonacci Quarterly 2003, 41(1), 13-19.
[16] Kılıç E., On a constant-diagonals matrix, Applied Mathematics and Computation 2008, 204(1), 184-190.
[17] Asci M., Tasci D., El-Mikkawy M., On determinants and permanents of k-tridiagonal Toeplitz matrices, Util. Math. 2012, 89, 97-106.
[18] Trench W.F., Banded Symmetric Toeplitz Matrices (Lecture of Mathematic Seminar, Trinity University, 2009).
[19] Bergun G.E., Hoggatt V.E., A family of tridiagonal matrices, Fibonacci Quart. 1978, 16, 285-288.
[20] Mason J.C., Handscomb D.C., Chebyshev Polynomials, Chapman Hall/CRC, Boca Raton 2003.

