Variations on the arbelos

VARIATIONS ON THE ARBELOS

Michał Różański, Alicja Samulewicz, Marcin Szweda, Roman Wituła

Institute of Mathematics, Silesian University of Technology Gliwice, Poland Michal.Rozanski@polsl.pl, Alicja.Samulewicz@polsl.pl Marcin.Szweda@polsl.pl, Roman.Witula@polsl.pl

Received: 12 April 2017; accepted: 18 May 2017

Abstract. We recall the ancient notion of arbelos and introduce a number of concepts gene-ralizing it. We follow the ideas presented by J. Sondow in his article on parbelos, the parabolic analogue of the classic arbelos. Our concepts concern the curves constructed of arcs which resemble each other and surfaces obtained in a similar way. We pay special attention to ellarbelos, the curves built of semi-ellipses, because of their possible application in engineering, e.g. in determining the static moments of arc rod constructions or in problems of structural stability and durability of constructions.

MSC 2010: 51N20, 51M25

Keywords: arbelos, parbelos, similarity, ellarbelos, F-arbelos

1. Introduction

The starting point of this article was a discussion on the parabolic analogue of arbelos described in [1]. We tried to find other ways of generalizing this notion and we investigated the relationships between them. Since the issue was rather elementary, the students had the opportunity to work on a par with more experienced mathematicians and all involved enjoyed this cooperation. Some of our interpretations of the ancient subject are described in the following.

The first two sections contain a short summary of the properties of arbelos and parbelos, followed by a presentation of the results of our efforts and the questions that arose during the discussion. We consider elliptic analogues of the classic arbelos, namely the figures bounded by three semi ellipses which are pairwise tangent, but not necessarily similar. We give a necessary and sufficient condition for the semi ellipses for being tangent. Then we show a relationship between the area of the ellarbelos and the areas of certain ellipses associated to the ellarbelos. Finally, we present our attempts at defining three-dimensional analogues of arbelos.

2. Antique origin

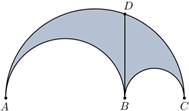
An arbelos is a plane figure bounded by three semicircles that are pairwise tangent and have diameters lying on the same line (see Figure 1). Its name comes from Greek and means shoemaker's knife. The first known mention of the figure can be found in the ancient Book of Lemmas [2] which includes a number of propositions, attributed to Archimedes of Syracuse and concerning the properties of circles.

The common points of two semicircles of the arbelos are called the cusps and labeled A, B, C, where AC is the diameter of the largest semicircle.

Fig. 1. Arbelos

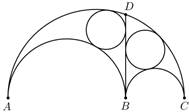
Fig. 2. Twin Circles of Archimedes

Property 2.1. The length of the upper boundary of an arbelos is equal to the length of its lower boundary.

Property 2.2. Under each lower arc of an arbelos construct a new arbelos similar to the original one. Of the four new lower arcs, the middle two are congruent and their common length equals one half the harmonic mean of the lengths of the original lower arcs.

Property 2.3. Let D be the common point of the outer semicircle and the line perpendicular to AB through B. Then the area of the arbelos is equal to the area of the circle whose diameter is BD.

Property 2.4. The middle cusp and the midpoints of the semicircular arcs of an arbelos determine a rectangle whose area equals times the area of the arbelos.

Property 2.5. Let the segment BD be perpendicular to AB and divide the arbelos into two regions, each of them bounded by this segment, a semicircle and an arc of the largest semicircle. Then the circles inscribed in these regions, known as the Twin Circles of Archimedes, are congruent.

More facts concerning the arbelos can be found in [3-6]; furthermore [4] provides an interesting historical overview of the subject.

3. Inspired by the classic: parbelos

The notion of arbelos can be generalized by taking three arcs that are all similar to each other instead of semicircles. In [1], semicircles are replaced by the latus rectum arcs of parabolas to obtain a parabolic analog of the arbelos, referred to as parbelos by the author. Recall that the latus rectum of a parabola is the chord passing through the focus and parallel to the directrix. The latus rectum arcs of all parabolas are similar, as with all semicircles. The smaller arcs of the parbelos are tangent to the largest one, but they are not tangent to each other.

It turns out that the parbelos have several properties related to those of the arbelos.

Property 3.1. The upper and the lower boundaries of a parbelos have the same length.

Property 3.2. Under each lower arc of a parbelos construct a new parbelos similar to the original. Of the four new lower arcs, the middle two are congruent and their common length equals one half the harmonic mean of the lengths of the original lower arcs.

Property 3.3. The middle cusp of a parbelos and the vertices of its three parabolas determine a parallelogram whose area equals times the area of the parbelos.

4. A step further

In order to obtain a further class of figures resembling arbelos one can consider arcs of other shapes instead of semicircles.

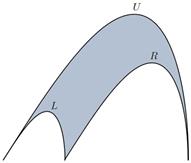
Fix the points A(0,0), B(b,0), C(a,0) with 0<b<a and consider three arcs U, R, L contained in the upper half-plane ℝ and such that A, C are the ends of U, the points A, B are the ends of L and B, C are the ends of R. Assume that U, R, L are pairwise disjoint apart from their common ends. Then the curve is the boundary of a plane region and can be called the generalized (U,R,L)-arbelos.

One can consider (U,R,L)-arbelos where the upper arc U is the graph of a continuous function with , 0 < b < a, and the lower boundary of the figure consists of the graphs L and R of functions and , respectively (see Figure 3).

To avoid intersecting U by the arcs L and R (except the points (0,0) and (a,0)) it is necessary to assume that

(1)

If U is the graph of a continuous function with then the U-arbelos is also called the F-arbelos or the F-belos ([7], [8]). Note that the classic arbelos and parbelos belong to this class.

The case of U being the graph of a continuous function has been deeply investigated in [7] and [8], where one can find more properties of F-arbelos and examples, including hyperbolic analogues of arbelos.

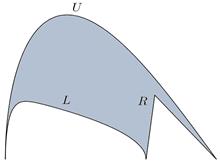
Fig. 3.

Fig. 4. F-arbelos built of the lemniscate of Gerono (on the left) and F-arbelos built of non-convex function (on the right)

It turns out that the class of (U,R,L)-arbelos bounded by three similar arcs U, L and R (which are not necessarily the graphs of real-valued functions) also satisfies Properties 2.1, 3.1, 2.2, 3.2 and the conditions corresponding to Properties 2.4 and 3.3.

5. Ab ovo et ad ovum: elliptic arbelos

Now consider elliptic arbelos or ellarbelos, the class of figures whose boundaries consist of three semi ellipses instead of three semicircles.

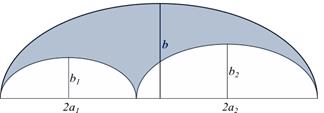
Fig. 5. Elliptic arbelos

We can assume that all considered ellipses are symmetric about the x-axis, however their major axes are not necessarily parallel. Then the arcs U, L, R forming the boundary of the ellarbelos are the graphs of the appropriate functions F, and (see Section 4). In particular, if all semi ellipses are pairwise similar then the ellarbelos is an F-arbelos and possesses all the properties mentioned in Section 4.

In the definition of the ellarbelos, we do not assume that the semi ellipses are similar, but we require that both the L and R arcs meet the arc U in exactly one point.

Consider ellipses

(2)

where are positive numbers, and

Assume that and are pairwise tangent and the curves are contained in the closed region bounded by E. Then

(3)

Let and be the parametrizations of the semi ellipses and respectively. We intend to find conditions assuring that has only one common point with E. Since the largest ellipse E is symmetric about the y-axis, we can restrict our consideration to and

Define an auxiliary function putting

Clearly is contained in the closed region bounded by E if and only if for all Notice that

(4)

is a quadratic polynomial and

(5)

Note that . Therefore, if on then must be decreasing on an interval for some . Hence The latter is equivalent to

(6)

Now assume that (6) holds. If the coefficient of t in the equality (5) is non-positive, i.e. if

(7)

then on and is a strictly decreasing function with Thus for all

On the other hand, if

(8)

then (5), (6) and (8) imply that is an increasing linear function with so for all This means that is decreasing and, since all its values are non-negative.

Recapitulating, on if and only if (6) holds.

Lemma 5.1. Three ellipses

are pairwise tangent if and only if

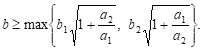(9)

Henceforth we assume that the semi ellipses forming the ellarbelos satisfy the condition (9).

Example 5.2. The borderline case of (9) is The ellarbelos satisfying this condition, namely with is depicted in Figure 6. Enlarging the value of or would result in an output of or beyond the region bounded by E.

Fig. 6. Ellarbelos with optimally selected parameters

Property 5.3. The area of ellarbelos equals

The above equality is shown in Figure 7.

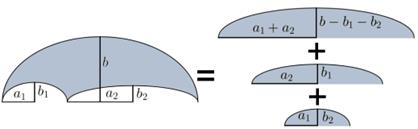
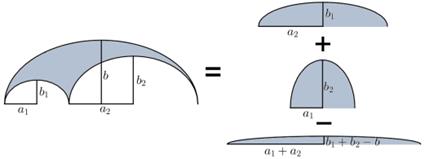
Fig. 7. Illustrations for the above properties for ellarbelos, on the left side, when b > b₁+b₂, on the right side, when b < b₁+b₂

In particular, the area of the classic arbelos is equal to the area of the ellipse whose semiaxes correspond to the radii of the smaller semicircles (see Fig. 8).

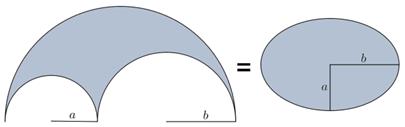
Fig. 8. Illustration for the above properties for arbelos

Remark 5.4. If all semi ellipses bounding an ellarbelos are similar, then there is a shear mapping that transforms it into an arbelos. Thus for every ellarbelos of this kind, there exist two congruent ellipses that are pre-images of the twin circles of Archimedes associated with the arbelos.

Question 5.5. Assume that all semi ellipses enclosing an ellarbelos are similar. For which eccentricities do all ellarbelos have twin circles corresponding to the twin circles of Archimedes? Does the answer depend on whether the foci of all ellipses are colinear () or not ()?

6. Space: above and beyond

By a simple 3D-elliptic arbelos, or briefly 3D-ellarbelos, we mean the upper half of the solid obtained by rotating an ellarbelos around the x-axis (see Fig. 9). In other words, 3D-ellarbelos is enclosed by the plane and three pairwise tangent ellipsoids of revolution. We assume additionally that and i.e. all ellipsoids are prolate spheroids or spheres. The 3D-ellarbelos is regular provided that the semiellipsoids enclosing it are similar.

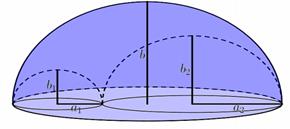
Fig. 9. 3D-elliptic arbelos

The area of the prolate ellipsoid with the semi-principal axes a, b, b equals

(10)

where is the eccentricity of the ellipse.

The difference between the upper surface and the lower one equals

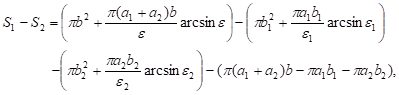where are the eccentricities of the ellipses respectively.

In particular, if all the eccentrities are equal then

(11)

and

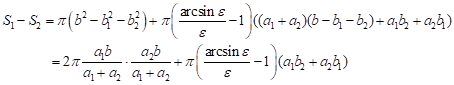where Note that as

If all the ellipses are circles then

According to Property 5.3, is the area of the arbelos bounded by semicircles of radii

Property 6.1. If all semi ellipsoids enclosing 3D-ellarbelos are hemispheres, then the difference between the areas of the upper surface and the lower one equals double the area of the arbelos bounded by semicircles of the same radii as the hemispheres.

Property 6.2. The regular 3D-ellarbelos has the same volume as the cylinder whose base is the revolved ellarbelos and the height equals the diameter of the ellarbelos (see Fig. 10).

Proof: Denote by V and , respectively, the volumes of the regular 3D-ellarbelos and the largest semiellipsoid. Then

where By (4) the area of the ellarbelos equals so indeed

ÿ

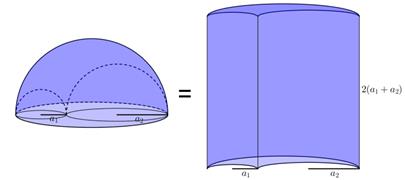
Fig. 10. Equal volumes for a 3D-arbelos composed of spheres and an arbelosoidal cylinder

One can claim that increasing the dimension should result in increasing the number of spheres. However, the case with four pairwise tangent hemispheres seems much more complicated than the ones considered previously. Even determining the relationships between their radii is more complex.

Denote by R the radius of the outer sphere and by the radii of the inner spheres. Using Heron's formula to calculate the areas of the appropriate triangles, we obtain

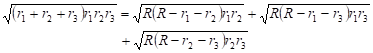(12)

and, consequently,

(13)

The formula (13) can be derived from Descartes' theorem as well ([9, chapter 4.1]):

where and

Question 6.3. Which properties of abelos (parbelos, F-arbelos, ellarbelos, 3D-ellarbelos) have 3D-arbelos with four spheres?

7. Conclusions

The present paper concerns the generalizations of the ancient notion of arbelos. The analogues known from other articles (parbelos, F-arbelos) have been briefly described. We discuss in detail elliptic arbelos (ellarbelos). As far as we know, they can be useful in determining the static moments of arc rod constructions or in problems of structural stability and durability of constructions. We also undertook an attempt of generalizing the notion of arbelos to the three-dimensional case, nevertheless there is still a number of problems we are going to proceed to study. We hope that our results may be helpful to engineers, especially mechanical ones, and we look forward to being inspired by their work.

References

[1] Sondow J., The parbelos, a parabolic analog of the arbelos, Amer. Math. Monthly 2013, 120, 10, 929-935.

[2] Archimedes, Book of Lemmas, The Works of Archimedes, Cambridge University Press, 2009.

[3] Bankoff L., Are the twin circles of Archimedes really twins? Math. Magazine 1974, 47, 4, 214- -218.

[4] Boas H.P., Reflections on the arbelos, Amer. Math. Monthly 2006, 113, 3, 236-249.

[5] Dodge C.W., Schoch T., Woo P.Y., Yiu P., Those ubiquitous Archimedean circles, Math. Magazine 1999, 72, 3, 202-213.

[6] Weisstein E.W., Arbelos [online], MathWorld - A Wolfram Web Resource, http://mathworld. wolfram.com/Arbelos.html.

[7] Oller-Marcén A.M., The f-belos, Forum Geometricorum 2013, 13, 103-111, http://forumgeom.fau.edu/FG2013volume13/FG201310.pdf

[8] Khelif H., L'ARBELOS. PARTIE II, Généralisations de l'arbelos. Présentation et généralisations du salinon, 12.02.2014, http://images.math.cnrs.fr/L-arbelos-Partie-II.html?lang=fr

[9] Kirillov A.A., A Tale of Two Fractals, Birkhäuser, New York 2013.