Cauchy-Binet type formulas for Fredholm operators
Grażyna Ciecierska
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
CAUCHY-BINET TYPE FORMULAS FOR FREDHOLM OPERATORS
Grażyna Ciecierska
Faculty of Mathematics and Computer
Science, University of Warmia and Mazury in Olsztyn
Olsztyn, Poland
grac@matman.uwm.edu.pl
Received: 19 September 2016; accepted: 4 June 2017
Abstract.
Suppose ![]() ,
, ![]() are Fredholm
operators acting in linear
spaces. By referring to the correspondence between
Fredholm operators and their determinant systems, we derive the formulas for a
determinant system for AB which are expressed via determinant systems
for A and B. In our approach, applying results of the theory of
determinant systems plays the crucial role and yields Cauchy-Binet type
formulas. The formulas are utilized in many branches of applied science and
engineering.
are Fredholm
operators acting in linear
spaces. By referring to the correspondence between
Fredholm operators and their determinant systems, we derive the formulas for a
determinant system for AB which are expressed via determinant systems
for A and B. In our approach, applying results of the theory of
determinant systems plays the crucial role and yields Cauchy-Binet type
formulas. The formulas are utilized in many branches of applied science and
engineering.
MSC 2010: 47A53, 15A15
Keywords: Fredholm operator, determinant system, reflexive generalized inverse, Cauchy- -Binet theorem
1. Introduction
The purpose of this paper is to exhibit a method of construction of a determinant system for a product of arbitrary linear Fredholm operators acting between linear spaces. The method is based on tools of the determinant theory created by Leżański [1], developed and modified by Sikorski [2-4] and Buraczewski [5, 6].
We address the
problem of how to express a determinant system for product AB of
Fredholm operators ![]() and
and ![]() ,
X, Y, Z being linear spaces over the same field (real or
complex), in terms of determinant systems for A and B.
In the derivation of the main result we use some ideas presented in [7] for
Fredholm endomorphisms and extend them to Fredholm operators acting between
arbitrary linear spaces. Since the method proposed in the paper is purely
algebraic, we dispense with assumptions related to a topological structure of
linear spaces involved. The formulas, obtained as a direct and constructive
solution to the above mentioned problem, are generalizations of the classical
Cauchy-Binet formula
[8-10], which states that if A and B are two matrices over field F
of sizes
,
X, Y, Z being linear spaces over the same field (real or
complex), in terms of determinant systems for A and B.
In the derivation of the main result we use some ideas presented in [7] for
Fredholm endomorphisms and extend them to Fredholm operators acting between
arbitrary linear spaces. Since the method proposed in the paper is purely
algebraic, we dispense with assumptions related to a topological structure of
linear spaces involved. The formulas, obtained as a direct and constructive
solution to the above mentioned problem, are generalizations of the classical
Cauchy-Binet formula
[8-10], which states that if A and B are two matrices over field F
of sizes ![]() and
and ![]() ,
respectively, with
,
respectively, with ![]() , then
, then ![]() ,
where the sum is taken over all increasing sequences
,
where the sum is taken over all increasing sequences ![]() ,
with
,
with ![]() , and
, and ![]() (
(![]() ) is
) is ![]() submatrix
of A (B) obtained by deleting all columns (rows)
except these with indices in p. When
submatrix
of A (B) obtained by deleting all columns (rows)
except these with indices in p. When ![]() , the
formula becomes the well-known product formula
, the
formula becomes the well-known product formula ![]() for
determinants. The Cauchy-Binet formula plays an important role in studies of
determinants, permanents and other classes of matrix functions. An increasing
interest in its applications in many branches of applied science, such as
matrix analysis and engineering [11-13], is a motivation of the paper. It
is worth emphasizing that, so far, many considerable contributions to
generalizing the Cauchy-Binet theorem have been made [14-17]. In our approach,
the proposed generalization to Fredholm operators is based on the
correspondence between any Fredholm operator and its determinant system. We
also make use of analogues of the Laplace expansion formula that are available
for terms of determinant systems.
for
determinants. The Cauchy-Binet formula plays an important role in studies of
determinants, permanents and other classes of matrix functions. An increasing
interest in its applications in many branches of applied science, such as
matrix analysis and engineering [11-13], is a motivation of the paper. It
is worth emphasizing that, so far, many considerable contributions to
generalizing the Cauchy-Binet theorem have been made [14-17]. In our approach,
the proposed generalization to Fredholm operators is based on the
correspondence between any Fredholm operator and its determinant system. We
also make use of analogues of the Laplace expansion formula that are available
for terms of determinant systems.
2. Preliminaries
In this section we recall the main notions and facts concerning the determinant systems theory and we fix the notation [3-6, 18-20].
Suppose ![]() ,
, ![]() and
and ![]() are
pairs of conjugate linear spaces (over the real or complex field F) with
respect to scalar products I on
are
pairs of conjugate linear spaces (over the real or complex field F) with
respect to scalar products I on ![]() , J
on
, J
on ![]() and K on
and K on ![]() ,
respectively, satisfying the cancellation laws [6]. Elements
,
respectively, satisfying the cancellation laws [6]. Elements ![]() and
and ![]() are
called orthogonal if
are
called orthogonal if ![]() ; moreover,
; moreover, ![]() and
and ![]() for
given subsets
for
given subsets ![]() and
and ![]() .
Denote by
.
Denote by ![]() the value of
a
the value of
a ![]() -linear functional
-linear functional ![]() at a point
at a point ![]() .
.
D is said to be bi-skew symmetric if it is skew symmetric both
in variables ![]() and
and ![]() ;
; ![]() stands for the set of all bi-skew
symmetric functionals on
stands for the set of all bi-skew
symmetric functionals on ![]() . We call D an
. We call D an
![]() - functional on
- functional on ![]() if for arbitrary fixed elements
if for arbitrary fixed elements ![]() and
and ![]() there
exists an element
there
exists an element ![]() such that
such that ![]() for every
for every ![]()
![]() and for arbitrary fixed elements
and for arbitrary fixed elements ![]() ,
, ![]() there
exists an element
there
exists an element ![]() such that
such that ![]() for every
for every ![]()
![]() .
. ![]() is
identified with the set of all
is
identified with the set of all ![]() - functionals on
- functionals on ![]() . A bilinear
. A bilinear ![]() -
functional D on
-
functional D on ![]() is said to be an operator
on
is said to be an operator
on ![]() and
and ![]() stands
for its value at
stands
for its value at ![]() . We denote by
. We denote by ![]() the set of all
the set of all ![]() - operators on
- operators on ![]() . Each
. Each ![]() can
be simultaneously interpreted as a linear mapping
can
be simultaneously interpreted as a linear mapping ![]() and
as a linear mapping
and
as a linear mapping ![]() . Thus
. Thus ![]() for
for
![]() . The operator
. The operator ![]() ,
,
![]() ,
, ![]() being
fixed non-zero elements, defined by
being
fixed non-zero elements, defined by ![]() for
for ![]() , is called one-dimensional.
, is called one-dimensional.
For ![]() let
let
![]() ,
, ![]() ,
, ![]() ,
, ![]() . A
is said to be a Fredholm operator on
. A
is said to be a Fredholm operator on ![]() of order
of order
![]() and index
and index ![]() , if
, if
![]() ,
, ![]() ,
, ![]() and
and ![]() [5,
21]. An operator
[5,
21]. An operator ![]() satisfying
identities
satisfying
identities ![]() ,
, ![]() is called
a reflexive generalized inverse of
is called
a reflexive generalized inverse of ![]() [22].
A sequence
[22].
A sequence ![]() is said to be a determinant system
for A if
is said to be a determinant system
for A if ![]() , with
, with ![]() ,
, ![]()
![]() ,
, ![]() , and the generalized Laplace expansion
formulas hold
, and the generalized Laplace expansion
formulas hold
![]() ,
,
![]()
where ![]() ,
, ![]() ,
, ![]() . The least
. The least ![]() , such
that
, such
that ![]() , and the difference
, and the difference ![]() are called the order and the
index of
are called the order and the
index of ![]() , respectively.
, respectively.
As well-known [3, 5], an operator ![]() has a determinant system
has a determinant system ![]() if and only if A is Fredholm;
the orders (the indices) of A and
if and only if A is Fredholm;
the orders (the indices) of A and ![]() are
the same. Moreover, if A is Fredholm,
are
the same. Moreover, if A is Fredholm, ![]() is its reflexive generalized inverse and
is its reflexive generalized inverse and ![]() ,
,
![]()
![]() form complete systems of solutions of the homogenous equations
form complete systems of solutions of the homogenous equations ![]() and
and ![]() ,
respectively, then
,
respectively, then ![]() defined by the formula
defined by the formula
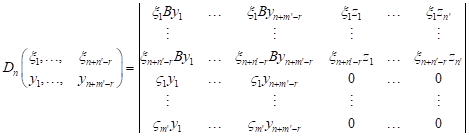 | (1) |
| for |
3. Main result
In this section we examine Fredholm operators acting from one linear space into another one. We provide a construction of a determinant system for a product of two fixed Fredholm operators. For the sake of completeness, we start by quoting some auxiliary results concerning reflexive generalized inverses of Fredholm operators, which are necessary for the proof of the main theorem of the paper.
In what follows, ![]() ,
, ![]() denote Fredholm operators of orders
denote Fredholm operators of orders ![]() ,
, ![]() and
indices
and
indices ![]() ,
,
![]() , respectively. Let
, respectively. Let ![]() ,
, ![]() ,
, ![]() and
and ![]() be
bases of
be
bases of ![]() ,
, ![]() ,
, ![]() and
and ![]() , respectively. The following direct sum decompositions hold:
, respectively. The following direct sum decompositions hold: ![]() ,
, ![]() being
subspaces such as
being
subspaces such as ![]() and
and ![]() .
Moreover, denoting
.
Moreover, denoting ![]() ,
, ![]() , we
also obtain
, we
also obtain ![]() , where
, where ![]() ,
, ![]() and
and
![]() . Let
. Let ![]() ,
,![]() be bases of subspaces
be bases of subspaces![]() ,
, ![]() , respectively, and
, respectively, and ![]() ,
, ![]() , where
, where ![]()
![]() ,
, ![]() being
the Kronecker symbol. Furthermore,
being
the Kronecker symbol. Furthermore,
![]() ,
, ![]() being
subspaces of dimensions
being
subspaces of dimensions ![]() ,
, ![]() , respectively.
, respectively.
Under the above given assumptions we recall [20] the following two results.
Lemma 3.1. If
![]() ,
, ![]() are arbitrary
reflexive generalized inverses of Fredholm operators
are arbitrary
reflexive generalized inverses of Fredholm operators ![]() ,
,![]() , respectively,
then
, respectively,
then ![]() and
and ![]() are bases of
are bases of ![]() and
and ![]() , respectively.
, respectively.
Lemma 3.2. We assume that:
(i) ![]() ,
, ![]() are
fixed determinant systems for Fredholm operators
are
fixed determinant systems for Fredholm operators
![]() ,
, ![]() , respectively;
, respectively;
(ii) ![]()
![]() are such elements that:
are such elements that:
![]() ;
;
(iii) ![]() ,
, ![]() are such elements
that:
are such elements
that:
![]() ;
;
(iv) ![]() is a
reflexive generalized inverse of
is a
reflexive generalized inverse of ![]() defined by the formula
defined by the formula
![]() for
for
![]() ; (2)
; (2)
(v) ![]() is a
reflexive generalized inverse of
is a
reflexive generalized inverse of ![]() defined by the formula
defined by the formula
![]() for
for
![]() . (3)
. (3)
Then
the operator ![]() is a reflexive generalized
inverse of
is a reflexive generalized
inverse of ![]() .
.
The following lemma plays an essential role in the sequel. It describes the connection between two arbitrary reflexive generalized inverses of a fixed Fredholm operator.
Lemma 3.3. If ![]() are
reflexive generalized inverses of a Fredholm operator
are
reflexive generalized inverses of a Fredholm operator ![]() and
and ![]() ,
, ![]() are bases of
are bases of ![]() ,
, ![]() , respectively, then there exist elements
, respectively, then there exist elements ![]()
![]() ,
, ![]()
![]() such
that
such
that
| (4) |
Proof. By the relationship between A and its reflexive generalized
inverse B [5], there exist elements ![]() ,
, ![]() such that
such that ![]()
![]() ,
, ![]()
![]() and the following identities hold:
and the following identities hold:
| (5) |
| Similarly, in view of the relationship between A and C, |
| (6) |
where ![]() ,
, ![]() are
elements satisfying conditions:
are
elements satisfying conditions:
![]()
![]() ,
, ![]()
![]() . By (5) and (6), bearing in mind
that
. By (5) and (6), bearing in mind
that ![]()
![]() ,
, ![]() . Consequently,
. Consequently, 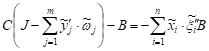 ,
which implies
,
which implies
| (7) |
| It follows from (7) that |
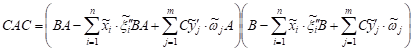 . . | (8) |
Since ![]()
![]() , we
transform the right-hand side of (8) into the form
, we
transform the right-hand side of (8) into the form
| (9) |
![]() .
.
| Furthermore, remembering that |
| (10) |
Hence, the identities ![]() ,
,
![]() , combined with (8) and (10), lead to
, combined with (8) and (10), lead to
| (11) |
Finally, by putting ![]()
![]() and
and ![]()
![]() in (11), we arrive at (4), which is the required result.
in (11), we arrive at (4), which is the required result.
Having established Lemmas 3.1-3.3, we are now in a position to state and prove the main result of the paper.
Theorem 3.4. Let ![]() ,
, ![]() be
fixed determinant systems for Fredholm
operators
be
fixed determinant systems for Fredholm
operators ![]() ,
,![]() , respectively.
If
, respectively.
If ![]() ,
, ![]() are arbitrary reflexive generalized
inverses of
are arbitrary reflexive generalized
inverses of ![]() ,
,![]() , respectively, then the sequence
, respectively, then the sequence ![]()
![]()
![]() defined by the formula:
defined by the formula:
| (12) |
| for |
![]() ,
, ![]() ,
,
| is a
determinant system for |
Proof. Let ![]() be reflexive generalized inverses of
be reflexive generalized inverses of ![]() ,
,![]() , respectively, defined
by formulas (2), (3). According to Lemma 3.2,
, respectively, defined
by formulas (2), (3). According to Lemma 3.2, ![]() is a reflexive generalized inverse of operator
is a reflexive generalized inverse of operator ![]() . It follows from (1), in view of Lemma
3.1, that the sequence
. It follows from (1), in view of Lemma
3.1, that the sequence ![]() defined by
defined by
| (13) |
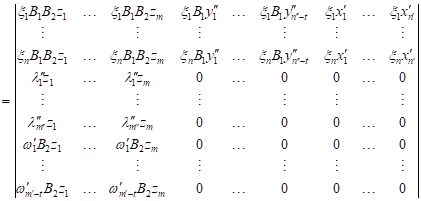 |
| (14) |
| where |
| (15) |
| for some |
| for some |
| Similarly, by (14), for any |
| Replacing |
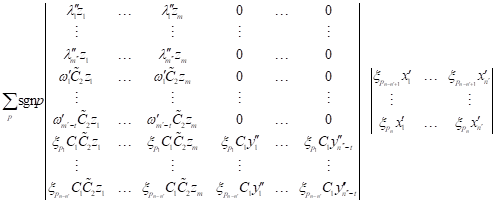 | (16) |
| multiplied by |
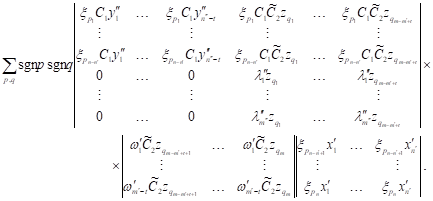 | (17) |
| Next, taking into
account the identities |
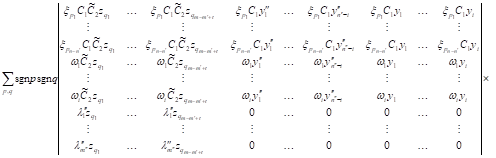 |
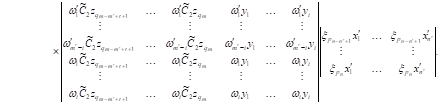 | (18) |
| It follows from
(18), bearing in mind the definition of |
| (19) |
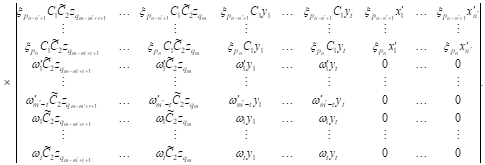 |
| By combining (18),
(19) with the relationship between |
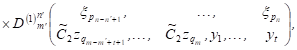 | (20) |
where ![]() or
or ![]() . In view of (14), Lemma 3.3 implies that
. In view of (14), Lemma 3.3 implies that
for some ![]() , is an
arbitrary reflexive generalized inverse of
, is an
arbitrary reflexive generalized inverse of ![]() . Bearing in mind the bi-skew symmetry of
. Bearing in mind the bi-skew symmetry of ![]() , we can substitute
, we can substitute ![]() for
for ![]() in (20).
Since a determinant system for the fixed Fredholm operator is determined up to
a constant (non-zero) factor, the sequence
in (20).
Since a determinant system for the fixed Fredholm operator is determined up to
a constant (non-zero) factor, the sequence ![]() defined
by (12) is
a determinant system for
defined
by (12) is
a determinant system for ![]() . This completes the
proof.
. This completes the
proof.
As a direct consequence of Theorem 3.4, we obtain the following result.
Corollary 3.5. Under the assumptions of Theorem 3.4, with ![]() , the formula (12) is of
Cauchy-Binet type.
, the formula (12) is of
Cauchy-Binet type.
4. Conclusions
In the paper, products of Fredholm operators acting between arbitrary linear spaces were considered. By exploiting terms of determinant systems for operators A and B, with AB well-defined, we provided a direct construction of a determinant system for AB. The obtained result leads to a generalization of the Cauchy-Binet formula to Fredholm operators and yields an important tool for solutions of problems in various branches of applied science and engineering.
References
[1] Leżański T., The Fredholm theory of linear equations in Banach spaces, Stud. Math. 1953, 13, 244-276.
[2] Sikorski R., On Leżański's determinants of linear equations in Banach spaces, Stud. Math. 1953, 14, 24-48.
[3] Sikorski R., Determinant systems, Stud. Math. 1959, 18, 161-186.
[4] Sikorski R., The determinant theory in Banach spaces, Colloq. Math. 1961, 8, 141-198.
[5] Buraczewski A., The determinant theory of generalized Fredholm operators, Studia Math. 1963, 22, 265-307.
[6] Buraczewski A., Sikorski R., Analytic formulae for determinant systems in Banach spaces, Studia Math. 1980, 67, 85-101.
[7] Buraczewski A., Determinant system for composite of generalized Fredholm operators, Studia Math. 1970, 34, 197-207.
[8] Marcus M., Minc H., Introduction to Linear Algebra, Dover Publications, New York 1988.
[9] Lancaster P., Tismenetsky M., The Theory of Matrices. Computer Science and Applied Mathematics, Academic Press, New York 1985.
[10] Shafarevich I.R., Remizov A.O., Linear Algebra and Geometry, Springer-Verlag, Berlin 2012.
[11] Brualdi R.A., Schneider H., Determinantal identities: Gauss, Schur, Cauchy, Sylvester, Kronecker, Jacobi, Binet, Laplace, Muir, and Cayley, Linear Algebra Appl. 1983, 52/53, 769-791.
[12] Vishwanathan S.V.N., Smola A.J., Vidal R., Binet-Cauchy kernels on dynamical systems and its application to the analysis of dynamic scenes, Int. J. Comput. Vision 2007, 73(1), 95-119.
[13] Konstantopoulos T., A multilinear algebra proof for the Cauchy-Binet formula and a multilinear version of Parseval’s identity, Linear Algebra Appl. 2013, 439 (9), 2651-2658.
[14] Karlin S., Rinott Y., A generalized Cauchy-Binet formula and applications to total positivity and majorization, J. Mult. Anal. 1988, 27, 284-299.
[15] Shevelev V., Combinatorial minors for matrix functions and their applications, Zeszyty Naukowe Politechniki Śląskiej 2014, seria: Matematyka Stosowana, 4, 5-16.
[16] Caracciolo S., Sokal A.D., Sportiello A., Noncommutative determinants, Cauchy-Binet formulae and Capelli-type identities. I. Generalizations of the Capelli and Turnbull identities, Electron. J. Comb. 2009, 16 (1), Research Paper R103, 1-43.
[17] Knill O., Cauchy-Binet for pseudo-determinants, Linear Algebra Appl. 2014, 459, 522-547.
[18] Ciecierska G., Determinant systems for nuclear perturbations of Fredholm operators in Frechet spaces, PanAmer. Math. J. 2014, 24(1), 1-20.
[19] Ciecierska G., Formulas of Fredholm type for Fredholm linear equations in Frechet spaces, Math. Aeterna 2015, 5(5), 945-960.
[20] Ciecierska G., Determinant systems method for computing reflexive generalized inverses of products of Fredholm operators, Math. Aeterna 2016, 6(6), 895-906.
[21] Ruston A.F., Fredholm theory in Banach spaces, Cambridge Tracts in Math. 86, Cambridge Univ. Press, Cambridge 1986.
[22] Ben-Israel A., Greville T.N.E., Generalized Inverses. Theory and Applications, Springer-Verlag, New York 2003.

