Image denoising using new wavelet thresholding function

IMAGE DENOISING USING NEW WAVELET THRESHOLDING FUNCTION

Bachir Dehda¹, Khaled Melkemi²

¹Department of Mathematics, University of Mohamed Khider
Biskra, Algeria
² Department of Mathematics, University of Elhadj Lakhdar
Batna, Algeria
dehda-bachir@univ-eloued.dz, kmelkemi@yahoo.fr

Received: 26 April 2017; accepted: 16 May 2017

Abstract. In this paper, we propose a new image denoising method based on wavelet thresholding. In this method, we introduce a new nonlinear thresholding function characterized by a shape parameter and basic properties. These characteristics make the new method able to achieve a compromise between both traditional thresholding techniques such as Hard and Soft thresholding. The experimental results show that our proposed method provides better performance compared to many classical thresholding methods in terms of the visual quality of the denoised image.

MSC 2010: 68U10, 94A08

Keywords: wavelet transform, image denoising, wavelet thresholding, wavelet shrinkage rules, peak signal to noise ratio (PSNR)

1. Introduction

Recovering an image that is corrupted by a noise during its acquisition or transmission is an open issue in the field of image processing and computer vision problems. Many researchers have been interested in noise reduction methods. These methods aim to recover the image in a way to be as close as possible to the original image. A vast number of papers about classical techniques in the spatial and transform domain has been published in literature [1]. Recently, the Multi-Diagonal Matrix Filter (MDMF) [2] and Lambda Multi-Diagonal Matrix Filter (Lambda-MDMF) [3] are proposed methods for image denoising at level of the spatial domain, which have given best performance compared to the Mean and Median filter [1]. At present, the most commonly used method for noise removal is the Discrete Wavelet Transform (DWT) [4, 5], which has given main contributions to image compression and denoising [6, 7]. In this approach, the thresholding of wavelet coefficients is a basic step in the denoising algorithm, where via a selected threshold value, only a small number of wavelet coefficients contain the necessary information of the image. Donoho and Johnstone [8] have proposed the hard and the soft thresholding techniques, that are the first and most widely used in image denoising with the Universal Threshold value (UT) [8]. In addition, the hard thresholding function is discontinuous and the soft thresholding function is continuous with a discontinuous derivative.

However, the thresholding techniques still suffer from the selection of the convenient threshold value. Then, the optimization methods as Stein's Unbiased Risk Estimate (SURE) [9] requires the second derivative of the thresholding function for obtaining an optimal threshold value. Further, Tang et al. [10] have considered that the differentiability of the thresholding function make the reconstructed signal more smoother.

For this purpose, in this paper, we propose a new class of a smooth nonlinear thresholding function based on the Gauss error function in its mathematical expression. This new thresholding function has high order derivatives into subintervals and characterized by a shape parameter, that can make it flexibly adjusted when we change the parameter value. Moreover, the simulation results have proved that the denoising using this new thresholding function has provided better performance compared to many other thresholding methods in terms of the visual quality of the denoised image.

This work is organized as follows: The next section recalls the principle of the wavelet denoising with an additive Gaussian noise. Section 3 introduces the classical thresholding methods and main shrinkage rule. Section 4 presents the new denoising method that is characterized by a new nonlinear thresholding function and describes the procedure of the proposed denoising method algorithm. Section 5 compares the simulation results of our proposed method with other thresholding methods.

Finally, we close this work by a conclusion and main references.

2. Noise reduction based on wavelet denoising

Let us consider an original image of size pixels, that will be recovered. Assume that is corrupted by an independent and an identically (i,i,d) zero mean white Gaussian noise with standard deviation . The observed noisy image will be given by this relation:

(1)

The goal of threshold denoising is to remove the noise from by estimating , which minimizes the mean square error (MSE) risk defined as:

(2)

Then, maximizes the Peak Signal to Noise Ratio (PSNR) in dB, that is written by:

(3)

In the wavelet domain, the Discrete Wavelet Transform (DWT) decomposes the noisy image into the following orthonormal bases at level :

(4)

where

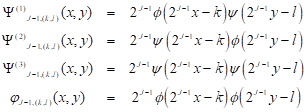and are respectively, the scaling and wavelet functions [5].

Then, the decomposition into , , and produces four subbands, are respectively LL, LH, HL and HH (see Fig. 1). The HH, HL and LH are called detail subbands and LL is called an approximation subband.

The wavelet thresholding denoising method processes each coefficient from the detail subbands with a thresholding function to obtain . Then, the denoised estimation image of the original image is the inverse discrete wavelet transform (IDWT) of , i.e, .

Fig. 1. Decomposition at level J = 1

3. Wavelet denoising using thresholding function

In the wavelet denoising, the way to perform denoising on images is by thresholding. The thresholding is a simple technique applied to wavelet coefficients using a thresholding function . The function should be characterized by a threshold value and two basic properties such as: Elimination of the small wavelet coefficients and reduction of the effect of large coefficients.

Donoho and Johnstone [8] have introduced two primary thresholding methods, which are Hard and Soft thresholding.

The Hard thresholding kills the wavelet coefficients, whose absolute values are lower than the threshold and keeps the other coefficients. The Hard thresholding function is expressed as follows:

(5)

The Soft thresholding kills the coefficients, whose absolute values are lower than the threshold and shrinks the nonzero coefficients towards zero. The soft thresholding function is defined as:

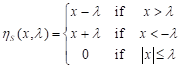(6)

Note that the Hard thresholding function is discontinuous at . Due to this discontinuity, this function yields artifacts in the denoised image. Whereas, the Soft thresholding function is continuous, so that the pseudo Gibbs phenomena can be avoided. But, when we reduce the coefficients by the threshold value, then in some cases the reconstructed image will be motivated by some deviations. Then, to overcome these drawbacks, Gao [11] considered the nonnegative Garrote thresholding function, which is continuous and shrinks or kills the coefficients. On the other hand, this thresholding function offers samples of advantages. The Garrote thresholding function is given by:

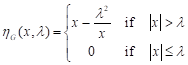(7)

and performs better than the two precedent thresholding techniques in terms of the visual quality of the denoised image.

In another side, the choice of a suitable threshold value is subject to shrinkage rules. Donoho and Johnstone [8] have proposed the Visu Shrink rule, where the threshold value is the Universal Threshold (UT) and defined as follows:

(8)

where is the noise variance and represents the size of the image. Moreover, the noise level can be estimated according to this formula [8]:

(9)

This method yields the best performance when the number of the pixels reaches infinity. Further, it can only deal with an additive Gaussian noise.

4. Presentation of the new denoising method

4.1. Proposed nonlinear thresholding function

The continuity in the Soft thresholding function is better property, but its first derivative is discontinuous and constant. So, in order to overcome the shortcom- ings of the Hard and the Soft thresholding functions, we propose an alternative thresholding function that verifies a compromise between both traditional thresh- olding functions. This new thresholding function is based on the Gauss Error Function in its mathematical expression and characterized by a shape parameter (). Its expression is given by the following formula:

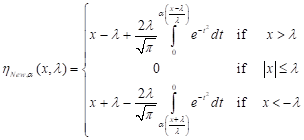(10)

This thresholding function is constructed for to be continuous and graphically located between the Hard and the Soft thresholding function.

From (10), we can conclude that: when , and when , . Then, the new thresholding function is continuous at the threshold point . If , , which can be seen that with increasing , becomes gradually close to , then has the same asymptotic convergence rate as the Hard and Soft thresholding function. Furthermore, the shape parameter can be adjusted freely such as, when , and when , (see Fig. 2).

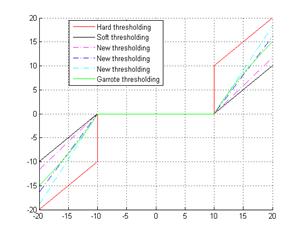Fig. 2. Graph of Hard, Soft, Garrote and Proposed thresholding with () respectively at

Moreover, this new thresholding function has the following properties:

Theorem 1. The New thresholding function is graphically located between the Hard and the Soft thresholding function.

Proof: We put for all ,

Then, is increasing function in the domain of and has the following properties:

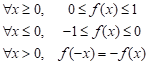Thus for we have

then, .

For then and

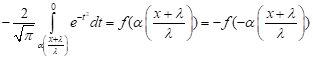This yields,

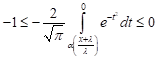Then,

For the functions , and are equal to zero.

Theorem 2. The New thresholding function is continuous in the domain of .

Proof: Since is continuous at , then is continuous everywhere.

Theorem 3. The New thresholding function is monotonous in the domain of .

Proof: For , we have

(11)

In another side, if , then

(12)

Since is continuous everywhere, then is monotonous in the domain of .

Theorem 4. The New thresholding function has high order derivatives into subintervals and .

Proof: From (11) and (12), we conclude that has high order derivatives into subintervals and .

Remark 1. Since has high order derivatives into subintervals, then the denoised image will be smooth.

Remark 2. In the literature, there are various optimization methods for determining an optimal shape parameter, whose Mean Square Error is as little as possible.

4.2. Proposed denoising method algorithm

In this subsection, we illustrate the basic steps concerning the procedure of the proposed denoising method algorithm with its flowchart (see Fig. 3).

Step 1. Load the noisy image.

Step 2. Apply the Discrete Wavelet Transform at level for the noisy image, then we get (LL, LH, HL, HH).

Step 3. Estimate the noise level using (9).

Step 4. Select the shrinkage rule applied to the proposed thresholding function.

Step 5. Take the Inverse Discrete Wavelet Transform to the thresholded components.

Step 6. Get the denoised image.

Fig. 3. Flowchart corresponding to the proposed method algorithm

5. Experimental results and discussion

In order to verify the effectiveness of our proposed denoising method, we compare it with the classical thresholding methods such as Hard, Soft and Garrote thresholding using the Visu Shrink rule. These thresholding methods are applied to various noisy test images of pixels, that are corrupted by a Gaussian noise with different noise levels (see Fig. 4). The wavelet that is used in all methods is the Haar wavelet in the decomposition level , where the optimal shape parameter is determined by a stochastic approximation method (Robbins- -Monro algorithm) [12]. So, the simulation results using Matlab are presented in Table 1.

Table 1

Comparison of PSNR (dB) results between the classical and proposed denoising methods

This Table presents the PSNR values corresponding to each image at different noise levels. The PSNR is a denoising criterion used to evaluate the quality of the denoised image, where the higher PSNR produces better denoising quality. Apparently, the experimental results show that at each noise level the PSNR that corresponds to our proposed method is the highest compared to all other methods for each image. Furthermore, the outperformance of the Garrote method for each image compared to the Hard and the Soft method appears at the high noise levels due to the selection of the threshold value. Whereas, our proposed method avoids this problem due to the existence of the shape parameter. Thus, our proposed denoising method outperforms all other denoising methods in terms of the visual quality of the denoised image (see Fig. 5).

Fig. 4. Original and corrupted images for Barbara with Gaussian noise level

Fig. 5. Denoised images, (a), (b), (c), (d) using Hard, Soft, Garrote and Proposed method respectively at Gaussian noise level

6. Conclusions

In this paper, we have developed a new image denoising method based on wavelet thresholding. In this new denoising method, the thresholding function is characterized by many mathematical properties, where our proposed method can overcome the shortcomings of the classical thresholding methods. The experimental results with many test images have shown the outperformance of our denoising method compared to Hard, Soft and Garrote thresholding methods in terms of the Peak Signal to Noise Ratio (PSNR), where our proposed method has given the highest PSNR.

References

[1] Rajni, Anutam, Image denoising techniques - an overview, International Journal of Computer Applications (0975-8887) 2014, 86, 16, January, 13-17.

[2] Anbarjafari G., Demirel H., Gokus A.E., A novel multi-diagonal matrix filter for binary image denoising, J. Adv. Electr. Comput. Eng. 2014, 1(1), 14-21.

[3] Li L., Ge H., Zhang Y., Low-density noise removal based on lambda multi-diagonal matrix filter for binary image, Neural Comput & Applic. 2016, DOI:10.1007/s00521-016-2538-7.

[4] Dehda B., Melkemi K., Novel method for reduction of wavelet coefficients number and its applications in images compression, IJAMML 2016, 5, 1, 43-65.

[5] Meyer Y., Wavelets and Operators, Cambridge Univ. Press, Cambridge 1992.

[6] En-Bing Lin, Yi Ling, Image compression and denoising via nonseparable wavelet approximation, Journal of Computational and Applied Mathematics 2003, 155, 131-152.

[7] Chang S.G. et al., Adaptive wavelet thresholding for image denoising and compression, IEEE Transactions on Image Processing 2000, 9, 9, September.

[8] Donoho D.L., Johnstone I.M., Adapting to unknown smoothness via wavelet shrinkage, J. Am. Statist. Assoc. 1995, 90, 1200-1224.

[9] Zhang X.-P. et al., Adaptive denoising based on sure risk, IEEE Signal Proessing Letters 1998, 5, 10, October.

[10] Tang J.-Y., Chen W.-T., Chen S.-Y., Zhou W., Wavelet-based vibration signal denoising with a new adaptive thresholding function, Journal of Vibration and Shock 2009, 28, 7, 118-121.

[11] Gao H.Y., Wavelet shrinkage denoising using the non-negative garrote, J. Comput. Graph. Statist. 1998, 7, 469-488.

[12] Kushner H.J., Yin G.G., Stochastic Approximation Algorithms and Applications, Application of Mathematics 1997, Vol. 35, Springer, 1997, DOI:10.1007/978-1-4899-2696-8. ISBN 978-1-4899-2698-2.

[13] Rahman T., Jianqiang Gao, Srinivas Nowduri, Segmentation of MRI images via mathematical morphology, IJAMML 2016, 5, 2, 115-121.