Response characteristics of non-uniform beam with time-dependent boundary conditions and under the actions of travelling distributed masses
Babatope Omolofe
,Alimi Adedowole
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
RESPONSE CHARACTERISTICS OF NON-UNIFORM BEAM WITH TIME-DEPENDENT BOUNDARY CONDITIONS AND UNDER THE ACTIONS OF TRAVELLING DISTRIBUTED MASSES
Babatope Omolofe1, Alimi Adedowole2
1Department
of Mathematical Sciences, School of Sciences
Federal University of Technology, PMB 704, Akure, Ondo State, Nigeria
2Department of Mathematical Sciences, Faculty of Sciences
Adekunle Ajasin University, Akungba-Akoko, Ondo State Nigeria
babatope_omolofe@yahoo.com, bomolofe@futa.edu.ng
Received: 20 April 2017; accepted: 26 June 2017
Abstract. In this paper, dynamic response of non-prismatic elastic beam resting on elastic foundation and subjected to moving distributed masses is investigated. To obtain the solution of the fourth order partial differential equations with singular and variable coefficients governing the motion of the structural member, an elegant mathematical procedure involving the Mindlin and Goodman's technique, the generalized Galerkin method and the asymptotic Struble's technique with the series representation of the Heaviside function. Various results obtained from the analysis of the closed form solutions are presented in plotted curves and fully discussed.
MSC 2010: 74H45,74K10
Keywords: resonance, time dependent, foundation modulus, distributed masses, uniform beam, Struble’s method, Galerkin equation, beam displacement
1. Introduction
The problem of assessing the dynamic response of a structural elements (beam or plate) which supports moving loads is fundamental in the analysis and design of high way and railway bridges and as such this problem continues to attract the attention of research engineers in the field of civil, mechanical, aerospace, transport engineering and related fields [1-16].
In most of the existing literatures on
dynamics of structures under moving loads, the vibration, analysis of elastic
beam with uniform cross-section under the passage of moving loads are commonly
investigated. In particular, both moments of inertia I and mass per unit
length ![]() of the beam are most often assumed not
varying with spartial coordinate
of the beam are most often assumed not
varying with spartial coordinate ![]() along the span
of the beam. In recent years, such important engineering problems as the
vibration of turbines, hulls of ships and bridge girders and so on, involving
the theory of vibration of structures of variable cross-section have
intensified the need for the study of the response of non-uniform elastic
systems under the action of moving loads.
along the span
of the beam. In recent years, such important engineering problems as the
vibration of turbines, hulls of ships and bridge girders and so on, involving
the theory of vibration of structures of variable cross-section have
intensified the need for the study of the response of non-uniform elastic
systems under the action of moving loads.
In most of the studies available in literature, see for example [17-30], the scope of the problem of assessing the dynamic response of a structural member under the passage of moving load has been limited to that of the beams with uniform cross section. Studies on the behaviour of non-prismatic elastic beam under the passage of moving load are not so common in literature. In few studies where non-uniform beam problems have been considered, the moving loads have been idealized as point-like. The problem of flexural vibration of non-uniform beam under moving loads was treated by Kolousek et al. [30]. They used normal-mode analysis to treat structure-load interaction problem. Much later, Oni and Omolofe, [31] investigated the dynamic behaviour of non-uniform Bernoulli-Euler beams subjected to concentrated loads travelling at varying velocities. In their study, they obtained analytical solution of the equation describing the motion and general behaviour of the vibrating system. Their result shows that for all variants of classical boundary conditions, the displacement of non-uniform Bernoulli-Euler beams subjected to concentrated loads travelling at varying velocities and transverse by moving masses decreases, as the values of both the foundation moduli and rotatory inertia correction factor increase. These works though impressive, the moving load involved in the governing equation of motions were model as concentrated load.
However, in engineering practice moving loads are most often in the form of distributed mass over a small segment of the entire length of the structural member as the traverse the structure rather than that of moving lumped mass [32, 33]. When the moving load is distributed, the problem of investigating the load-structure interactions becomes much more complicated. Thus, to study the dynamic characteristics of such dynamical systems to the degree of acceptable accuracy required and also for practical purposes, it is useful to consider elastic structural members subjected to moving distributed loads.
Thus, this work therefore concerns the problem of the dynamic response of non-uniform elastic having time dependent boundary conditions and under the action of moving distributed. Analytical procedures to obtain the solution of the governing equation will be developed and the effects of some vital structural parameters will be investigated.
2. Mathematical model formulation
Consider an elastic beam with a variable cross-section
resting on elastic subgrade and carrying a mass M as shown in Figure 1.
The beam properties such as the moment of inertia I, and the mass per
unit length of the beam ![]() vary along the span L. The
mass M is assumed to strike the non-uniform beam at t = 0 and
travels along it with a constant velocity type of motion. The flexural motion
of
this vibrating system, is governed by the fourth order partial differential
equation given as
vary along the span L. The
mass M is assumed to strike the non-uniform beam at t = 0 and
travels along it with a constant velocity type of motion. The flexural motion
of
this vibrating system, is governed by the fourth order partial differential
equation given as
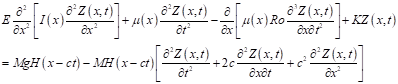 | (1) |
where: ![]() - the spatial is coordinate,
- the spatial is coordinate, ![]() is the time,
is the time, ![]() is the transverse displacement,
is the transverse displacement, ![]() is the variable flexural rigidity of the structure,
is the variable flexural rigidity of the structure, ![]() is the rotatory inertia correction factor,
is the rotatory inertia correction factor, ![]() is the foundation stiffness and
is the foundation stiffness and ![]() is the acceleration due to gravity, c is the constant
velocity of the motion.
is the acceleration due to gravity, c is the constant
velocity of the motion. ![]() and
and ![]() are variable moment of inertia and
beam mass per unit lenght respectively.
are variable moment of inertia and
beam mass per unit lenght respectively.
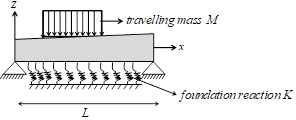
Fig. 1. Schematic diagram of non-uniform beam carrying uniformly distributed loads
Adopting the example in [6], ![]() and
and ![]() take
the forms,
take
the forms,
| (2) |
where ![]()
![]() and
and ![]() are
constants.
are
constants.
The boundary conditions of the above equation (1) are taken to be the time dependent, thus at each of the boundary points, there are two boundary conditions written as
| (3) |
where ![]() are
linear homogeneous differential operators of order less than or equal to three.
are
linear homogeneous differential operators of order less than or equal to three.
For instance, if the elastic beam is considered to be simply supported at both ends x = 0 and x = L then,
| (4) |
The initial conditions of the motion at ![]() are specified by two arbitrary
functions. Thus,
are specified by two arbitrary
functions. Thus,
| (5) |
Substituting equation (2) into equation (1), after some simplifications and rearrangements, leads to
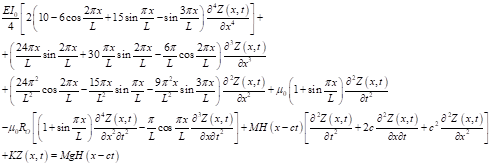 (6)
(6)
2.1. Operational simplification
The initial boundary value problem (6)
consisting of a non-homogeneous partial differential equation with a
non-homogeneous boundary conditions is transformed to a non-homogeneous partial
differential equation with a homogeneous boundary conditions, using the
Mindlin and Goodman [34]. In other to solve above initial boundary value
problem, we introduce the auxiliary variable ![]() in the form
in the form
| (7) |
Substituting equation (7) into the boundary
value problem (6), transforms the latter into a boundary value problem in terms
of ![]() . The displacement influence functions
. The displacement influence functions ![]() s are chosen so as to render the boundary
value problem in terms of
s are chosen so as to render the boundary
value problem in terms of ![]() homogeneous. Equation (6) in view
of equation (7) after some simplifications yields
homogeneous. Equation (6) in view
of equation (7) after some simplifications yields
![]()
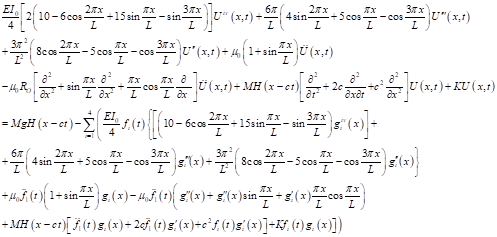
where over-dot represents the derivative with respect to time and the prime represents the derivative with respect to spacial coordinate. The expression in equation (7) must satisfy the boundary conditions in equation (3); consequently, we have
| (9) |
Substituting equation (7) into the initial conditions (5), one obtains
| (10) |
By Mindlin-Goodman method in [34], the
boundary condition (9) and (10) in terms of ![]() can
be made homogeneous if the functions
can
be made homogeneous if the functions ![]() s are chosen such that
sixteen conditions given by
s are chosen such that
sixteen conditions given by
| (11) |
| where | (12) |
is the Kronecker delta j, are satisfied.
Using equations (11) in the non-homogeneous boundary conditions (9) and (10) one obtains the homogeneous boundary conditions.
| (13) |
This dynamical system problem now reduces to that of solving the non-homogeneous partial differential equation (8) subject to the homogeneous boundary conditions in (13) with the non-homogeneous initial conditions (10).
3. Solution procedure
This section seeks to obtain the solution of the transformed fourth order partial differential equation having some coefficients which are not only variable but are also singular. A general approach is developed in order to solve the initial value problem. The approach involves the use of the technique called generalized Galerkin method and the expression of the Heaviside function as a Fourier sine series to transformed the governing equation of motion. The transformed equation is further simplified using a method called Struble’s asymptotic method.
The generalized Galerkin method requires that the solution of equation (8) be of the form
| (14) |
where ![]() is chosen such that the pertinent
boundary conditions are satisfied.
is chosen such that the pertinent
boundary conditions are satisfied.
Thus, substituting equation (14) into equation (8) after simplifications and rearrangements, leads to
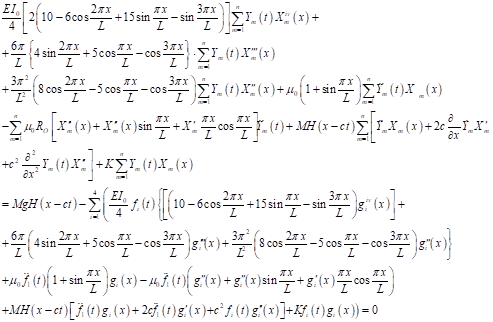 (15)
(15)
In order to determine ![]() ,
it is required that the expression on the left hand side of equation (15) be
orthogonal to function
,
it is required that the expression on the left hand side of equation (15) be
orthogonal to function![]() . Thus, multiplying equation (15)
by
. Thus, multiplying equation (15)
by ![]() and integrating from x = 0 to x
= L with respect to x, one obtains
and integrating from x = 0 to x
= L with respect to x, one obtains
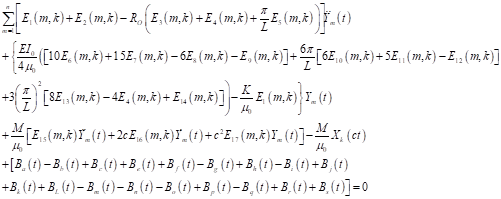 (16)
(16)
where ![]() , i
= 12…….16 are listed as follows:
, i
= 12…….16 are listed as follows:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (17)
(17)
Since our beam has simple support at both ends x = 0 and x = L, we therefore choose the function;
| (18) |
and the frequency equations as
| (19) |
Expressing the Heaviside function in Fourier sine series thus gives,
| (20) |
4. Solutions of the transformed governing equations
This section seeks the solution to the transformed equation (16).
Substituting equations (18), (19) and (20) into equation (16) and after some simplifications and rearrangements yields.
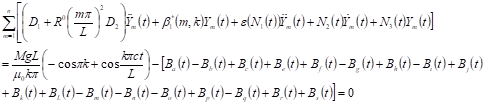 (21)
(21)
where:
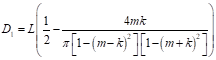 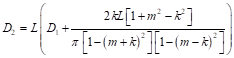 | (22) |
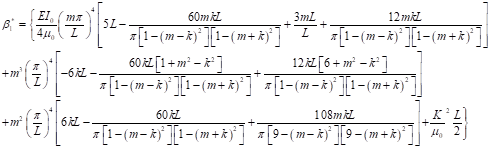 (23)
(23)
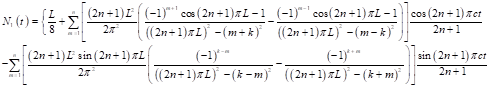 (24)
(24)
![]()
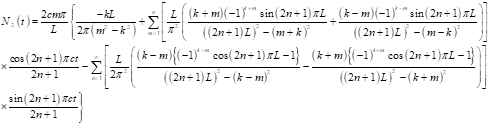
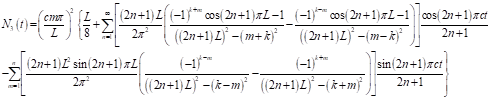 (26)
(26)
At this juncture, it is pertinent to obtain
the particular ![]() that ensure zeros of the
right hand sides of the boundary conditions for simply supported beam. In view
of equations (11), the
that ensure zeros of the
right hand sides of the boundary conditions for simply supported beam. In view
of equations (11), the ![]() are obtained for simply supported elastic beam with time
dependent boundary conditions as,
are obtained for simply supported elastic beam with time
dependent boundary conditions as,
| (27) |
it is only necessary to compute
those ![]() for which the corresponding
for which the corresponding ![]() do not vanish. Thus, we need only
do not vanish. Thus, we need only ![]() and
and ![]() for
our boundary displacement functions
for
our boundary displacement functions ![]() and
and ![]() . In view of equations (27) above
. In view of equations (27) above
| (28) |
while,
| (29) |
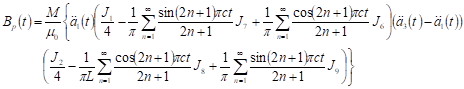 | (30) |
| (31) |
| where: |
| (32) |
Substituting equation (28) to (31) into equation (21) after some rearrangements and simplifications, one obtains,
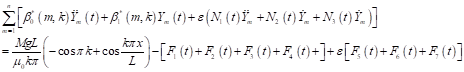 | (33) |
where:
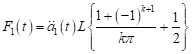 | (34) |
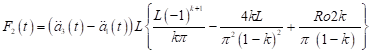
| (35) |
| (36) |
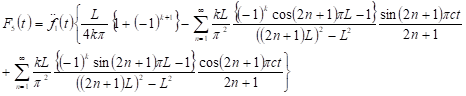 | (37) |
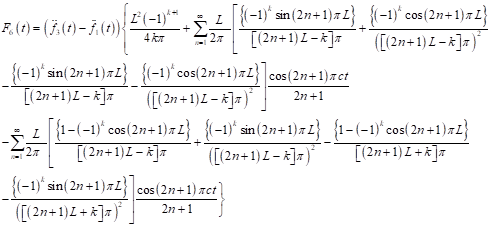 |
| (39) |
Equation (33) represents the transformed equation of the non-uniform elastic beam simply-supported at both ends and having boundary and initial conditions which is time dependent. In what follows, we shall discuss two special cases of the equation (33) namely; the moving force and the moving mass problems.
4.1. The moving force load-beam interaction problem
By setting ![]() in equation (33), an approximate model of the governing
differential equation describing the response of a non-uniform, elastic beam
traversed by a moving force would be obtained.
in equation (33), an approximate model of the governing
differential equation describing the response of a non-uniform, elastic beam
traversed by a moving force would be obtained.
Thus, setting ![]() in
equation (33), yields
in
equation (33), yields
| (40) |
where,
| (41) |
Now, one considers a beam whose end ![]() , (say) is subjected to a sine-wave
(undamped) transient displacement, starting from rest and the other end
, (say) is subjected to a sine-wave
(undamped) transient displacement, starting from rest and the other end ![]() , is subjected to a damped sine wave
transient displacement starting from rest. Thus,
, is subjected to a damped sine wave
transient displacement starting from rest. Thus,
| (42) |
where A, B are
amplitudes,![]() is the frequency and
is the frequency and ![]() is a parameter. Substituting
is a parameter. Substituting ![]() ,
, ![]()
![]() and
and ![]() in
the initial conditions (5), one obtains
in
the initial conditions (5), one obtains
| (43) |
When equations (42) and (43) are substituted into (40) after simplifications and rearrangements, one obtains
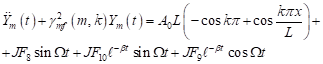 | (44) |
where,
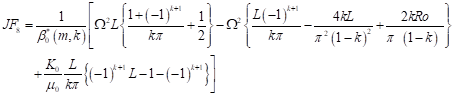 | (45) |
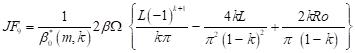 | (46) |
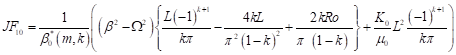 | (47) |
Using the integral transformation technique to treat (47) in conjunction with the initial conditions (5) gives,
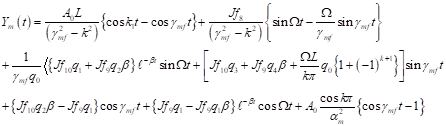 | (48) |
which when substituted into equation (14) gives
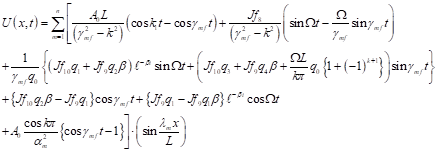 | (49) |
where
But from equation (7) we have
| (51) |
Consequently,
| (52) |
Equation (52) represents the dynamic response to moving distributed forces of non-uniform elastic beam whose two simply-supported edges undergo displacements which vary with time.
4.2. The moving mass load-beam interaction problem
If the mass of the moving load is commensurable
with that of the structure the inertia effect of the moving mass is considered
not negligible. In this case, ![]() and the solution to
the entire equation (33) is required. Thus, we resort to the
asymptotic Struble method of extensively discussed in [5, 7]. To this effect,
equation (33) is rearranged to take the form,
and the solution to
the entire equation (33) is required. Thus, we resort to the
asymptotic Struble method of extensively discussed in [5, 7]. To this effect,
equation (33) is rearranged to take the form,
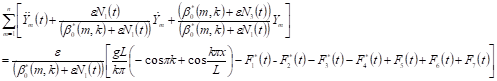 | (53) |
where
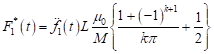 , , 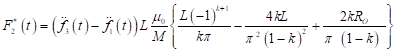
| (54) |
and ![]() ,
,![]() ,
,![]() are as defined in equations (37), (38)
and (39).
are as defined in equations (37), (38)
and (39).
By Struble technique, the LHS of equation (53) is simplified to take the form
| (55) |
where
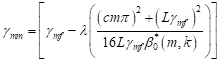 | (56) |
is called the modified natural frequency representing the frequency of the free system due to the presence of the moving mass, thus, in view of equation (55), equation (53) becomes,
![]() (57)
(57)
Solving equation (57) above again using
integral transformation technique in conjunction with initial conditions (5),
the expression for ![]() is obtained and substituted
into (14) and consequently, one obtains
is obtained and substituted
into (14) and consequently, one obtains
| (58) |
Equation (58) represents the dynamic response to moving distributed masses of the non-uniform beam whose two simply-supported edges undergo displacements which vary with time.
5. Discussion of the analytical solutions
Occurrence of a resonance phenomenon is investigated in this section. Equation (52) clearly shows that the simply supported elastic beams transverse by a moving force will be in state of resonance whenever
| (59) |
While equation (58) shows that the same beam under the action of moving mass experiences resonance effect when
| (60) |
From equation (56)
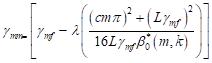 | (61) |
This implies
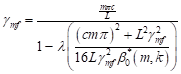 | (62) |
Evidently, from (59) and (61), for the same natural frequency, the critical speed for the system consisting of a simply supported elastic beam on a Winkler foundation and traverse by moving distributed force with uniform speed is greater than that of moving distributed mass problem. Thus, resonance is reached earlier in the moving mass system than in the moving force system.
6. Numerical calculations and discussion of results
In order to
illustrate the foregoing analysis and results obtained for the dynamical system
in discussion, a simply supported non-uniform beam of length
L = 12.192 m is considered. It is assumed that the mass travels at the
constant
velocity c = 8.123 m/s. Furthermore, the value for E is chosen to
be 2.109x109 kg/m2. For various values of the
foundation moduli K, and the rotatory inertia correction factor ![]() , the deflections of the simply
supported beam are calculated and plotted against time t.
, the deflections of the simply
supported beam are calculated and plotted against time t.
Figures 2 and 5
display the effect of rotatory inertia correction factor ![]() on the transverse deflection of the
simply supported beam in both cases of moving force and moving mass
respectively. The graphs show that the response amplitude decreases as the
values of the rotatory inertia increases for fixed values of the foundation
moduli K = 4 000 000 N/m3.
on the transverse deflection of the
simply supported beam in both cases of moving force and moving mass
respectively. The graphs show that the response amplitude decreases as the
values of the rotatory inertia increases for fixed values of the foundation
moduli K = 4 000 000 N/m3.
Also, Figures 3
and 6 show the deflection profile of the simply supported beam for moving force
and moving mass respectively for various values foundation modulus K and
for fixed value of ![]() . It is shown from the figures that as
the values of K increases the deflection of the beam decreases. Figure 4
displays the transverse displacement response of a simply
supported non-uniform beam with time dependent boundary
conditions under the action of distributed forces for various values of
position coordinates x and for fixed values of foundation modulus
K = 4 000 000 and rotatory inertia correction factor Ro = 5.
The figure shows that as position coordinates X increases, the dynamic
deflection of the non-uniform beam increases.
. It is shown from the figures that as
the values of K increases the deflection of the beam decreases. Figure 4
displays the transverse displacement response of a simply
supported non-uniform beam with time dependent boundary
conditions under the action of distributed forces for various values of
position coordinates x and for fixed values of foundation modulus
K = 4 000 000 and rotatory inertia correction factor Ro = 5.
The figure shows that as position coordinates X increases, the dynamic
deflection of the non-uniform beam increases.
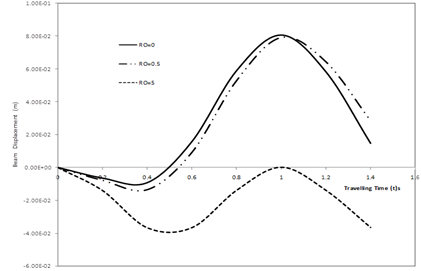
Fig. 2. Deflection profile of a non-uniform simply supported elastic beam to moving force for different values of rotatory inertia Ro fixed values of foundation modulus K = 4 000 000
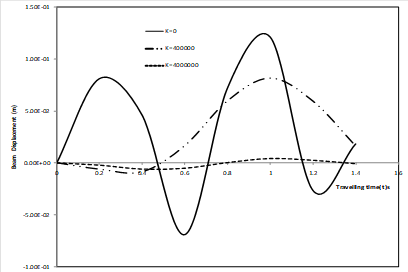
Fig. 3. Transverse displacement response of simply supported non-uniform elastic beam under a moving force for various values of foundation moduli K and fixed value rotatory inertia Ro = 4
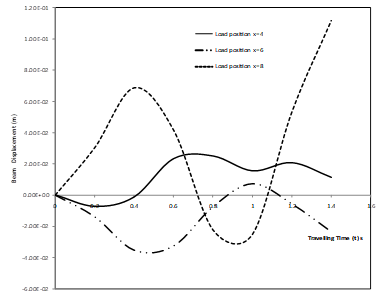
Fig. 4. Deflection profile of a non-uniform simply supported elastic beam under moving force for various values of load position x
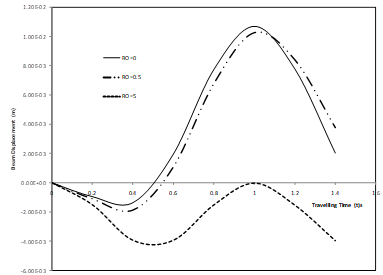
Fig. 5. Transverse displacement response of simply supported non-uniform elastic beam under a moving mass for various values of rotary inertia Ro and fixed value of foundation moduli K = 4 000 000
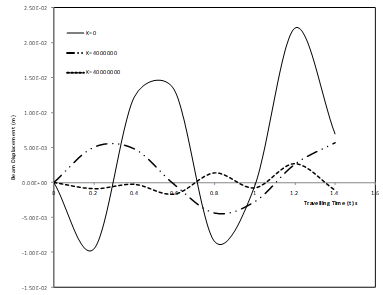
Fig. 6. Transverse displacement response of simply supported non-uniform elastic beam under a moving mass for various values of foundation moduli K and fixed value rotatory inertia Ro = 4
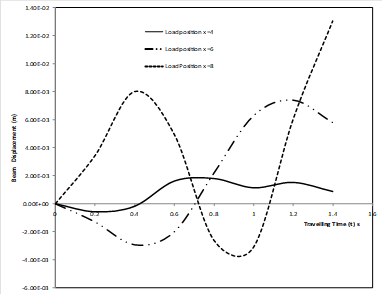
Fig. 7. Deflection profile of a non-uniform simply supported elastic beam under moving mass for various values of load position x
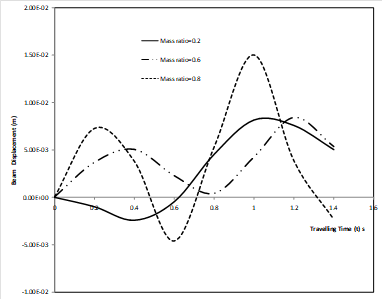
Fig. 8. Deflection profile of a non-uniform simply supported elastic beam under moving mass for various values of the mass ratio
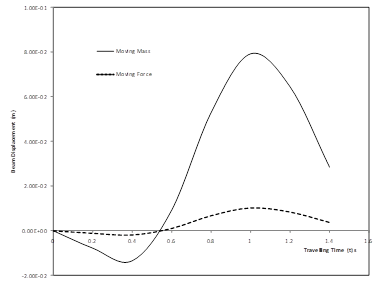
Fig. 9. Comparison of the deflection profiles of the moving force and moving mass models for fixed values of foundation moduli K = 4 000 000 and rotatory inertia Ro = 4
Similarly, Figure 7 displays the transverse displacement response of a simply supported non-uniform elastic beam with time dependent boundary conditions under the action of distributed masses for various values of position coordinates and for fixed values of foundation modulus K = 4 000 000 and rotatory inertia correction factor Ro = 5. The result shows that as position coordinates x increases, the dynamic deflection of the non-uniform beam increases. For various traveling time t, the deflection profile of the beam for various values of mass ratio and for fixed values of foundation modulus K = 4 000 000 and rotatory inertia correction factor Ro = 5 are shown in Figure 8. It is observed that as the mass ratio increases the deflection of the vibrating beam increases. Figure 9 compares the displacement curves of the moving force and moving mass for a simply supported beam with foundation modulus K = 4 000 000 N/m3 and rotatory inertia correction factor Ro = 5.
7. Concluding remarks
The problem of transverse motion of a non-uniform beam with time-dependent boundary conditions when under the actions of travelling distributed masses has been scrutinized. The Mindlin and Goodman’s technique is first applied to transform the governing non-homogeneous fourth order partial differential equations with non-homogeneous boundary conditions into non-homogeneous fourth order partial differential equations with homogeneous boundary conditions. The resultant transformed equation is further treated using the versatile the generalised Galerkin method with the series representation of the Heaviside function and a modification of asymptotic Struble method. Analytical solutions of the governing fourth order partial differential equations with variable and singular coefficients of the structure-mass interaction problem are presented. Illustrative example involving a variable cross-section slender member with simple supports at both ends is presented. The solutions hitherto obtained are analyzed and resonance conditions for this dynamical beam-mass system are established. It is found that as the values of foundation subgrade K increases the deflection of the beam decreases. This is also true for all other beam parameters used in this work. The higher the value of the mass ratio, the larger the deflection of the beam. This is also true of the load position. Various results obtained in this study are in perfect agreement with existing results in literatures are quite useful in design engineering and other related fields.
Nomenclature
E [N/m2] Modulus of elasticity
![]() [kg/m] Beam
Variable Mass per unit length
[kg/m] Beam
Variable Mass per unit length
Ro [m] Rotatory inertia correction factor
M [kg] Mass of the moving load
![]() Displacement
influence function
Displacement
influence function
![]() Differential
operator
Differential
operator
![]() [m] Unknown
function of time
[m] Unknown
function of time
L [m] Length of the beam
![]() Modified
natural frequency
Modified
natural frequency
![]() [m4] Variable
moment of inertia
[m4] Variable
moment of inertia
Z(x,t) [m] Beam displacement
K [N/m3] Foundation stiffeness
C [m/s] Speed of the moving load
![]() Kronecker
delta
Kronecker
delta
![]() Beam
modes
Beam
modes
![]() [m/s2] Acceleration
due to gravity
[m/s2] Acceleration
due to gravity
![]() [Hz] Natural
frequency
[Hz] Natural
frequency
![]() Normalized deflection curves for the ith
mode of the vibrating beam
Normalized deflection curves for the ith
mode of the vibrating beam
References
[1] Timoshenko S., Young D.H., Weaver W., Vibration Problems in Engineering, 4th John Wiley Edition, New York 1964.
[2] Fryba L., Vibrations of Solids and Structures under Moving Loads, Groningen, Noordhoff 1972.
[3] Milormir M., Stanisic M.M., Hardin J.C., On the response of beams to an arbitrary number of concentrated moving masses, Journal of the Franklin Institute 1969, 287(2), 115-123.
[4] Sadiku S., Leipholz H.H.E., On the dynamics of elastic systems with moving concentrated masses, Ing. Archiv. 1981, 57, 223-242.
[5] Gbadeyan J.A., Oni S.T., Dynamic behaviour of beams and rectangular plates under moving loads, Journal of Sound and Vibration 1995, 182(5), 677-695.
[6] Kargarmovin M.H., Younesian D., Dynamics of Timoshenko beams on Pasternak foundation under moving load, Mechanics Research Communications 2004, 31, 713-723.
[7] Awodola T.O., Oni S.T., Dynamic behaviour under moving concentrated masses of simply supported rectangular plates resting on variable Winkler elastic foundation, Latin America Journal of Solid and Structures 2011, 8(4), 373-392.
[8] Ali R.D., Mahdi B., Hassan G., Mesbah S., Boundary Element Method applied to the bending analysis of thin functionally graded plates, Latin America Journal of Solid and Structures 2013, 10(3), 549-570.
[9] Shahin N.A., Mbakisya O., Simply supported beam response on elastic foundation carrying repeated rolling concentrated loads, Journal of Engineering Science and Technology 2010, 5(1), 52-66.
[10] Ghugal Y.M., Sayyad A.S., Free vibration of thick orthotropic plates using trigonometric shear deformation theory, Latin America Journal of solid and structure 2011, 8, 229-243.
[11] Zolkiewski S., Vibrations of beams with a variable cross-section fixed on rotational rigid disks, Latin American Journal of Solids and Structures 2013, 10, 39-57.
[12] Hsu J.C., Lai H.Y., Chen C.K., Free vibration of non-uniform Euler-Bernoulli beams with general elastically end constraints using Adomian modified decomposition method, Journal of Sound and Vibration 2008, 318, 965-981.
[13] Saravi M., Hermaan M., Ebarahimi K.H., The comparison of homotopy perturbation method with finite difference method for determination of maximum beam deflection, Journal of Theoretical and Applied Physics 2013, 7, 8.
[14] Li R., Zhong Y., Li M.L., Analytic bending solutions of free rectangular thin plates resting on elastic foundations by a new symplectic superposition method, Proceedings of the Royal Society A 2013, 46, 468-474.
[15] Nikkhoo A., Rofooei F.R., Parametric study of the dynamic response of thin rectangular plates traversed by a moving mass, Acta Mechanica 2012, 223(1), 15-27.
[16] Zarfam R., Khaloo A.R., Nikkhoo A., On the response spectrum of Euler-Bernoulli beams with a moving mass and horizontal support excitation, Mechanics Research Communications 2013, 47, 77-83.
[17] Stanisic M.M., Hardin J.C., Lou Y.C., On the response of the plate to a multi-masses moving system, Acta Mechanical 1968, 5, 37-53.
[18] Oni S.T., Adedowole A., Influence of prestress on the response to moving loads of rectangular plates incorporating rotatory inertia correction factor, Journal of the Nigerian Association of Mathematical Physics 2008, 13, 127-140.
[19] Oni S.T., On the dynamic response of elastic structures to moving multi-mass systems, PhD Thesis, University of Ilorin, Ilorin, Nigeria 1991.
[20] Oni S.T., Awodola T.O., Dynamic response to moving concentrated masses of uniform Rayleigh beams resting on variable Winkler elastic foundation, Journal of the Nigerian Association of Mathematical Physics 2005, 9, 151-162.
[21] Omer C., Aitung Y., Large deflection static analysis of rectangular plates on two parameter elastic foundations, International Journal of Science and Technology 2005, 1(1), 43-50.
[22] Adams G.G., Critical speed and the response of a tensioned beam on an elastic foundation to repetitive moving loads, International Journal of Mechanical Sciences 1995, 7, 773-781.
[23] Savin E., Dynamics amplification factor and response spectrum for the evaluation of Vibrations of beams under successive moving loads, Journal of Sound and vibrations 2001, 248(2), 267- -288.
[24] Jia-Jang W., Vibration analysis of a portal frame under the action of a moving distributed mass using moving element, International Journal for Numerical Methods in Engineering 2006, 66, 2028-2052.
[25] Kenny J., Steady state vibrations of a beam on an elastic foundation for a moving load, Journal of Applied Mechanics 1954, 76, 359-364.
[26] Shahidi M., Bayat M., Pakar I., Abdollahzadeh G., On the solution of free non-linear vibration of beams, International Journal of Physical Science 2011, 6(7), 1628-1634.
[27] Zolkiewski S., Damped vibrations problem of beams fixed on the rotational disk, International Journal of Bifurcation and Chaos 2011, 21(10), 3033-3041.
[28] Zolkiewski S., Numerical application for dynamical analysis of rod and beam systems in transportation, Solid State Phenomena 2010, 164, 343-348.
[29] Zarfam R., Khaloo A.R., Nikkhoo A., On the response spectrum of Euler-Bernoulli beams with a moving mass and horizontal support excitation, Mechanics Research Communications 2013, 47, 77-83.
[30] Kolousek V., Civil Engeering Structures subjected to Dynamic Loads, SVTL, Bratislava (in Slovak) 1967.
[31] Oni S.T., Omolofe B., Dynamic behaviour of non-uniform bernoulli-euler beams subjected to concentrated loads travelling at varying velocities, Journal of the Nigerian Association of Mathematical Physics 2005, 9, 79-102.
[32] Ogunyebi S.N., Dynamical analysis of finite prestressed Bernoulli-Euler beam with general boundary conditions under travelling distributed loads, M.Sc. Dissertation, Federal University of Technology, Akure, Nigeria, 2006.
[33] Oni S.T., Ogunyebi S.N., Dynamical analysis of a prestressed elastic beam with general boundary conditions under the action of uniform distributed masses, Journal of the Nigerian Association of Mathematical Physics 2008, 12, 87-102.
[34] Mindlin R.D., Goodman L.E., Beam vibration with time-dependent boundary condition, J. Appl. Mech. 1950, 17, 377-380.

