The fundamental solutions to the central symmetric time-fractional heat conduction equation with heat absorption
Yuriy Povstenko
,Joanna Klekot
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE FUNDAMENTAL SOLUTIONS TO THE CENTRAL SYMMETRIC TIME-FRACTIONAL HEAT CONDUCTION EQUATION WITH HEAT ABSORPTION
Yuriy Povstenko1, Joanna Klekot 2
1Institute
of Mathematics and Computer Science, Faculty of Mathematical and Natural
Sciences, Jan Długosz University in Częstochowa
Częstochowa, Poland
2Institute of Mathematics, Częstochowa University of Technology
Czestochowa, Poland
j.povstenko@ajd.czest.pl, joanna.klekot@im.pcz.pl
Received: 8 March 2017; accepted: 12 June 2017
Abstract. The time-fractional heat conduction equation with heat absorption proportional to temperature is considered in the case of central symmetry. The fundamental solutions to the Cauchy problem and to the source problem are obtained using the integral transform technique. The numerical results are presented graphically.
MSC 2010: 35K05, 35R11, 26A33, 44A10, 42A38
Keywords: non-Fourier heat conduction, Caputo fractional derivative, heat absorption, Laplace integral transform, Fourier transform, Mittag-Leffler function
1. Introduction
The classical heat conduction is based on the standard Fourier law and the parabolic heat conduction equation. The time-nonlocal dependence of the heat flux and the temperature gradient with the “long-tail” power kernel [1-4] can be interpreted in terms of fractional integrals and derivatives and results in the time-fractional heat conduction equation
| (1) |
where T is a temperature, t denotes time, Δ stands for the Laplace operator, a is an analogue of the thermal diffusivity coefficient. The Caputo fractional derivative is defined as [5-7]
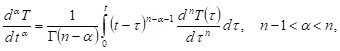 | (2) |
with ![]() being the gamma
function.
being the gamma
function.
Fractional calculus (the theory of integrals and derivatives of non-integer order) provides the appropriate mathematical tool for description of many phenomena in physics, chemistry, biology, and engineering [8-15].
If volume heat absorption proportional to temperature occurs in a body, then instead of (1) we get
| (3) |
where the values of the coefficient b > 0 and b < 0 correspond to heat absorption and heat release, respectively. The classical heat conduction equation with the additional term proportional to temperature was considered in [16-18]. Similar equations appear in the theory of bio-heat transfer [19] and in the survival probability [20]. Mathematical and physical aspects of fractional heat conduction equation with heat absorption were studied in the literature in the case of one Cartesian coordinate in [21-24]. In the present paper, we study the fundamental solutions to the Cauchy problem and to the source problem for equation (3) in spherical coordinates in the case of central symmetry. The obtained solutions generalize the results of the paper [25], where the case b = 0 was considered.
2. The fundamental solution to the Cauchy problem
We consider the time-fractional heat conduction equation with one spatial variable in spherical coordinate system
| (4) |
where
![]()
Equation (4) is considered under initial conditions
| (5) |
| (6) |
with ![]() being the Dirac delta
function. For the sake of convenience and to obtain the nondimensional
quantities used in calculations, we have introduced the constant multiplier
being the Dirac delta
function. For the sake of convenience and to obtain the nondimensional
quantities used in calculations, we have introduced the constant multiplier ![]() in equation (5).
in equation (5).
The zero condition at infinity is also imposed:
| (7) |
To solve the Cauchy problem under
consideration we use the integral transform technique. The Laplace transform
with respect to the time ![]() is defined as
is defined as
| (8) |
with the inverse carried out according to the Fourier-Mellin formula
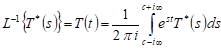 , , | (9) |
where s denotes
the transform variable, ![]() is a positive fixed number such that all the singularities of
is a positive fixed number such that all the singularities of ![]() lie to the left of the
vertical line
lie to the left of the
vertical line ![]() .
.
For the Laplace transform rule, the Caputo
fractional derivative requires
the knowledge of the initial values of the function and its integer derivatives
of the order ![]()
| (10) |
Applying the Laplace transform to equation (4) and taking into account the rule (10) with the initial conditions (5) and (6) gives
![]() . (11)
. (11)
Next, we use the
Fourier transform with respect to the spatial coordinate ![]() in the case of spherical symmetry [4,
26]:
in the case of spherical symmetry [4,
26]:
| (12) |
| (13) |
| (14) |
Usually the Fourier transform (12)-(13) is used under the assumption of boundedness of T(r) at the origin (see, e.g., [18]); sometimes this assumption is substituted by less restrictive condition prescribing a type of singularity of the function at r = 0 (see, for instance, [27]).
Application of the Fourier transform (12) and formula (14) to equation (11) leads to
| (15) |
Inversion of the integral transforms results in the solution:
| (16) |
where ![]() is the Mittag-Leffler function in one
parameter
is the Mittag-Leffler function in one
parameter ![]() [5-7]
[5-7]
| (17) |
and the following formula has been used:
| (18) |
Using the nondimensional quantities
| (19) |
one obtains the following solution:
| (20) |
For ![]() the Mittag-Leffler function
the Mittag-Leffler function ![]() , and from (20) we get
, and from (20) we get
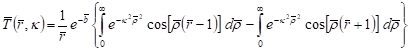 . . | (21) |
Taking into account that [28]
| (22) |
we arrive at the solution
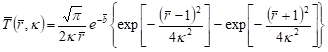 . . | (23) |
In the particular case ![]() , the Mittag-Leffler function
, the Mittag-Leffler function ![]() can be
represented as [4]
can be
represented as [4]
| (24) |
and the solution has the following form
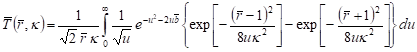 . . | (25) |
The results of
numerical calculations for ![]() , different values of
, different values of ![]() and the order of the time-fractional derivative
and the order of the time-fractional derivative ![]() are shown in
Figures 1-5.
are shown in
Figures 1-5.
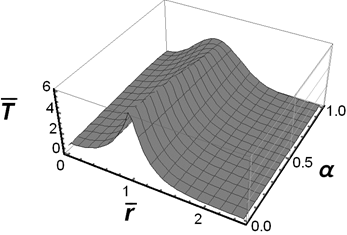 |
Fig. 1. The fundamental solution to the
Cauchy problem for ![]() and
and ![]()
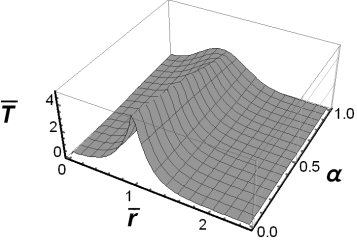
Fig. 2. The fundamental solution to the
Cauchy problem for ![]() and
and ![]()
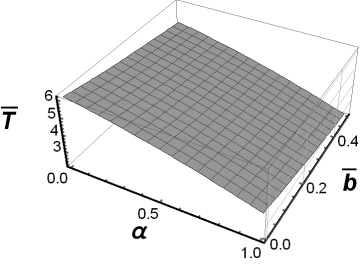
Fig. 3. The fundamental solution to the
Cauchy problem for ![]() ,
,![]() and
and ![]()
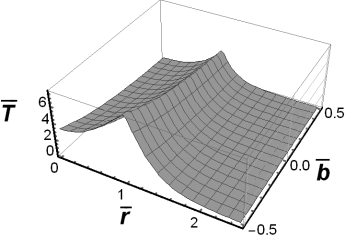
Fig. 4. The fundamental solution to the
Cauchy problem for ![]() and
and ![]()
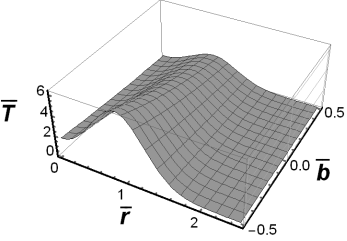
Fig. 5. The fundamental solution to the
Cauchy problem for ![]() and
and ![]()
3. The fundamental solution to the source problem
Consider the time-fractional heat conduction equation with the source term
![]() (26)
(26)
under zero initial conditions
| (27) |
| (28) |
Using the integral transforms technique, we obtain
| (29) |
As
| (30) |
where ![]() is the Mittag-Leffler function in two
parameters
is the Mittag-Leffler function in two
parameters ![]() and
and ![]() [5-7]
[5-7]
| (31) |
the inverse transforms applied to equation (29) lead to
| (32) |
and
| (33) |
In this case, the nondimensional temperature is introduced as
| (34) |
and other nondimensional quantities are the same as in (19).
In the case ![]() [4]
[4]
| (35) |
Taking into account (35), (38) and (25), we arrive at
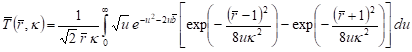 . (36)
. (36)
Figures 6-8 show the results of numerical
calculations according to equations (33) and (36) for ![]() .
.
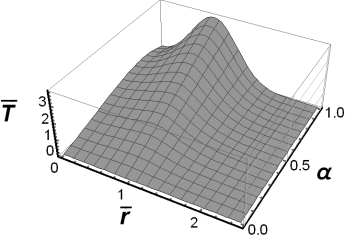
Fig. 6. The fundamental solution to the
source problem for ![]() and
and ![]()
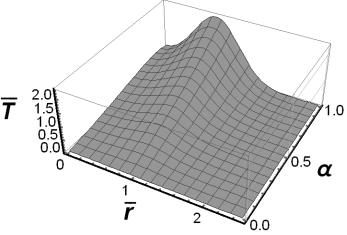
Fig. 7. The fundamental solution to the
source problem for ![]() and
and ![]()
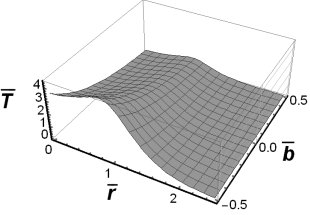
Fig. 8. The fundamental solution to the
source problem for ![]() and
and ![]()
4. Conclusions
We have solved the time-fractional heat
conduction equation with the Caputo fractional derivative in the case of one
spatial variable in spherical coordinates. The heat absorption is assumed to be
proportional to temperature. The fundamental
solutions to the Cauchy problem and to the source problem have been studied. It
should be noted that in the case of the classical parabolic heat conduction
equation (![]() ), the
fundamental solutions to the Cauchy problem and to the source problem coincide,
whereas for
), the
fundamental solutions to the Cauchy problem and to the source problem coincide,
whereas for ![]() they are different.
The results of numerical calculations are displayed in figures for different
values of the parameter
they are different.
The results of numerical calculations are displayed in figures for different
values of the parameter ![]() describing heat absorption and the order of
the Caputo fractional derivative. The particular cases of the solutions corresponding to the value
describing heat absorption and the order of
the Caputo fractional derivative. The particular cases of the solutions corresponding to the value ![]() coincide with those
obtained in [4, 25]. The influence of the sign change of the parameter
coincide with those
obtained in [4, 25]. The influence of the sign change of the parameter ![]() on temperature is easily observable
from the figures. To calculate the Mittag-Leffler functions
on temperature is easily observable
from the figures. To calculate the Mittag-Leffler functions ![]() in (20) and
in (20) and ![]() in
(33), we have used the algorithms suggested in [29]. It should be emphasized
that fractional heat conduction and fractional diffusion have the same origin.
At the level of individual particle
motions the classical diffusion corresponds to Brownian motion with a
mean-squared displacement increasing linearly with time. Anomalous diffusion,
which is exemplified by a mean-squared displacement with the power-law
time dependence and was observed in different media [13, 30-32], is described
by equations with fractional derivatives.
in
(33), we have used the algorithms suggested in [29]. It should be emphasized
that fractional heat conduction and fractional diffusion have the same origin.
At the level of individual particle
motions the classical diffusion corresponds to Brownian motion with a
mean-squared displacement increasing linearly with time. Anomalous diffusion,
which is exemplified by a mean-squared displacement with the power-law
time dependence and was observed in different media [13, 30-32], is described
by equations with fractional derivatives.
References
[1] Povstenko Y., Fractional heat conduction equation and associated thermal stresses, J. Thermal Stresses 2005, 28, 83-102.
[2] Povstenko Y., Thermoelasticity which uses fractional heat conduction equation, J. Math. Sci. 2009, 162, 296-305.
[3] Povstenko Y., Non-axisymmetric solutions to time-fractional diffusion-wave equation in an infinite cylinder, Fract. Calc. Appl. Anal. 2011, 14, 418-435.
[4] Povstenko Y., Linear Fractional Diffusion-Wave Equation for Scientists and Engineers, Birkhäuser, New York 2015.
[5] Gorenflo R., Mainardi F., Fractional calculus: integral and differential equations of fractional order, [In:] A. Carpinteri, F. Mainardi (eds.), Fractals and Fractional Calculus in Continuum Mechanics, Springer, Wien 1997, 223-276.
[6] Podlubny I., Fractional Differential Equations, Academic Press, San Diego 1999.
[7] Kilbas A., Srivastava H., Trujillo J., Theory and Applications of Fractional Differential Equations, Elsevier, Amsterdam 2006.
[8] Hilfer R. (ed.), Applications of Fractional Calculus in Physics, World Scientific, Singapore 2000.
[9] West B.J., Bologna M., Grigolini P., Physics of Fractals Operators, Springer, New York 2003.
[10] Magin R.L., Fractional Calculus in Bioengineering, Begell House Publishers, Connecticut 2006.
[11] Mainardi F., Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models, Imperial College Press, London 2010.
[12] Leszczyński J.S., An Introduction to Fractional Mechanics, The Publishing Office of Częstochowa University of Technology, Częstochowa 2011.
[13] Uchaikin V.V., Fractional Derivatives for Physicists and Engineers, Springer, Berlin 2013.
[14] Atanacković T.M., Pilipović S., Stanković B., Zorica D., Fractional Calculus with Applications in Mechanics, John Wiley & Sons, Hoboken 2014.
[15] Povstenko Y., Fractional Thermoelasticity, Springer, New York 2015.
[16] Crank J., The Mathematics of Diffusion, 2nd ed., Oxford University Press, Oxford 1975.
[17] Carslaw H.S., Jaeger J.C., Conduction of Heat in Solids, 2nd ed., Oxford University Press, Oxford 1959.
[18] Polyanin A.D., Handbook of Linear Partial Differential Equations for Engineers and Scientists, Chapman & Hall/CRC, Boca Raton 2002.
[19] Nyborg W.L., Solutions of the bio-heat transfer equation, Phys. Med. Biol. 1988, 33, 785-792.
[20] Abad E., Yuste S.B., Lindenberg K., Survival probability of an immobile target in a sea of evanescent diffusive or subdiffusive traps: a fractional equation approach, Phys. Rev. E 2012, 86, 061120.
[21] Sokolov I.M., Schmidt M.G.W., Sagués F., Reaction-subdiffusion equations, Phys. Rev. E 2006, 73, 031102.
[22] Henry B.I., Langlands T.A.M., Wearne S.L., Anomalous diffusion with linear reaction dynamics: from continuous time random walks to fractional reaction-diffusion equations, Phys. Rev. E 2006, 74, 031116.
[23] Abad E., Yuste S.B., Lindenberg K., Reaction-subdiffusion and reaction-superdiffusion equations for evanescent perticles performing continuous-time random walks, Phys. Rev. E 2010, 81, 031115.
[24] Méndez V., Fedotov S., Horsthemke W., Reaction-Transport Systems: Mesoscopic Foundations, Fronts, and Spatial Instabilities, Springer, Berlin 2010.
[25] Povstenko Y., Fundamental solutions to central symmetric problems for fractional heat conduction equation and associated thermal stresses, J. Thermal Stresses 2008, 31, 127-148.
[26] Sneddon I.N., The Use of Integral Transforms, McGraw-Hill, New York 1972.
[27] Tikhonov A.N., Samarskii A.A., Equations of Mathematical Physics, Dover, New York 1990.
[28] Prudnikov A.P., Brychkov Yu.A., Marichev O.I., Integrals and Series. Vol. 1: Elementary Functions, Gordon and Breach, Amsterdam 1986.
[29] Gorenflo R., Loutchko J., Luchko Yu., Computation of the Mittag-Leffler function and its derivatives, Fract. Calc. Appl. Anal. 2002, 5, 491-518.
[30] Ben-Avraham D., Havlin S., Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, Cambridge 2000.
[31] Metzler R., Klafter J., The random walk’s guide to anomalous diffusion: a fractional dynamics approach, Phys. Rep. 2000, 339, 1-77.
[32] Metzler R., Klafter J., The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics, J. Phys. A: Math. Gen. 2004, 37, R161-R208.

