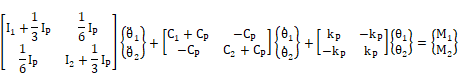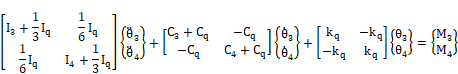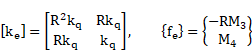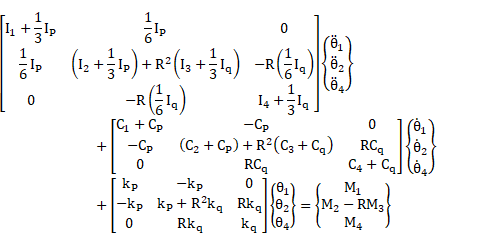The effect of damping coefficients on the torsional vibration of the damped multi-branch gears system
Jabbar Firouzi
,Hassan Ghassemi
,Karim Akbari Vakilabadi
,Hadi Khalilnezhad
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE EFFECT OF DAMPING COEFFICIENTS ON THE TORSIONAL VIBRATION OF THE DAMPED MULTI-BRANCH GEARS SYSTEM
Jabbar Firouzi 1, Hassan Ghassemi 1, Karim Akbari Vakilabadi 2, Hadi Khalilnezhad 2
1
Department of Maritime Engineering, Amirkabir University of Technology
Tehran, Iran
2 Department of Mechanic Engineering, Imam Khomeini University of
Marine Science
& Technology,
Nowshahr, Iran
gasemi@aut.ac.ir
Received: 22 October 2017;
Accepted: 29 December 2017
Abstract. The effect of the damping coefficients has been considered to estimate the torsional vibration of the multi-branch gears systems. In this paper, the effect of the viscous damping between the gears and the fluid in which the gear is working and the effect of the structural damping of the shafts in a three-branched gear system is investigated. Initially, the governing equations were derived and then the damping effects were studied using MATLAB code. In order to validate the results which prepared by MATLAB code are compared with the other computational methods. To investigate the effects of the stiffness and damping on the shafts and gears, different gear branch systems are considered. Some of the vibration results on the damped gear branched systems with viscous damper and structural damper are analyzed and discussed.
MSC 2010: 30, 34D99, 74H45
Keywords: torsional vibration, gear branch system, damped system, undamped system
1. Introduction
In analysing the vibrations of continuous structures, identification and modelling of damping are of particular importance and complexity. This complexity has led to the analysis of structures either without damping or simple damping with approximations of real state [1]. A torsional vibration is a phenomenon that can cause the axial cutting to be in the centre of the rotary shaft due to the twisting of the centre, so this should be considered when designing the shaft. In marine vessels, the vibration in the shaft connecting the engine to the propeller is due to the inharmonious excitation resulting from these two parts. So, the study of the torsional vibration of the transmission shaft is vital for moving the ship. In the systems with torsional vibration, linear values with angular values are replaced in vibrational equations.
Many engineering vibration problems can be solved with the theory of a degree of freedom (DOF) system. Complex systems may have several DOF. The standard method for solving such systems, if the DOF is not more than three degrees, is to obtain the equations of motion by Newton’s law of motion, the influence coefficient method, or by the Lagrange equations. Then differential equations of motion are solved by assuming an appropriate solution. If the DOF increases, solving differential equations of motion becomes more complicated for damped system [2]. Lin et al. showed that vibration propagation in complex ship structures at low frequencies can be attenuated by imposing irregularities to the ring frame locations in ships [3].
The natural frequency analysis for gear shaft systems is of practical importance and has a high sensitivity to the optimal design of these systems [4]. The torsional vibration in the marine power transmission system is usually very dangerous for the shaft line and the crankshaft [5]. So damping always exists in marine propulsion systems. Torsional damping may come from several sources, for example, shaft material, bearings, couplings, torsional vibration dampers, aerodynamic damper, etc. Shaft material or hysteretic dampers are due to the interaction of shaft material molecules, which leads to an increase in the material temperature of the shaft. A torsional vibration damper is a part that can be used in the connections between two-shaft cross-sections. The gear aerodynamic damping occurs due to interaction of the gear with the working fluid (such as steam, gas, air, etc.), lubricant, and coolant; which results in dissipation of the energy in the form of heat.
In other studies, the finite element method (FEM) has been used to solve the torsional vibration problems of direct and gear-branch systems [6]. Wu et al. have modelled the gearbox systems by elimination the twisting angles of the gears engaged decrease them to the direct equivalent system (or direct transmitted). Then, the overall mass matrix, damping matrix, stiffness matrix, and the torque vector were obtained from the direct transmitted system by the conventional FEM, and then obtained the natural frequencies and the mode shapes of the system [7]. For torsional vibration investigating of the crankshaft, it is assumed by 2-DOF and its stiffness is infinite. Also, due to insignificant influence, damping coefficients on the natural frequencies and the mode shapes of the devices were ignored from the damping coefficients matrix in solving the governing equations [8].
Drew et al. described two new test methods that were investigated for their suitability as methods of determining the torsional damping levels of the test gearbox of the back-to-back rig. The first test method investigated was to attempt a standard multi-input multi-output (MIMO) modal analysis of the gearbox test, in which the gearbox was used as a system with two inputs (torque per shaft) and the two output (angular velocity per shaft) was considered. The second test method was to assume the shape of a model for the test gearbox to match the calculation of the reacceptances for the gearbox and adjust the damping level in the model until it matched the experimental results [9].
Equipment failures due to torsional vibration are an important problem in the industry. Low torsional damping levels cause high stresses. Gearboxes are an important part of the marine power transmission system, so measuring the natural frequency of torsional vibration and investigate the effects of damping are of particular importance [10].
The effects of the stiffness and damping on both shafts and gears are important in multi-branch systems. Zou et al. employed a modal synthesis method for analysis the torsional vibration of the system. In this method, the system is divided into several subsystems and then solved by FEM [11]. Also, Ray presented a FEM of torsional vibration in geared shafts [12].
In research carried out by Murawski and Charchalis, the torsional vibration of the power transmission system was investigated by modelling the propeller, propeller shaft, middle shaft and main engine. In their research, numerical analysis was performed based on the FEM with experimental data measured by an experienced team, which was highly accurate and had an error rate of less than 6% [8].
Study of the ship propeller shaft vibrations is of particular importance. In this regard, the added mass and damping matrices of the propeller have an influence on the vibrational characteristics of the propulsion system. Mao and Young [13] have investigated the influence of the skew angle on the added mass and damping matrices, whose obtained results show that the increase in the Skew angle effects of the sway, heave, pitch and yaw components of the added mass and damping matrices, while the influence on the surge and roll components is negligible [13].
Aureli et al. modelled a rectangular thin cross section cantilever beam using the Euler-Bernoulli beam theory and investigated bending vibration in a high-viscosity fluid. The results of this study show that increasing the frequency and amplitude of the vibration causes vortex shedding and convection phenomena [14]. Firouzi and Ghassemi have recently presented the effect of variations in shaft diameter and torsional stiffness on the whirling speed of the ship propeller shafting system for systems that directly or indirectly attached the propeller to the engine [15]. Piatkowski used the algorithm phase-amplitude interpolation to create contours charts and estimate the shaft torsional vibrations and transient operating conditions of rotary machines [16].
The following sections are organized as follows. Governing equations are described in Section 2. Validation is given in Section 3. Vibration analysis of the damped gear branched system are presented in Section 4, and Section 5 is given for the conclusions.
2. Governing equations
Power transmission systems have many elements
such as shaft, gearbox, coupling, bearings and stern tube between the engine to
the propeller. Their tasks are to deliver the power from the engine to the
propeller to provide forward speed to the ship. Here, we consider a gear
branched system as shown in Figure 1. It has two shafts and 4 gears with
stiffness and damping. All of the consideration parameters define the mass
momentum of inertia of the shafts ![]() and
and ![]() , the mass momentum of
inertia of the gears
, the mass momentum of
inertia of the gears ![]() (
(![]() = 1 – 4), the damping of each gear
= 1 – 4), the damping of each gear ![]() (
(![]() = 1 – 4), torsional dampers of
different segments of the shaft
= 1 – 4), torsional dampers of
different segments of the shaft ![]() and
and ![]() , and torsional
stiffness of shafts
, and torsional
stiffness of shafts ![]() and
and ![]() .
.
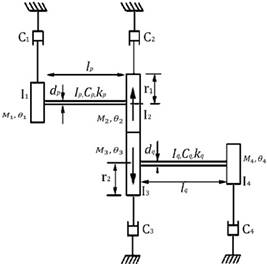
Fig. 1. Gear branched system
We write the vibrational equations of the above system as follows:
|
|
|
||||
|
|
|
||||
|
|
|
||||
|
|
|
Then for each shaft we write the above equations in matrix form.
|
|
||||
|
|
where: ![]() and
and ![]() the mass moment of
inertia and torsional stiffness of the shaft
the mass moment of
inertia and torsional stiffness of the shaft ![]() , respectively, also for shafts
, respectively, also for shafts ![]() the mass moment of the
inertia and torsional stiffness of the shaft are obtained.
the mass moment of the
inertia and torsional stiffness of the shaft are obtained.
Using the ratio between gears 2 and 3:
|
|
|
The negative sign R is due to the
opposite direction ![]() to
to![]() . Since
. Since ![]() and
and ![]() are the radius of the
gears 2 and 3, respectively. R is the gear ratio. Relations between the
shafts
are the radius of the
gears 2 and 3, respectively. R is the gear ratio. Relations between the
shafts ![]() and
and ![]() with considering the gear ratio, the following equations are
defined:
with considering the gear ratio, the following equations are
defined:
|
|
|
By derivation of equation (8) we have:
| (9) |
where:
| (10) |
In the above equations, ![]() represents the vector
of the column and
represents the vector
of the column and ![]() represents the
transformation matrix to remove the dependence of the angular displacement
represents the
transformation matrix to remove the dependence of the angular displacement![]() . By replacing the
equations (8), (9) in equation (6) and multiplying the two sides of the
resulting equation in
. By replacing the
equations (8), (9) in equation (6) and multiplying the two sides of the
resulting equation in ![]() we will have:
we will have:
| (11) |
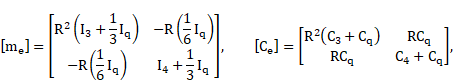 |
|
|
Thus, the mass matrix ![]() , the damping matrix
, the damping matrix ![]() , the hard matrix
, the hard matrix ![]() and the load vector
and the load vector ![]() of the drive shaft q
are defined by equations (12). If
of the drive shaft q
are defined by equations (12). If ![]() = –1,
similar relations are obtained for the drive shaft
= –1,
similar relations are obtained for the drive shaft ![]() (according to equation (1)).
In other words, the equation (12) is the key word of the method.
(according to equation (1)).
In other words, the equation (12) is the key word of the method.
|
|
3. Validation
In this work, the governing equations of the torsional vibration of the multi-branch gears system are derived and free vibration is considered. Overall mass, damping and torsional stiffness matrices were obtained, and a MATLAB code was used for solving and obtaining natural frequencies of the system. To verify the results, the system shown in Figure 2 was considered. Our results were compared with the results shown in Table 2, and they were in good conformity.
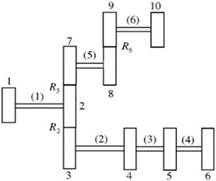
Fig. 2. The original three-branched gear system
For the original three-branched gear system, shown in Figure 2, the main dimensions and physical properties of the gears and shafts are presented in Table 1.
In fact, the given data, the mass moment of
inertia for the gears,![]() (
(![]() = 1 – 10) and the torsional stiffness of the
shafts
= 1 – 10) and the torsional stiffness of the
shafts ![]() (
(![]() = 1 – 6) are shown in Table 1. Also,
other data such as the diameter of the gears
= 1 – 6) are shown in Table 1. Also,
other data such as the diameter of the gears![]() , the diameter of the
shaft
, the diameter of the
shaft![]() , and the
length of the shaft
, and the
length of the shaft ![]() are given in this
table. For gears and shafts
are given in this
table. For gears and shafts ![]() = 20.2063 kg/m3
and
= 20.2063 kg/m3
and ![]() = 79.29·109 N/m2,
= 79.29·109 N/m2,
![]() =
= ![]() = 2.318,
= 2.318,
![]() =
= ![]() = 4.8182 and
= 4.8182 and
![]() =
= ![]() = 8.4906
is gear ratio.
= 8.4906
is gear ratio.
Table 1
Main dimensions and physical properties of shafts and gears
|
Gear |
Shaft |
|||||
|
No.
|
Mass moments
of inertia
|
Diameters |
No.
|
Torsional stiffness |
Diameters
|
Lengths
|
|
1 |
1098.213 |
1.69 |
1 |
0.6169 |
0.127 |
3.283 |
|
2 |
111.448 |
1.3 |
2 |
0.1966 |
0.102 |
4.219 |
|
3 |
4.067 |
0.56 |
3 |
3.9861 |
0.102 |
0.208 |
|
4 |
45.985 |
1.039 |
4 |
7.7621 |
0.102 |
0.107 |
|
5 |
26.438 |
0.908 |
5 |
0.2192 |
0.102 |
3.784 |
|
6 |
26.438 |
0.908 |
6 |
0.2429 |
0.064 |
0.521 |
|
7 |
0.407 |
0.27 |
|
|
|
|
|
8 |
33.895 |
1.2192 |
|
|
|
|
|
9 |
0.0407 |
1.431 |
|
|
|
|
|
10 |
9.2196 |
0.698 |
|
|
|
|
The natural
frequencies of the torsional vibration of the above system are presented in the
following table in two states with/without of the shafts mass.
The first frequency obtained is zero (![]() = 0) and other natural frequencies are given and compared in
Table 2.
= 0) and other natural frequencies are given and compared in
Table 2.
Table 2
Several of the lowest natural frequencies of the original three-branched gear system
|
|
|
|
|
|
|
Shaft mass |
|
Present method |
23.087 |
41.2902 |
215.2224 |
376.6524 |
710.4798 |
considered |
|
23.089 |
41.3231 |
217.6014 |
376.9155 |
712.6998 |
neglected |
|
|
FEM [2] |
23.087 |
41.2902 |
215.2224 |
376.6524 |
710.4786 |
considered |
|
23.089 |
41.3228 |
217.6013 |
376.9155 |
712.6985 |
neglected |
|
|
FEM [10] |
23.089 |
41.3228 |
217.6013 |
376.9155 |
712.6985 |
neglected |
|
Holzer [9] |
23.092 |
41.3290 |
217.9722 |
376.9155 |
713.3585 |
neglected |
4. Vibration analysis of the damped gear branched system
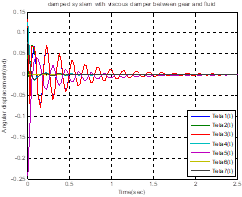
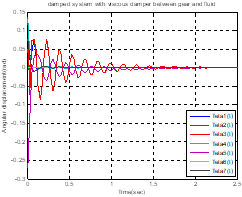
This example is given for vibration analysis of the damped gear branched system. It includes stiffness on the shaft and damping on both shafts and gears in two states as shown in Figure 3.
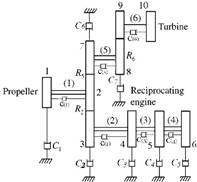
Fig. 3. The three-branched gear system with viscous damper and with structural damper
4.1. Vibration analysis of a damped gear branched system with viscous damper
We consider the analysis of the damped gear
branched system with the damper between the gears and fluid, as shown in Figure
3. In this case, the structural damper is equal to zero ![]() (
(![]() = 1 – 6) = 0.
= 1 – 6) = 0.
The damping coefficients for the seven
dampers shown in the figure above,
![]() (
(![]() = 1 – 7), were assumed to be the same. We study the influence of damping with consideration of the mass of all shafts
for different cases
= 1 – 7), were assumed to be the same. We study the influence of damping with consideration of the mass of all shafts
for different cases ![]() = 9 – 11.7 N m s/rad
and
= 9 – 11.7 N m s/rad
and ![]() (
(![]() = 2 – 7) = 100 – 130 N m s/rad.
The real part (
= 2 – 7) = 100 – 130 N m s/rad.
The real part (![]() ) of the special values of (
) of the special values of (![]() ·
·![]() = 1 – 6) is related to the damping parameter and the imaginary part (
= 1 – 6) is related to the damping parameter and the imaginary part (![]() ) to the damping
natural frequencies, whose values are shown in Table 3.
) to the damping
natural frequencies, whose values are shown in Table 3.
Table 3
Influence of damping on the natural frequencies of the damped gear branched system with the viscous damper
|
Damping coefficient
|
Eigenvalues |
||||||
|
|
|
|
|
|
|
Remarks |
|
|
|
0.01 23.08 |
1.52 41.29 |
9.87 217.36 |
1.49 376.91 |
1.30 712.69 |
1.87 828.36 |
|
|
1.1 |
0.02 23.08 |
1.68 41.28 |
10.86 217.31 |
1.64 376.91 |
1.43 712.69 |
2.06 828.36 |
|
|
1.2 |
0.02 23.08 |
1.83 41.28 |
11.85 217.26 |
1.79 376.91 |
1.56 712.69 |
2.25 828.36 |
|
|
1.3 |
0.02 23.08 |
1.98 41.27 |
12.84 217.20 |
1.93 376.91 |
1.69 712.69 |
2.43 828.36 |
|
As shown in Table 3, we increase the value of
![]() in the three steps by
adding 10% at each step. By increasing the value of
in the three steps by
adding 10% at each step. By increasing the value of![]() , the natural frequency
values of the damping (
, the natural frequency
values of the damping (![]() ) slightly increase
while (
) slightly increase
while (![]() ) does not almost
change.
) does not almost
change.
|
|
|
||
|
|
|
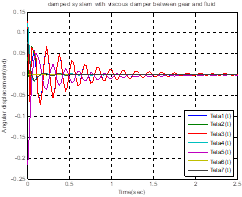
Fig. 4. Damped system with viscous
damper between gears and fluid (a) for ![]() (b) for 1.1
(b) for 1.1 ![]() (c) for 1.2
(c) for 1.2 ![]() (d) for 1.3
(d) for 1.3 ![]()
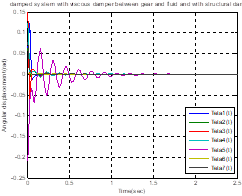
In Figure 4, by increasing the amount of
damping coefficient ![]() , the torsional
vibration amplitude increases at initial times and the torsional vibration in
, the torsional
vibration amplitude increases at initial times and the torsional vibration in ![]() and
and ![]() will be damped later
than the other parts. By increasing the amount of damping coefficient
will be damped later
than the other parts. By increasing the amount of damping coefficient![]() , the duration of the
damping is also reduced.
, the duration of the
damping is also reduced.
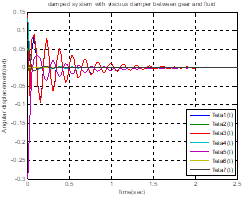
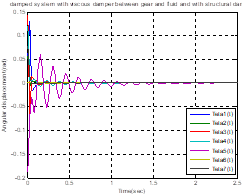
4.2. Vibration analysis of a damped gear branched system with viscous damper and structural damper
We consider Figure 3 for analysis of the
damped gear branched system with
the viscous damper and structural damper. In this case, consider the values of ![]() as before and consider the structural damping coefficients for shafts equal to
as before and consider the structural damping coefficients for shafts equal to ![]() , (
, (![]() = 1 – 6) = 150 – 195 N m s/rad.
The values obtained for the damping natural frequency (
= 1 – 6) = 150 – 195 N m s/rad.
The values obtained for the damping natural frequency (![]() ) and the damping
parameter (
) and the damping
parameter (![]() ) are given in Table 4.
) are given in Table 4.
Table 4
Influence of damping on the natural frequencies of the damped gear branched system with viscous damper and with structural damper
|
Damping coefficient
|
Eigenvalues |
||||||
|
|
|
|
|
|
|
Remarks |
|
|
|
0.09 23.08 |
2.16 41.26 |
25.62 216.10 |
4.97 376.83 |
161.48 694.16 |
9.84 828.30 |
|
|
1.1 |
0.10 23.08 |
2.36 41.25 |
27.85 215.83 |
5.40 376.9182 |
174.17 691.08 |
10.65 828.29 |
|
|
1.2 |
0.11 23.08 |
2.58 41.23 |
30.38 215.49 |
5.88 376.80 |
190.00 686.90 |
11.26 828.27 |
|
|
1.3 |
0.12 23.08 |
2.79 41.22 |
32.92 215.12 |
6.37 376.78 |
205.84 682.32 |
12.58 828.26 |
|
|
|
|
||
|
|
|
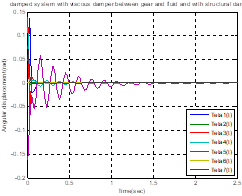
Fig. 5. Damped
system with viscous damper and with structural damper (a) for ![]() ,
(b) for 1.1
,
(b) for 1.1 ![]() , 1.1
, 1.1 ![]() (c) for 1.2
(c) for 1.2 ![]() , 1.2
, 1.2 ![]() (d) for 1.3
(d) for 1.3 ![]()
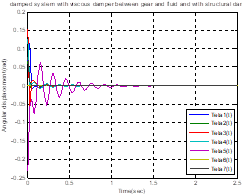
In Table 4, we increase the amount of ![]() and
and ![]() in the three steps at
each step by the amount of 10%. By increasing these values, the damping natural
frequency (
in the three steps at
each step by the amount of 10%. By increasing these values, the damping natural
frequency (![]() ), other than for
), other than for ![]() , is not significantly
reduced in the other cases, but in all cases the values of the damping
parameter (
, is not significantly
reduced in the other cases, but in all cases the values of the damping
parameter (![]() ) increase. In Figure
5, increasing the amount of damping coefficient
) increase. In Figure
5, increasing the amount of damping coefficient ![]() and
and ![]() , the torsional
vibration amplitude increases at initial times and torsional vibration at
, the torsional
vibration amplitude increases at initial times and torsional vibration at ![]() will be damped later
than other parts. As the number of damping coefficients increases, the duration
of the damping also decreases.
will be damped later
than other parts. As the number of damping coefficients increases, the duration
of the damping also decreases.
5. Conclusions
The effect of the damping coefficients has been achieved to estimate the torsional vibration of the multi-branch gears systems. Based on the presented computational results, the following conclusions are drawn:
1. Increased damping leads to an increase in the torsional vibration amplitude in the initial times, and this issue is very important in the vibration and should increase the damping coefficient, especially in different parts of the engine for any reason (oil reduction, erosion, etc.) is prevented.
2. With a structural damper applied to the shafts and the gears, the torsional vibration amplitude is lower than that for which only the viscous damper was considered.
3. Increased damping, in particular structural damping, leads to a reduction in the damping time of the vibration amplitude, but, on the other hand, causes energy dissipation.
It is our spirit to investigate on the stiffness of gearwheel teeth in near future. In this regard, all dynamics equations are required to be obtained. The MATLAB code should be improved and employed with new examples of the stiffness effect of the gearteeth.
References
[1] Wilson W.K., Practical Solution of Torsional Vibration Problems, 3rd edition, Vol 1&2, Chapman & Hall, London 1956 and 1963.
[2] Mohta Brijgopal R., Evaluation of methods for analysis of multi-degree-of-freedom systems with damping, Masters Theses, 5272, 1968.
[3] Lin T.R., Pan J., O’Shea P.J., Mechefske Ch.K., A study of vibration and vibration control of ship structures, Marine Structures 2009, 22, 730-743.
[4] Liu Z.S., Chen S.H., Derivatives of eigenvalues for torsional vibration of geared shaft systems, Journal of Vibration and Acoustics 1993, 115, 277-279.
[5] Brydum L., Jakobsen S.B., Vibration characteristics of two-stroke, low speed diesel engines, MAN B&W Diesel, Copenhagen 1987, 1-16.
[6] Kushwaha V., Analysis of torsional vibration characteristics for multi-rotor and gear-branched systems using FEM, National Institute of Technology, Rourkela 2012, 4, 39-41.
[7] Wu J.S., Chen C.H., Torsional vibration analysis of gear-branched systems by finite element method, Journal of Sound and Vibration 2001, 240(1), 159-182.
[8] Murawski L., Charchalis A., Review simplified method of torsional vibration calculation of marine power transmission system, Marine Structures 2014, 39, 335-349.
[9] Drew S.J., Stone B.J., Torsional damping measurements for a gearbox, Mechanical Systems and Signal Processing 2005, 19, 1096-1106.
[10] Drew S.J., Stone B.J., Torsional damping of a back-to-back gearbox rig, Proc. Instn. Mech. Engrs. 2002, 216 Part K, 157-168.
[11] Zou CH.P., Chen D.Sh., Hua H.X., Torsional vibration analysis of complicated multi-branched shafting systems by MSM, Journal of Vibration and Acoustics 2003, 125, 317-323.
[12] Ray D., A Study on FEA of Torsional Vibration in Geared Shafts, National Institute of Technology, Rourkela 2010, 2, 25-27.
[13] Mao Y., Young Y.L., Influence of skew on the added mass and damping characteristics of marine propellers, Ocean Engineering 2016, 121, 437-452.
[14] Aureli M., Basaran M.E., Porfiri M., Nonlinear finite amplitude vibrations of sharp-edged beams in viscous fluids, Journal of Sound and Vibration 2012, 331, 1624-1654.
[15] Firouzi J., Ghassemi H., The effect of the shaft diameter and torsional stiffness on the whirling speed of the ship propeller shafting system, Journal of Mechanical Design and Vibration 2017, 5, 37-42.
[16] Piatkowski J., The visualization of shaft vibration using the algorithm of phase-amplitude data interpolation, Journal of Applied Mathematics and Computational Mechanics 2016, 15(1), 137-148.