The stability conditions of the cubic damping Van der Pol-Duffing oscillator using the HPM with the frequency-expansion technology
Yusry O. El-Dib
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE STABILITY CONDITIONS OF THE CUBIC DAMPING VAN DER POL-DUFFING OSCILLATOR USING THE HPM WITH THE FREQUENCY-EXPANSION TECHNOLOGY
Yusry O. El-Dib
Department of Mathematics, Faculty of
Education
Ain Shams University, Roxy, Cairo, Egypt
yusryeldib52@hotmail.com
Received: 13 July 2018;
Accepted: 15 October 2018
Abstract. In this paper, we perform the frequency-expansion formula for the nonlinear cubic damping van der Pol’s equation, and the nonlinear frequency is derived. Stability conditions are performed, for the first time ever, by the nonlinear frequency technology and for the nonlinear oscillator. In terms of the van der Pol’s coefficients the stability conditions have been performed. Further, the stability conditions are performed in the case of the complex damping coefficients. Moreover, the study has been extended to include the influence of a forcing van der Pol’ oscillator. Stability conditions have been derived at each resonance case. Redoing the perturbation theory for the van der Pol oscillator illustrates more of a resonance formulation such as sub-harmonic resonance and super-harmonic resonance. More approximate nonlinear dispersion relations of quartic and quintic forms in the squaring of the extended frequency are derived, respectively.
MSC 2010: 34D, 35B10, 35B20, 35B35, 37C75, 41A58, 42A10
Keywords: homotopy perturbation method, nonlinear oscillators, cubic nonlinear damping van der Pol’s equation, nonlinear frequency analysis, stability analysis
1. Introduction
In the present paper, the stability criteria for the dynamics of a Van der Pol-Duffing oscillator are considered. This equation is one of the most interesting and important collective behaviors in non-linear dynamics. Many efforts have been made to approximate the solutions of this equation or to construct simple maps that qualitatively describe important features of the dynamics. The solutions of this equation are oscillations, which may have periodic forms or non-periodic, as well. We can mark off two cases: the unforced, which is autonomous (there is no excitation parameter) and the forced oscillator with excitation frequency, which is non-autonomous.
In recent years, several analytical methods such as homotopy perturbation [1], harmonic balance [2], residue harmonic balance [3], The Hamiltonian approach [4], homotopy analysis [5], max-min approach [6], coupling of homotopy variation [7], iterative homotopy harmonic balance method [8], global residue harmonic balance [9], Fourier series solutions with finite harmonic terms [10], amplitude-frequency formulation [11-13], parameter-expansion method [14-19], multi-step homotopy analysis method [20], multiple-scales homotopy perturbation method [21-23] and the Frobenius-homotopy method [24] have been developed for solving strongly nonlinear oscillators.
The system considered herein is an extended version of the well-known of the typical van der Pol’ oscillator, which is a paradigmatic model for the description of self-excited oscillations. Adding a cubic nonlinearity to the primary system, it is possible to obtain a large variation frequency [25]. This modified system is usually referred to as van der Pol-Duffing oscillator [26]. The Van der Pol-Duffing forced oscillator with the variation of the forced frequency are obtained and studied, based on the homotopy analysis method, by Jifeng Cui et al. [27]. In this work, the stability of the periodic solutions is obtained by use of Floquet theory.
The main idea of this work is to obtain the stability criterion for the generalized van der Pol-Duffing oscillator and to find approximate periodic solutions. In Ref. [18-20] the author has established the periodic solution and studied the stability behavior via the multiple-scales homotopy technique. Stability criteria have been established from the linear perturbation of the amplitude equation around the steady-state solution. In the present work, a new method is adopted to construct the stability criterion. The criterion has been established, for the first-time, via the homotopy frequency analysis. The derived of the nonlinear frequency proposed by scientists and engineers [14-18, 26] is the most effective and convenient method for handling nonlinear problems. In this method, the solution and unknown frequency of oscillation are expanding in a series by a bookkeeping parameter. The use of the nonlinear frequency in studying the stability behavior is a new tool that is important and powerful for solving nonlinear oscillator systems arising in nonlinear science and engineering.
2. Frequency analysis via homotopy perturbation method for the autonomous case
We consider the following equation, which is a generalization of cubic van der Pol’s-Duffing equation:
| (1) |
where ![]() , and
, and ![]() is the independent variable with the
initial conditions
is the independent variable with the
initial conditions ![]() The constants
The constants ![]() and
and ![]() are real. The remaining coefficients
are real. The remaining coefficients ![]() are, in general, complex constants. In order to solve this equation
via the homotopy perturbation technique, we define the two parts
are, in general, complex constants. In order to solve this equation
via the homotopy perturbation technique, we define the two parts
| (2) |
| (3) |
Construct the homotopy equation in the form
| (4) |
Considering the frequency analysis so that we define the following frequency expansion:
| (5) |
Assuming that the function ![]() has been expanded as
has been expanded as
| (6) |
Employing (5) and (6) with (4), equating the
identical powers of ![]() to zero, yields
to zero, yields
| (7) |
| (8) |
The solution of the zero-order problem leads to
| (9) |
Substituting (9) into (8), the requirement of no
secular term in ![]() needs
needs
| (10) |
| (11) |
The solution of (8) without secular terms yields
| (12) |
where ![]() has been replaced by
(11). If the first order approximation is enough, then setting
has been replaced by
(11). If the first order approximation is enough, then setting ![]() into expansion (6) the approximate
periodic solution can be readily obtained:
into expansion (6) the approximate
periodic solution can be readily obtained:
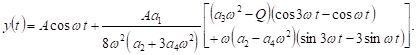 | (13) |
The approximate solution (13) is an oscillator
where the parameter ![]() has real
values. This requires formulating a dispersion relation including the argument
has real
values. This requires formulating a dispersion relation including the argument ![]() .
.
2.1. Stability conditions of cubic damping van der Pol’s nonlinear oscillator
In order to find the expression for the
nonlinear frequency ![]() , we substitute (10) into (5)
and setting
, we substitute (10) into (5)
and setting ![]() yields the approximate
nonlinear frequency, in terms of the amplitude
yields the approximate
nonlinear frequency, in terms of the amplitude ![]() ,
in the form
,
in the form
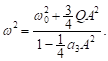 | (14) |
Removing the amplitude ![]() from (14) using (11) leads to
from (14) using (11) leads to
| (15) |
The necessary and sufficient condition for
stability is that ![]() must be a real
quantity. This constrains for stability can be achieved when the following
conditions on (15) are satisfied together:
must be a real
quantity. This constrains for stability can be achieved when the following
conditions on (15) are satisfied together:
| (16) |
These are the required conditions in order to obtain the oscillatory solution.
In order to
find the necessary and sufficient conditions for the existing the limit cycle,
we remove ![]() from
(11) using (14) yields
from
(11) using (14) yields
| (17) |
According to this approximate analysis, a limit
cycle will exist if the amplitude ![]() is
real. This requires the following relations:
is
real. This requires the following relations:
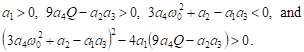 | (18) |
In fluid
mechanics, the damping coefficients ![]() and
and ![]() may appear in the complex
form. In order to obtain the stability criteria, in this case, one can
assume that
may appear in the complex
form. In order to obtain the stability criteria, in this case, one can
assume that ![]() be real in the characteristic equation
(15) separating the real and imaginary parts then employing the imaginary part
to the real part. The result represents a characteristic equation having real
coefficients. Therefore, for the
oscillatory solution, the requirement of
be real in the characteristic equation
(15) separating the real and imaginary parts then employing the imaginary part
to the real part. The result represents a characteristic equation having real
coefficients. Therefore, for the
oscillatory solution, the requirement of ![]() being
real yields the following stability conditions:
being
real yields the following stability conditions:
| (19) |
3. The non-autonomous case
We are now concerned with the excited, by a periodic external force, van der Pol-Duffing oscillator. This is the more general case, so we rewrite equation (1) with the forcing part included in
| (20) |
where ![]() and
and ![]() represent the amplitude and the frequency of the forcing part.
The application of the homotopy perturbation method allows several types
for
the primary part
represent the amplitude and the frequency of the forcing part.
The application of the homotopy perturbation method allows several types
for
the primary part ![]() . The chosen of
. The chosen of ![]() as defined by (2) will leads to study the
stability of the harmonic resonance case. Some changes in the homotopy
equation (4) is done whenever the
alternative choice for the primary part
as defined by (2) will leads to study the
stability of the harmonic resonance case. Some changes in the homotopy
equation (4) is done whenever the
alternative choice for the primary part ![]() of (20) is included the
forcing part. This case will lead to obtain the stability criteria at
sub-harmonic and super-harmonic resonance cases. These are the subject of the
next sections.
of (20) is included the
forcing part. This case will lead to obtain the stability criteria at
sub-harmonic and super-harmonic resonance cases. These are the subject of the
next sections.
3.1. Solution and stability conditions at the harmonic resonance case
We proceed as in the previous sections assuming that the homotopy equation has been built in the following form:
| (21) |
To discuss the exact resonance case, we assume
that the frequency of the periodic force ![]() is
equivalent to the nonlinear frequency
is
equivalent to the nonlinear frequency ![]() . The
requirements of obtaining the uniform solution at the resonance case lead to
the removal of the terms that producing secularity in the first-order problem
of (21), so we obtain
. The
requirements of obtaining the uniform solution at the resonance case lead to
the removal of the terms that producing secularity in the first-order problem
of (21), so we obtain
| (22) |
The function of ![]() without
secular terms has the form
without
secular terms has the form
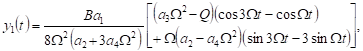 | (23) |
The first order approximate solution of the harmonic resonance case has the form
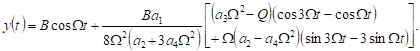 | (24) |
In this case, the frequency ![]() has satisfied the following dispersion
relation:
has satisfied the following dispersion
relation:
| (25) |
Since the forcing frequency ![]() is real, then the necessary and
sufficient stability conditions are
is real, then the necessary and
sufficient stability conditions are
| (26) |
These stability criteria occur for the system having real coefficients of the van der Pol-Duffing equation (21). Further, when these coefficients are in complex form, the stability conditions are present in the form
4. Further harmonic resonance cases for the non-autonomous problem
In the application of the homotopy
perturbation method, for the forcing
van der Pol’s damping nonlinear oscillator (20), there is an another chosen for
the primary part ![]() The
alternative is chosen [22] such that
The
alternative is chosen [22] such that
| (28) |
Redoing the homotopy perturbation method using the primary operator (28) leads to rearranging the homotopy equation (21) to become
| (29) |
Employing the two expansions (5) and (6),
assuming that ![]() , the primary
solution becomes
, the primary
solution becomes
| (30) |
We briefly now present the behavior of the equation (29) using a first-order approximation. Accordingly, the first-order perturbation is performed as
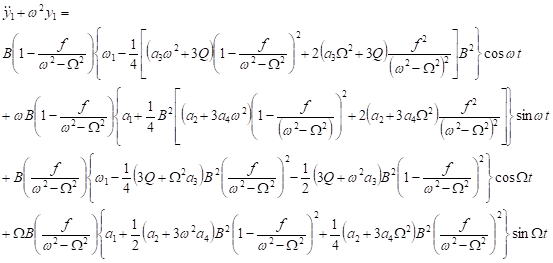 |
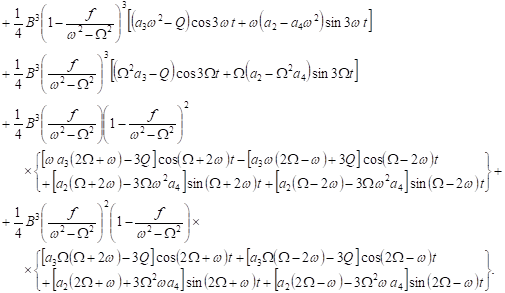 | (31) |
Three cases can be distinguished in analyzing
this case. The non-resonance
case, where the forcing frequency ![]() is away from the
nonlinear frequency
is away from the
nonlinear frequency ![]() ,
the sub-harmonic resonance case, which occurs as
,
the sub-harmonic resonance case, which occurs as ![]() and
the super-harmonic resonance case
which arises whence
and
the super-harmonic resonance case
which arises whence ![]()
4.1. The non-resonance case
In this case, the uniform solution for (31) is performed when the terms that producing secular terms absent. At this stage, we add the solution of (31) without secular terms to the primary solution (30) to produce the final first-order approximate solution in the form
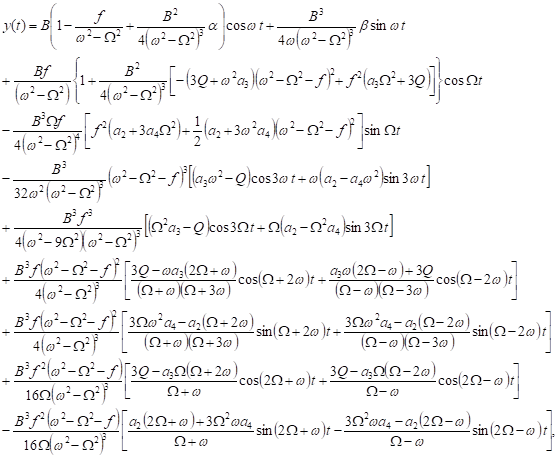 | (32) |
where the constants ![]() and
and ![]() are
are
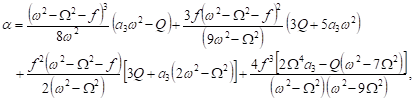 | (33) |
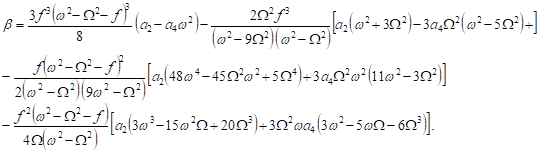 (34)
(34) |
As explained before, the result of removing the secular terms from equation (31) implied
| (35) |
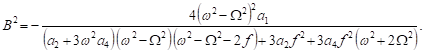 | (36) |
The above solvability conditions used to formulate the following nonlinear frequency that corresponds to the non-resonance case:
| (37) |
where the constants ![]() are:
are:
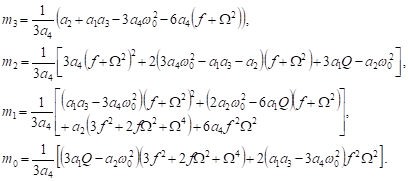 | (38) |
The requirement of all the eigenvalues for the characteristic equation (37) to be real needs all the four roots of (37) must be positive and real. From elementary algebra, the four roots are positive whence
| (39) |
There are three discriminants for the quartic polynomial to ensure the existences of the real roots [28]. The necessary and sufficient conditions, for all the eigen-values of (37) to be real, are
| (40) |
Conditions (39) and conditions (40) together represent the strict requirements to obtain the periodic solution.
4.2. The sub-harmonic resonance case
The sub-harmonic resonance case arises when
the frequency![]() has equivalent to
has equivalent to ![]() . In order to obtain periodic solutions
and to study the stability behavior at this resonance case, we need to remove
the additional secular terms that are found in equation (31). Removing of these
secularity leads to formulate the approximate nonlinear frequency, which
satisfied the following characteristic equation:
. In order to obtain periodic solutions
and to study the stability behavior at this resonance case, we need to remove
the additional secular terms that are found in equation (31). Removing of these
secularity leads to formulate the approximate nonlinear frequency, which
satisfied the following characteristic equation:
| (41) |
where ![]() are
real constants listed below:
are
real constants listed below:
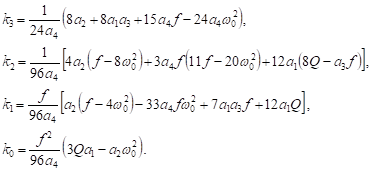 | (42) |
Accordingly, the uniform approximate first order solution has the final form:
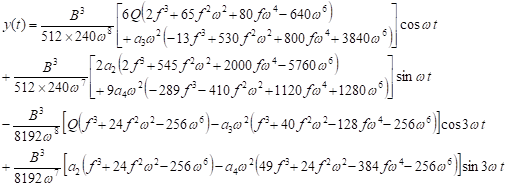 |
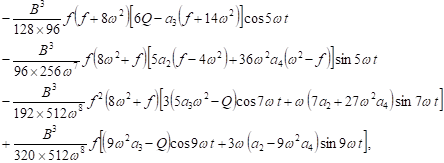 | (43) |
where the amplitude![]() in
this case has the form
in
this case has the form
| (44) |
As mentioned before, the stability conditions are derived in the form
| (45) |
4.3. The super-harmonic resonance case
When
the frequency W has
equivalent to ![]() , then we have the so-called the
super-harmonic resonance case. The first-order
approximate solution of the forcing van der Pol-Duffing equation (20), without
secular terms, is formulated in the
following form:
, then we have the so-called the
super-harmonic resonance case. The first-order
approximate solution of the forcing van der Pol-Duffing equation (20), without
secular terms, is formulated in the
following form:
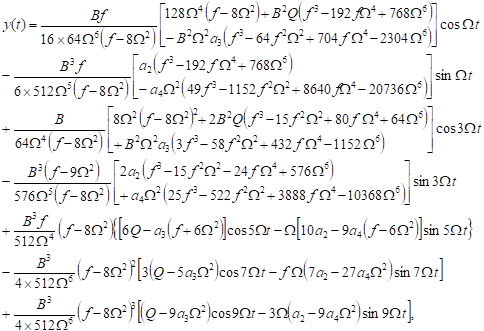 | (46) |
where the amplitude ![]() is given by
is given by
| (47) |
As a result of the removing the secular terms
from equation (31), taking into
account the case of ![]() , the characteristic equation has been evaluated in
the following form:
, the characteristic equation has been evaluated in
the following form:
| (48) |
The coefficients that appear in the above dispersion relation are:
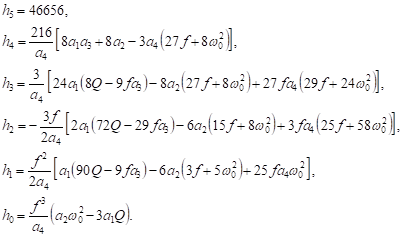 (49) (49) |
Stability conditions can be performed as follows:
Five changes of sign in the characteristic equation (48) signify the presence of positive roots. Therefore the requirements of positive roots are
| (50) |
The necessary and sufficient conditions for all roots of (48) to be real [28] are
| (51) |
Satisfying conditions (50) and conditions (51) together, ensure that the solution (46) has a periodic form.
5. Conclusions
In this work, we present the basic
theoretical efforts that are known in order
to deal with non-trivial solutions of the van der Pol oscillator. We obtain
analytic
approximation solutions for the generalized cubic van der Pol-Duffing equation.
We also construct a set of stability criteria in order to ensure the presence
of the
periodic solutions. The homotopy frequency method is used to derive an
expression for approximate nonlinear frequency for the autonomous case. The
derivation has been extended for the non-autonomous case where the forcing van
der Pol’s equation is considered. A polynomial with a quadratic form in the
nonlinear frequency ![]() is obtained for the
non-forcing van der Pol’s equation. In the presence of the forcing,
is obtained for the
non-forcing van der Pol’s equation. In the presence of the forcing, ![]() the nonlinear frequency has formulated as a quadratic form in
the nonlinear frequency has formulated as a quadratic form in ![]() at the harmonic resonance case. In the
case of the sub-harmonic resonance case, a polynomial of quartratic in
at the harmonic resonance case. In the
case of the sub-harmonic resonance case, a polynomial of quartratic in ![]() has been imposed. In
the final case, a quintic polynomial in
has been imposed. In
the final case, a quintic polynomial in ![]() has
been governed the super-harmonic res case. Periodic solutions are generated
under an urgent condition on the frequency
has
been governed the super-harmonic res case. Periodic solutions are generated
under an urgent condition on the frequency ![]() to
be a real quantity. This requires that all roots of the dispersion relations
must be real and positive quantities. Satisfying these requirements imposes
some conditions, for
the first-time, known as the stability conditions.
to
be a real quantity. This requires that all roots of the dispersion relations
must be real and positive quantities. Satisfying these requirements imposes
some conditions, for
the first-time, known as the stability conditions.
References
[1] He, J.H. (1999). Homotopy perturbation technique. Comput. Met. Appl. Mech. Eng., 178, 257-262.
[2] Mickens, R.E. (1996). Oscillations in Planar Dynamics Systems. Singapore: World Sci.
[3] Guo, Z., & Ma, X. (2014). Residue harmonic balance solution procedure to nonlinear delay differential systems. J. Appl. Math. Comp., 237, 20-30.
[4] Ju, P., & Xue, X. (2015). Global residue harmonic balance method for large-amplitude oscillations of a nonlinear system. J. Appl. Math. Model., 39, 449-454.
[5] He, J.H. (2010). Hamiltonian approach to nonlinear oscillators. Phys. Lett. A, 374, 2312-2314.
[6] Liao, S.J., & Cheung, A.T. (1998). Application of homotopy analysis method in nonlinear oscillations. ASME J. Appl. Mech., 65, 914-922.
[7] He, J.H. (2008). Max-min approach to nonlinear oscillators. Int. J. Nonlinear Sci. Numer. Simul., 9, 207-210.
[8] Akbarzede, M., Langari J., & Ganji D.D. (2011). A coupled homotopy variational method and variational formulation applied to nonlinear oscillators with and without discontinuities. ASME J. Vib. Acoust., 133, 044501.
[9] Guo, Z., & Leung, A.Y.T. (2010). The iterative homotopy harmonic balance method for conservative Helmholtz-Duffing oscillators. J. Appl. Math. Comp., 215, 3163-3169.
[10] Luo, A.C.J., & Yu, B. (2015). Complex period-1 motions in a periodically forced, quadratic nonlinear oscillator. J. Vib. Cont., 21(5), 896-906.
[11] He, J.H. (2006). Some asymptotic methods for strongly nonlinear equations. Internat. J. Modern Phys. B, 20, 1141-1199.
[12] He, J.H. (2008). An improved amplitude frequency formulation for nonlinear oscillators. Int. J. Nonlinear Sci. Numer. Simul., 9(2), 211-212.
[13] García, A.G. (2017). An amplitude-period formula for a second order nonlinear oscillator. Nonlinear Sci. Lett. A, 8(4), 340-347.
[14] Shou, H.D., & He, J.H. (2007). Application of parameter-expanding method to strongly nonlinear oscillators. Int. J. Nonlinear Sci. Numer. Simul., 8, 121-124.
[15] He, J.H. (2010). A note on the homotopy perturbation method. Thermal Science, 14(2), 565-568.
[16] He, J.H. (2014). Homotopy perturbation method with two expanding parameters. Indian Journal of Physics, 88(2), 193-196.
[17] He, J.H. (2012). Homotopy perturbation method with an auxiliary term. Abstract and Applied Analysis, DOI: 10.1155/2012/857612.
[18] El-Dib, Y.O. (2018). Stability of a strongly displacement time-delayed Duffing oscillator by the multiple-scales-homotopy perturbation method. J. of Appl. Compu. Mech., 4(4), 260-274.
[19] Wu, Y., & He, J.H. (2018). Homotopy perturbation method for nonlinear oscillators with coordinate dependent mass. Results in Physics, 10, 270-271.
[20] Ebenezer, B., Asamoah, J.K.K., Khan I., et al. (2017). The multi-step homotopy analysis method for a modified epidemiological model for measles disease. Nonlinear Sci. Lett. A, 8(3), 320-332.
[21] El-Dib, Y.O. (2017). Homotopy perturbation for excited nonlinear equations. Science and Engineering Applications, 2(1), 96-108.
[22] El-Dib, Y.O. (2017). Multiple scales homotopy perturbation method for nonlinear oscillators. Nonlinear Sci. Lett. A, 8(4), 352-364.
[23] El-Dib, Y.O. (2018). Periodic solution and stability behavior for nonlinear oscillator having a cubic nonlinearity time-delayed. Int. Ann. Sci., 5(1), 12-25.
[24] El-Dib, Y.O., & Moatimid, G.M. (2018). On the coupling of the homotopy perturbation and Frobenius method for exact solutions of singular nonlinear differential equations. Nonlinear Sci. Lett. A, 9(3), available online July 5, 220-230.
[25] Domany, E., & Gendelman, O.V. (2013). Dynamic responses and mitigation of limit cycle oscillations in Van der Pol-Duffing oscillator with nonlinear energy sink. J. Sound Vib., 332(21), 5489-5507.
[26] Guckenheimer, J., & Holmes, P. (1983). Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vectors Fields. New York: Springer-Verlag.
[27] Cui, J., Liang, J., & Lin, Z. (2016). Stability analysis for periodic solutions of the Van der Pol-Duffing forced oscillator. Physica Scripta, 91(1), 015201, 7p.
[28] Kurtz, D.C. (1992). A sufficient condition for all the roots of a polynomial to be real. The American Mathematical Monthly, 99(3), 259-263.

