The influence of inertia weight on the Particle Swarm Optimization algorithm
Dawid Cekus
,Dorian Skrobek
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
THE INFLUENCE OF INERTIA WEIGHT ON THE PARTICLE SWARM OPTIMIZATION ALGORITHM
Dawid Cekus, Dorian Skrobek
Institute of Mechanics and Machine Design
Fundamentals
Czestochowa University of Technology
Częstochowa, Poland
cekus@imipkm.pcz.pl, skrobek@imipkm.pcz.pl
Received: 10 September 2018;
Accepted: 30 January 2019
Abstract. The paper presents the use of the Particle Swarm Optimization (PSO) algorithm to find the shortest trajectory connecting two defined points while avoiding obstacles. The influence of the inertia weight and the number of population adopted in the first iteration of the PSO algorithm was examined for the length of the sought trajectory. Simulation results showed that the proposed method achieved significant improvement compared to the linearly decreasing method technique that is widely used in literature.
MSC 2010: 74P05, 65Y20, 65K10
Keywords: Particle Swarm Optimization, PSO algorithm, inertia weight, trajectory
1. Introduction
The most mobile robots or manipulators used in industry have a predefined optimum trajectory, but as a result of changes in a shop floor and production lines, there is a need to define a new work path. It often happens that the changes of workspaces are fluidly reorganized, meaning that the new trajectories’ work must be determined without delay. In this case, the trajectory can be searched again, but the newly found track may cause a change in the work cycle of several devices that work together. To avoid this inconvenience, a similar trajectory to the previous one must be found.
In this paper, we present the use of the Particle Swarm Optimization (PSO) algorithm [1, 2] to find the optimal 2D trajectory between two defined points. Moreover there are obstacles in the working space (Fig. 1).
2. Particle Swarm Optimization algorithm
The PSO algorithm is the result of observation of the phenomena occurring in nature, such as a school of fish or a horde of insects. Each particle swarm is able to remember and use their experience, which is taken from the process of iteration, and is also able to communicate with other members of the population.
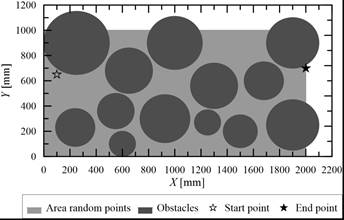
Fig. 1. Workspace
Particle Swarm Optimization was proposed in 1995 by Kennedy and Eberhart [1] and has been further modified by transformation of the equations of a motion of the particles (a combination of global and local versions) [3-6].
The PSO method is illustrated schematically in Figure 2.
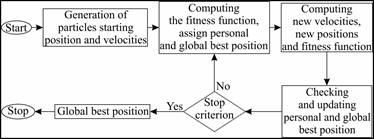
Fig. 2. Block diagram of the PSO algorithm [7, 8]
In the PSO algorithm, initial values (such as the position and velocity) of each particle in a swarm are random. Then, in the iteration step n+1, the velocities in the m direction are described as follows:
| (1) |
where χ is a constriction factor, w is the inertia weight determined at the level of the i-th particle, Vm(n) is a velocity in previous iteration step, c1 and c2 are cognitive and social parameters suitable, r1 and r2 are random numbers taken from [0,1], pm is a personal best position of the considered particle from the whole iteration process, gm is a global best position obtained by the entire swarm, Dt is a time step and xm(n) is a particle position in previous iteration step.
The new position for each particle in each test direction is equal to:
| (2) |
Before proceeding to the calculations, 15 auxiliary points, by which the sought trajectory runs, are drawn (Fig. 3).
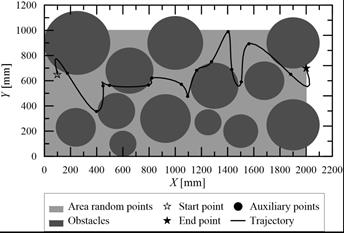
Fig. 3. The sought trajectory in the first iteration
The trajectory shown in Figure 3 is derived from the first iteration and is the result of interpolation by 17 points (15 auxiliary points, starting and end point). In the first iteration, this trajectory usually goes through obstacles or is outside the working area. The PSO algorithm is designed to find the shortest trajectory. To do this, the algorithm must “move” the points in such a way that the entire trajectory is in the solution search area and that the obstacles are avoided. If the trajectory goes through obstacles, the penalty function is taking account in the objective function [9].
In the PSO algorithm, a population size (pop = A + B + C) is equal 150. Each population contains 15 points randomly generated in the solution search area. The accepted population for the first iteration consists of the following parts:
·
the first element of the population joints the
starting point with the ending point (15 points are evenly distributed over the
entire length of the shortest trajectory) - this trajectory ignores obstacles: ![]() ,
,
·
n% of the remaining population (n
= 20, 60, 100) constitutes the points (15 points) drawn before the start of the PSO algorithm. They are identical for
each inertia weight: ![]() ,
,
·
the remaining part of the population consists of
randomly generated 15 points: ![]() .
.
In subsequent iterations, the position of the points from each population is changed in accordance with the operation of the PSO algorithm.
The following inertia weights have been analyzed during the test [10-13]:
| 1. | (3) |
| 2. | (4) |
| 3. | (5) |
| 4. | (6) |
| 5. | (7) |
6. 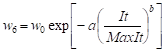 , , | (8) |
The variables in formulas (3)-(8) denote: MaxIt - maximum number of iterations (MaxIt = 300), It - current iteration, wdamp - damping factor (wdamp = 0.98), r - random numbers from the interval [0,1], a - local search attractor (a = 3), b - global search attractor (b = 1), w0 - initial inertia weight (w0 = 0.9), wmax - maximum value of the inertia weight (wmax = 1), wmin - minimum value of the inertia weight (wmin = 0.3).
Figure 4 shows all weights accepted for calculation. Each of the inertia weights (except for the fourth) is identical for each calculation attempt, since the fourth inertia weight is so-called noise in the range [0.5;1].
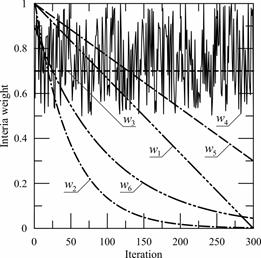
Fig. 4. Inertia weights
3. The sample numerical results
Each test for the adopted n% of population, for each inertia weight has been repeated ten times. It was assumed that the number of iterations is 300 and the population is 150. The results from the calculations are summarized in Tables 1-3.
Table 1. Length of trajectory for 20% of accepted population
|
|
w1 |
w2 |
w3 |
w4 |
w5 |
w6 |
|
L [mm] |
2041,38 |
1978,84 |
2142,56 |
2003,59 |
2541,56 |
2042,06 |
|
1978,34 |
2151,70 |
2255,30 |
1977,56 |
2141,44 |
2051,65 |
|
|
2267,02 |
1978,82 |
2043,45 |
2149,59 |
2041,94 |
2043,59 |
|
|
2042,44 |
2044,54 |
2037,73 |
2193,50 |
2266,04 |
2185,41 |
|
|
2191,74 |
1974,69 |
1977,43 |
2333,11 |
1975,34 |
2147,14 |
|
|
2427,21 |
1983,95 |
2046,58 |
1978,09 |
2042,71 |
2191,27 |
|
|
2187,23 |
2197,23 |
2298,93 |
2189,38 |
2057,13 |
2046,88 |
|
|
1978,33 |
2081,48 |
2290,99 |
2512,36 |
2188,47 |
1975,94 |
|
|
1975,80 |
1976,70 |
2190,03 |
2194,30 |
1976,64 |
2665,68 |
|
|
2141,42 |
2032,91 |
1975,21 |
2249,58 |
2041,50 |
1976,60 |
Table 2. Length of trajectory for 60% of accepted population
|
|
w1 |
w2 |
w3 |
w4 |
w5 |
w6 |
|
L [mm] |
2189,70 |
1975,43 |
1980,10 |
1976,64 |
1978,83 |
1975,56 |
|
1976,22 |
2040,13 |
2027,49 |
1978,35 |
2028,51 |
2195,18 |
|
|
1974,37 |
1982,43 |
2029,75 |
1981,49 |
2033,99 |
2525,41 |
|
|
2047,40 |
1976,10 |
2141,54 |
2043,92 |
2358,57 |
2059,93 |
|
|
2242,70 |
2062,55 |
1976,95 |
1974,45 |
1975,48 |
1977,22 |
|
|
1975,06 |
2010,17 |
1975,88 |
1977,76 |
1976,73 |
2188,88 |
|
|
1975,61 |
2043,25 |
1975,21 |
1976,97 |
1976,60 |
2201,67 |
|
|
1986,50 |
2264,59 |
2188,52 |
1974,87 |
2541,85 |
2194,03 |
|
|
2336,88 |
2190,35 |
2188,52 |
2063,96 |
1974,80 |
2044,47 |
|
|
1974,75 |
2044,91 |
2317,06 |
2196,02 |
1978,65 |
2188,90 |
Table 3. Length of trajectory for 100% of accepted population
|
|
w1 |
w2 |
w3 |
w4 |
w5 |
w6 |
|
L [mm] |
1983,07 |
2039,97 |
1983,12 |
1981,22 |
1982,92 |
1983,93 |
|
1978,31 |
2243,99 |
1983,83 |
1981,20 |
1984,99 |
1978,80 |
|
|
1979,83 |
2441,41 |
1983,99 |
1984,57 |
1980,19 |
1983,40 |
|
|
1982,61 |
1985,52 |
1982,29 |
1982,61 |
2240,56 |
1984,00 |
|
|
1986,93 |
1984,71 |
1983,96 |
2009,57 |
1983,67 |
1981,89 |
|
|
1981,48 |
2912,43 |
2242,48 |
1983,62 |
1983,14 |
1984,76 |
|
|
1982,94 |
2197,19 |
2225,60 |
1982,78 |
1982,55 |
1978,54 |
|
|
1988,51 |
1986,93 |
2220,23 |
1983,41 |
1974,75 |
2013,83 |
|
|
1983,83 |
1992,81 |
1977,02 |
2021,78 |
1975,50 |
1979,43 |
|
|
1985,19 |
2087,65 |
1979,09 |
1982,90 |
1986,73 |
1976,91 |
In the presented results (Tables 1-3), the PSO algorithm finds the shortest trajectory in the range [1974; 1985], this discrepancy is due to an insufficient number of iterations.
In the assumed population, 20% the shortest trajectory is found for the second weight (w2) L = 1974.69 mm, for this inertia weight half of the sought trajectory can be considered as the shortest. In the case of the other inertia weights, they have two of the shortest trajectories, and for w1 there are three trajectories.
In the case of 60% of the population, the shortest trajectory is for the first inertia weight (w1) L = 1974.37 mm. Furthermore for that inertia weight, half of the sought trajectories are the best solutions. Weights w4 and w5 are characterized by the largest number of shortest found trajectories, because they have 7 and 6 of these trajectories respectively.
The algorithm (for the results shown in Table 3) could not find a global minimum due to the fact that the entire population has reached the same trajectory almost at the beginning of the algorithm's operation. This is the result of the adoption of 149 populations (n = 100%) and one population connecting the starting point with the ending point (straight segment) - no drawing of intermediate points for the population in the first iteration.
Figure 5 shows the shortest found trajectory (n = 60%, w1).
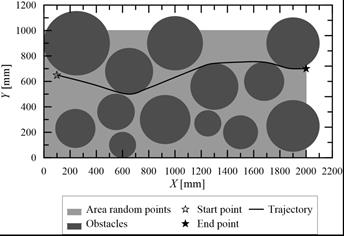
Fig. 5. The shortest found trajectory
4. Conclusions
The results obtained in this work can be useful in the selection of the inertia weight in the Particle Swarm Optimization algorithm. The inertia weight has a significant impact on the results of calculations. The use of the PSO method allows one to determine the optimal new trajectory or to correct an existing path in any working space with obstacles.
In the case of searching for a completely new trajectory, the first population should be avoided by providing the coordinates of the auxiliary points, which should be generated randomly.
However, when it is only necessary to correct the trajectory (e.g. positions of obstacle or their size have been changed), we can avoid drawing of the points and introducing their coordinates independently into the algorithm. In addition, an appropriate number of constant population (ideally within n = 60%) should be adopted based on the existing trajectory. In the variants n = 20% and n = 100%, the algorithm has too little or too many imposed population, so it does not improve the existing trajectory, it only looks for a new one or makes changes but to a small extent.
In algorithms in which weight factors are used, a number of tests should always be carried out before the final research to select the parameters of algorithm and applied weights.
In future studies, the authors plan to use obstacles with the irregular shape.
References
[1] Kennedy, J., & Eberhart, R.C. (1995). Particle Swarm Optimization. Proceedings of the IEEE International Conference on Neutral Networks, Volume 4, 1942-1948.
[2] Bai, Q. (2010). Analysis of particle swarm optimization algorithm. Computer and Information Science, 3, 1, 180-184.
[3] Tarnowski, W. (2011). Optymalizacja i polioptymalizacja w technice. Koszalin: Wydawnictwo Uczelniane Politechniki Koszalińskiej.
[4] Clerc, M., & Kennedy, J. (2002). The particle swarm-explosion, stability and convergence in a multidimensional complex space. IEEE Transaction on Evolutionary Computation, 6, 2, 58-73.
[5] Cheng, R., & Yao, M. (2001). Particle Swarm Optimizer with time-varying parameters based on a Novel Operator. Applied Mathematics & Information Sciences, 5, 2, 33-38.
[6] Szczepanik, M. (2013). Algorytmy rojowe w optymalizacji układów mechanicznych. Gliwice: Wydawnictwo Politechniki Śląskiej.
[7] Cekus, D., & Skrobek, D. (2016). Trajectory optimization of a SCARA manipulator using Particle Swarm Optimization. Machine Dynamics Research, 40, 1, 45-52.
[8] Cekus, D., & Waryś, P. (2015). Identification of parameters of discrete-continuous models. AIP Conf. Proc. 1648, 850055, DOI: 10.1063/1.4913110.
[9] Skrobek, D., & Cekus, D. (2019). Optimization of the operation of the anthropomorphic manipulator in a three-dimensional working space. Engineering Optimization, DOI: 10.1080/0305215X.2018.1564919.
[10] Ao, Y., & Chi, H. (2010). An adaptive differential evolution to solve constrained optimization problem in engineering design. Engineering, 2, 65-77.
[11] Lin, W., Lee, W., & Hong, T. (2003). Adapting crossover and mutation rates in genetic algorithms. Journal of Information Science and Engineering, 19, 889-903.
[12] Bansal, J.C., Singh, P.K., Saraswat, M., Verma, A., Jadon, S.S., & Abraham, A. (2011). Interia weight strategies in particle swarm optimization. Third World Congress on Nature and Biologically Inspired Computing (NaBIC), IEEE, 640-647, DOI: 10.1109/NaBIC.2011.6089659.
[13] Ting, T.O., Shi, Y., Cheng, S., & Lee, S. (2012). Exponential Inertia Weight for Particle Swarm Optimization. Advances in Swarm Intelligence, vol. 7331, Berlin, Heidelberg: Springer. DOI: 10.1007/978-3-642-30976-2_10.

