Strength statistical characteristics of the isotropic materials with disc-shaped defects
Roman Kvit
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
STRENGTH STATISTICAL CHARACTERISTICS OF THE ISOTROPIC MATERIALS WITH DISC-SHAPED DEFECTS
Roman Kvit
Lviv Polytechnic National University
Lviv, Ukraine
kvit_rom@ukr.net
Received: 24 October 2018; Accepted: 20 January 2019
Abstract. The expressions of the probabilities density distribution of failure loading for an elastic isotropic body under the action of a homogeneous axisymmetric loading are written. The disc-shaped cracks that do not interact with each other are uniformly distributed. The correlation for finding the most probable, mean value, dispersion and variation coefficient of failure loading are obtained. The dependence of the mentioned statistical strength characteristics on the type of applied loading, number of defects (body sizes) and structure material heterogeneity are investigated.
MSC 2010: 74R10, 74R99, 60K35, 82C03
Keywords: isotropic material, disc-shaped crack, distribution law, failure loading, strength statistical characteristics, axisymmetric loading
1. Introduction
The development of the strength theory and criteria of structural materials failure is an important and actual task. Wide application of high-strength materials, which are characterized by brittle fracture, necessitates the creation of reliable methods for predicting the properties of structural elements in the process of exploitation. For effective simulation of brittle materials fracture, it is important to take into account the stochastic nature of their structure. The complex application of known deterministic fracture mechanics solutions and probabilistic statistical methods enables us to construct qualitative models of structural elements strength and reliability for different types of loading. Such a technique has been developed in the articles [1-6].
The purpose of this study is to develop a method for calculating the statistical strength characteristics of brittle model materials under the conditions of homogeneous axisymmetric loading on the basis of defects deterministic theory and proba- bility theory methods.
2. Formulation of the problem
Studying the brittle materials fracture process, the consideration of the
defects such as cracks spatial location in a three-dimensional body is important.
The simplest model of a three-dimensional body with stochastically distributed
defects is
a flat, circular-planar (disc-shaped)
crack that is characterized by a radius ![]() and
two independent orientation angles in space. The
model is considerably simplified in the case of an axisymmetric loading. Then,
a disc-shaped crack in an axisymmetric
stress field is characterized by two statistically independent parameters:
the radius
and
two independent orientation angles in space. The
model is considerably simplified in the case of an axisymmetric loading. Then,
a disc-shaped crack in an axisymmetric
stress field is characterized by two statistically independent parameters:
the radius ![]() and the
orientation angle
and the
orientation angle ![]() between
the normal
between
the normal ![]() to the crack plane and the symmetry
axis
to the crack plane and the symmetry
axis ![]() .
.
We shall consider an elastic isotropic body
(or its element) that has volume ![]() , and is under the
conditions of a homogeneous axisymmetric loading
, and is under the
conditions of a homogeneous axisymmetric loading ![]() and
and ![]() . It evenly distributes
. It evenly distributes ![]() disc-shaped cracks that do not interact
with each other (the number
disc-shaped cracks that do not interact
with each other (the number ![]() will be assumed to
be proportional to volume
will be assumed to
be proportional to volume ![]() :
: ![]() , where
, where ![]() is
the number of defects per unit volume). The crack resistance of the material
is
the number of defects per unit volume). The crack resistance of the material ![]() will be considered the same throughout
the body.
will be considered the same throughout
the body.
In the case of
material isotropy, all the cracks orientations are equally probable
![]() . Therefore, the end of the normal
. Therefore, the end of the normal ![]() with the same probability covers the
area of the hemisphere
with the same probability covers the
area of the hemisphere ![]() . The
ends of the normal with orientation angles
. The
ends of the normal with orientation angles ![]() that
do not exceed a given value
that
do not exceed a given value ![]() , cover
the area of the spherical segment
, cover
the area of the spherical segment ![]() . The probability that the crack orientation angle
. The probability that the crack orientation angle ![]() will
not exceed a given value
will
not exceed a given value ![]() is defined as the ratio of the segment
areas and the hemisphere:
is defined as the ratio of the segment
areas and the hemisphere: ![]() [7].
Accordingly, the probability distribution density of
a random variable
[7].
Accordingly, the probability distribution density of
a random variable ![]() is written as
follows:
is written as
follows: ![]() .
.
We choose the probability distribution density of a random parameter ![]() in the form of a generalized b-distribution [8]:
in the form of a generalized b-distribution [8]: ![]()
![]() ,
, ![]() is
a finite structural characteristic). Then the distribution
function is defined as
follows:
is
a finite structural characteristic). Then the distribution
function is defined as
follows: ![]() . Here
. Here ![]() is the parameter of the material fracture (with
its
increasing the more probable are a small cracks).
is the parameter of the material fracture (with
its
increasing the more probable are a small cracks).
3. Distribution function of failure loading
In article [9] the expressions of the failure loading distribution function for a body element with one disc-shaped crack for the following loads are obtained:
1) all-round
tension for ![]()
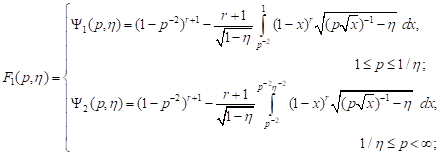 | (1) |
2) all-round
tension for ![]()
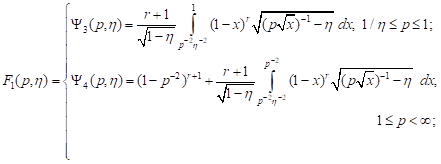 | (2) |
3) tension in the axial and compression in lateral
directions for ![]()
![]()
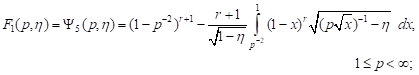 | (3) |
4) compression in the axial and tension in the lateral
directions for ![]()
![]()
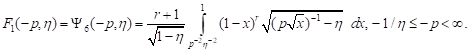 | (4) |
In the
expressions (1)-(4) immeasurable loading ![]() is introduced.
is introduced.
On the basis of the failure loading distribution function (1)-(4), the statistical strength characteristics of the axisymmetric loaded body (or its element) are determined.
Consider
partial cases: the same all-round tension (![]() ,
, ![]() ), biaxial tension (
), biaxial tension (![]() ,
, ![]() ,
, ![]() ), uniaxial tension (
), uniaxial tension (![]() ,
, ![]() ,
, ![]() ), tension in
the axial and equal to it compression in lateral directions (
), tension in
the axial and equal to it compression in lateral directions (![]() ,
, ![]() ) and compression in the axial and equal to it tension in the
lateral directions (
) and compression in the axial and equal to it tension in the
lateral directions (![]() ,
, ![]() ).
).
Then, the failure loading distribution function for element of the body with one crack will be written as follows:
1) for the same all-round tension
| (5) |
2) for biaxial tension
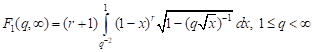 ; ; | (6) |
3) for uniaxial tension
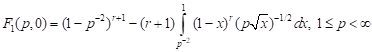 ; ; | (7) |
4) for tension in the axial and equal to it compression in lateral directions
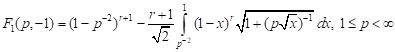 ; ; | (8) |
5) for compression in the axial and equal to it tension in the lateral directions
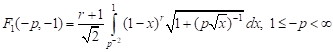 . . | (9) |
4. Distribution density probabilities of failure loading
For a body with a stochastic distribution of ![]() defects, the distribution density probabilities of failure loading are determined [8] as
follows:
defects, the distribution density probabilities of failure loading are determined [8] as
follows:
| (10) |
Substituting the expressions of the distribution function (1)-(4) into the formula (10), we obtain the expressions of the distribution density probabilities of fracture loading for a body with randomly distributed disc-shaped defect-cracks for the following cases of axisymmetric loading:
1) all-round
tension for ![]()
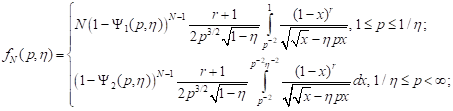 | (11) |
2) all-round tension for ![]()
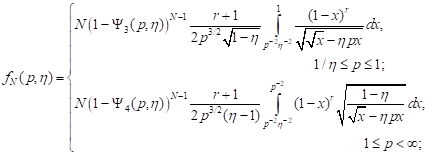 | (12) |
3) tension in the axial and compression in
lateral directions for ![]()
![]()
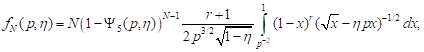
| (13) |
4) compression in the axial and tension in
the lateral directions for ![]()
![]()
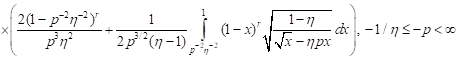 . . | (14) |
For partial cases, the distribution density probabilities of failure loading will be written as follows:
1) for the same all-round tension
| (15) |
2) for biaxial tension
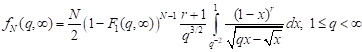 ; ; | (16) |
3) for uniaxial tension
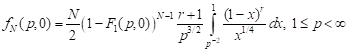 ; ; | (17) |
4) for tension in the axial and compression in lateral directions that is equal to it
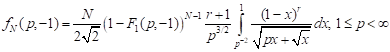 ; ; | (18) |
5) for compression in the axial and tension in lateral directions that is equal to it
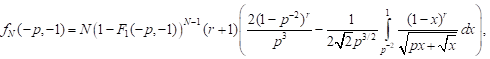 | (19) |
5. Probabilistic characteristics of failure loading
We will investigate some probabilistic characteristics of failure loading. Its most probable value (mode), which corresponds to the loading level, in which the distribution density probabilities reach a maximum, is determined from the equation [8]
| (20) |
Equation (20) can be reduced to a form
| (21) |
Mean value of fracture loading is written as follows [8]:
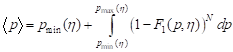 . . | (22) |
The dispersion and the coefficient of failure loading variation are found by the formulas [8]
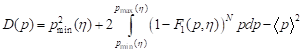 , , | (23) |
| (24) |
Substituting in formulas (20)-(24) the expressions for the failure
loading distribution function ![]() (1)-(9), we
obtain the relations for determination of the probability
strength characteristics considered.
(1)-(9), we
obtain the relations for determination of the probability
strength characteristics considered.
According to the expressions (15)-(19) in Figures 1 and 2 the graphs of
the distribution density
probabilities of failure loading ![]() for a body with stochastic
distribution of
for a body with stochastic
distribution of ![]() cracks for different types of a stressed state were
constructed. Distributions of a failure loading random variable will be unimodal. The threshold value of strength
not equal to zero and depends on the type of
loading.
cracks for different types of a stressed state were
constructed. Distributions of a failure loading random variable will be unimodal. The threshold value of strength
not equal to zero and depends on the type of
loading.
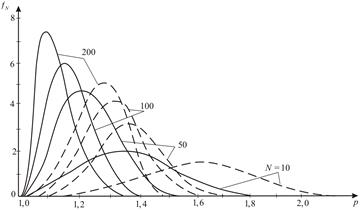
Fig. 1. Distribution density probabilities of
failure loading for the same
all-round tension for materials with different number of defects and
heterogeneity
(solid for ![]() , dashed for
, dashed for ![]() )
)
According to the expressions (22)-(24) in Figures 3-5, the graphs of failure loading probability characteristics for various types of stressed state for materials with different number of defects and different heterogeneity were constructed.
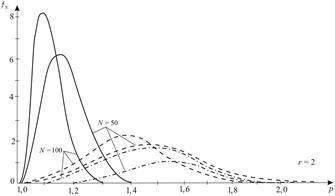
Fig. 2. Distribution density
probabilities of failure loading for various types of stressed state
(solid for ![]() , dashed for
, dashed for ![]() ,
dotted dashed for
,
dotted dashed for ![]() )
)
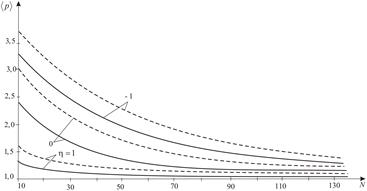
Fig. 3. The failure loading mean
value for various types of stressed state
(solid for ![]() , dashed for
, dashed for ![]() )
)
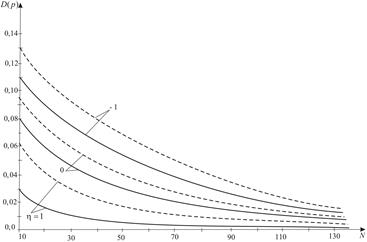
Fig. 4.
Dispersion of failure loading for various types of stressed state
(solid for ![]() , dashed for
, dashed for ![]() )
)
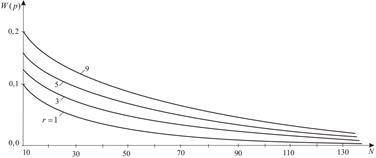
Fig. 5. Coefficient of failure loading variation for materials of different heterogeneity for the same all-round tension
6. Conclusions
In Figures 1 and 2, the influence of cracks
number ![]() in the body (body volume at the same
defect density), the distribution law of the cracks radiuses, that is, the
heterogeneity of the material (parameter
in the body (body volume at the same
defect density), the distribution law of the cracks radiuses, that is, the
heterogeneity of the material (parameter ![]() ) and
the ratio of the applied loading
(parameter
) and
the ratio of the applied loading
(parameter ![]() ) to the most probable value of strength (mode
) to the most probable value of strength (mode ![]() ) are considered.
) are considered.
As can be
seen from Figure 1, for the same all-round tension (![]() ), with the increasing in the number of cracks in the body,
decreases the most probable strength value. This tendency persists when
changing material heterogeneity
(parameter
), with the increasing in the number of cracks in the body,
decreases the most probable strength value. This tendency persists when
changing material heterogeneity
(parameter ![]() ). Increasing the value
). Increasing the value ![]() (increasing the uniformity of the
material) leads to an increase
(increasing the uniformity of the
material) leads to an increase ![]() . With the change of the parameter
. With the change of the parameter ![]() , the shape of the distribution density curve changes. The value
, the shape of the distribution density curve changes. The value ![]() can also be obtained from equation (21).
can also be obtained from equation (21).
In Figure 2, we see
a loading type influence on the body strength. The smallest value ![]() is observed for the same
all-round tension (
is observed for the same
all-round tension (![]() ), the greatest for tension in the axial and
equal to it compression in lateral directions (
), the greatest for tension in the axial and
equal to it compression in lateral directions (![]() ).
Similar conclusions are made in [10], where the indicated values
).
Similar conclusions are made in [10], where the indicated values ![]() are found
in another way. The magnitude
are found
in another way. The magnitude ![]() increasing and shape of the distribution density curve ares affected by the number of defects N.
increasing and shape of the distribution density curve ares affected by the number of defects N.
We note that the maximum ordinates of the
distribution curve are directly proportional to ![]() and
inversely proportional to r. This
feature does not depend on the type of applied loading. Consequently, in the
case of
and
inversely proportional to r. This
feature does not depend on the type of applied loading. Consequently, in the
case of ![]() increasing, the maximum value of the
distribution density also increases and decreases with
increasing, the maximum value of the
distribution density also increases and decreases with ![]() increasing.
increasing.
In Figure 3, the influence of the loading
ratio, the number of cracks and material homogeneity on the failure loading mean value ![]() is considered. With material homogeneity increasing,
the failure loading mean value increases. Its greatest value will be in case of
tension in the axial and equal to it compression in lateral directions. Such
regularities are observed in [9]. Note that there is a certain range of body
sizes, for which strength with an asymptotic approximation to its threshold
value almost does not depend on the defects number.
is considered. With material homogeneity increasing,
the failure loading mean value increases. Its greatest value will be in case of
tension in the axial and equal to it compression in lateral directions. Such
regularities are observed in [9]. Note that there is a certain range of body
sizes, for which strength with an asymptotic approximation to its threshold
value almost does not depend on the defects number.
Figure 4 shows the dependence of the
failure loading dispersion ![]() on the number of cracks, the
loading ratio and the material homogeneity. The dispersion is a decreasing function
of the number of cracks in the body. At a certain interval of
on the number of cracks, the
loading ratio and the material homogeneity. The dispersion is a decreasing function
of the number of cracks in the body. At a certain interval of ![]() change we see a rapid decreasing of
change we see a rapid decreasing of ![]() value. The nature of this decreas-
ing does not depend on the type of loading and parameter r. With a change in the parameter r, the strength dispersion varies in size, which is almost
independent
of
value. The nature of this decreas-
ing does not depend on the type of loading and parameter r. With a change in the parameter r, the strength dispersion varies in size, which is almost
independent
of ![]() . As in the case of the mean value
. As in the case of the mean value ![]() , there is a certain range of body sizes, for which the strength
dispersion is almost independent of the defects number.
, there is a certain range of body sizes, for which the strength
dispersion is almost independent of the defects number.
In Figure 5, the influence of material
homogeneity and the number of cracks on the coefficient of failure loading variation ![]() for the same all-round tension is investigated. The magnitude
for the same all-round tension is investigated. The magnitude ![]() increases with the parameter
increases with the parameter ![]() increasing and decreases with the cracks number
increasing and decreases with the cracks number ![]() increasing. There is a certain range of body sizes for which
we observe a significant change in the
increasing. There is a certain range of body sizes for which
we observe a significant change in the ![]() magnitude and
an asymptotic approximation to a certain threshold value. Similar
patterns are traced to other types of a stressed state.
magnitude and
an asymptotic approximation to a certain threshold value. Similar
patterns are traced to other types of a stressed state.
References
[1] Bazant, Z.P., Le, J.-L., & Yu, Q. (2010). Statistical aspects of quasibrittle size effect and lifetime with consequences for safety and durability large structures. Proceedings of FraMCoS-7, 1-8.
[2] Keles, Ö., Garcia, R., & Bowman, K. (2013). Stochastic failure of isotropic, brittle materials with uniform porosity. Acta Materialia, 61(8), 2853-2862.
[3] Bertalan, Z., Shekhawat, A., Sethna, J., & Zapperi, S. (2014). Fracture strength: stress concentration, extreme value statistics, and the fate of the Weibull distribution. Physical Review, 2,3, 034008.
[4] Heckmann, K., & Saifi, Q. (2016). Comparative analysis of deterministic and probabilistic fracture mechanical assessment tools. Kerntechnik, 81(5), 484-497.
[5] Wen, L., & Bazant, Z.P. (2017). Fishnet statistics for probabilistic strength and scaling of nacreous imbricated lamellar materials. Journal of the Mechanics and Physics of Solids, 109, 264-287.
[6] Zhang, T., Yue, R., Wang, X., & Hao, Z. (2018). Failure probability analysis and design comparison of multi-layered sic-based fuel cladding in PWRs. Nuclear Engineering and Design, 330, 463-479.
[7] Vytvytsky, P. (1989). Determination of failure probability at axisymmetric stressed state of the body with internal disc-shaped cracks. Physicochemical Mechanics of Materials, 6, 50-57 (in Ukrainian).
[8] Vytvytsky, P., & Popina, S. (1980). Strength and criteria of brittle fracture of stochastically defective bodies. Kyiv; 186 (in Russian).
[9] Vytvytsky, P., & Kvit, R. (1990). Probabilistic strength criteria for bodies with stochastically distributed disc-shaped cracks under an axisymmetric stress state. Physicochemical Mechanics of Materials, 3, 53-58 (in Ukrainian).
[10] Fisher, J., & Hollomon, J. (1947). A statistical theory of fracture. Metals Technology, 14(5), 1-16.

