Implicit scheme of the finite difference method for 1D dual-phase lag equation
Ewa Majchrzak
,Bohdan Mochnacki
Journal of Applied Mathematics and Computational Mechanics |
 Download Full Text |
IMPLICIT SCHEME OF THE FINITE DIFFERENCE METHOD FOR 1D DUAL-PHASE LAG EQUATION
Ewa Majchrzak1, Bohdan Mochnacki2
1Silesian
University of Technology
Gliwice, Poland
2University of Occupational Safety
Management in Katowice
Katowice, Poland
ewa.majchrzak@polsl.pl, bmochnacki@wszop.edu.pl
Received: 22 June 2017; Accepted: 5 September 2017
Abstract. The 1D dual-phase lag equation (DPLE) is solved using the implicit FDM scheme. The dual phase lag equation is the hyperbolic PDE and contains a second order time derivative and higher order mixed derivative in both time and space. The DPLE results from the generalization of the well known Fourier law in which the delay times are taken into account. So, in the equation discussed, two positive parameters appear. They correspond to the relaxation time τq and the thermalization time τT. The DPLE finds, among others, the application as the mathematical description of the thermal processes proceeding in the micro-scale. In the paper, the numerical solution of DPLE based on the implicit scheme of the FDM is presented. The authors show that a such an approach in the case of DPLE leads to the unconditionally stable differential scheme.
MSC 2010: 80M20, 80A20
Keywords: micro-scale heat conduction, dual-phase lag equation, finite difference method, stability of FDM implicit scheme
1. Introduction
Most typical problems in the field of transient heat conduction proceeding in the macro-scale are sufficiently good described by the well-known Fourier equation (energy equation). The considerations leading to this equation are based on the Fourier law in the form
| (1) |
where q is a
heat flux vector, λ is a thermal conductivity, ![]() is a temperature gradient. The
dual-phase lag model is based on the generalized form of the Fourier law,
namely [1, 2]
is a temperature gradient. The
dual-phase lag model is based on the generalized form of the Fourier law,
namely [1, 2]
| (2) |
where τq is the relaxation time and τT is the thermalization time. In the case of metals, both the relaxation and thermalization times are very small and, considering the macro-scale problems, they may be omitted (as in formula (1)). Another situation takes place for the micro-scale heat conduction problems.
When the characteristic length of the domain is comparable to or smaller than the mean free path of heat carriers or the duration of the process is comparable to or less than the relaxation time of the heat carriers, then the Fourier equation leads to erroneous results [3] and the DPL model should be taken into account.
The dual phase lag equation can be written in the form [1-4]
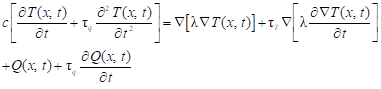 | (3) |
where c is a volumetric specific heat and Q is a capacity of internal volumetric heat sources. The equation (3) must be supplemented by the appropriate boundary and initial conditions.
The aim of the considerations presented in this paper is the application of the implicit FDM scheme for the approximate solution of the micro-scale 1D problem (heating of thin metal film) taking into account the presence of internal heat sources. The stability of the differential scheme is also discussed. In the final part of the paper, the example of numerical computations is also shown.
2. Formulation of the problem
Temperature field T(x, t) in the thin metal film (layer thickness is equal to L) subjected to the laser action is described here by the dual-phase lag equation in the form
| (4) |
where a = λ/c is a thermal diffusivity. The laser action can be taken into account by the introduction of internal source function defined as follows [4, 5]
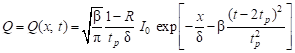 | (5) |
where I0 is the laser intensity, tp is the characteristic time of a laser pulse, δ is the absorption depth, R is the reflectivity of the irradiated surface and β = 4 ln2.
Introduction of an artificial heat source to the mathematical model of laser heating allows one to assume the no-flux boundary conditions on the surfaces limiting the domain considered
| (6) |
The initial conditions are also known, meaning
| (7) |
where Tp is the initial temperature of thin film and w(x) is the initial heating rate.
3. Implicit scheme of the finite difference method
The following approximate form of equation (4) is proposed
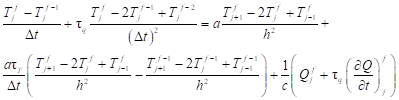 | (8) |
where h is the grid step and ∆t is the time step, j is the index of the central point of star, f − 2, f − 1, f denotes the successive time levels. The equation (8) can be written in the form
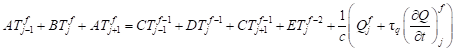 (9) (9) |
where
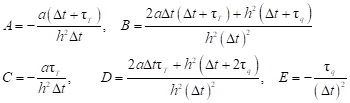 | (10) |
In the case of boundary nodes, the following dependence (corresponding to the Neumann boundary condition) should be taken into account [6]
| (11) |
Thus, for the boundary node 0 one has (c.f. equation (6))
| (12) |
and then
| (13) |
while for the boundary node n
| (14) |
and then
| (15) |
The system of equations (9), (13), (15) written in the form
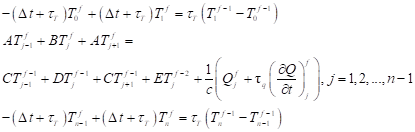 | (16) |
can be solved using the Thomas algorithm.
4. Stability of differential scheme
The approximation error carried by ![]() at every node of space j and time
f is assumed to have a wave form with the wave number denoted by k
and the amplitude by δ [1, 7]:
at every node of space j and time
f is assumed to have a wave form with the wave number denoted by k
and the amplitude by δ [1, 7]:
| (17) |
As time progresses,
to assure convergence, the amplitude of the approximation error must be less
than unity, i.e. ![]() .
.
Introducing the formula (17) into equation (9), one has (the source function is omitted here)
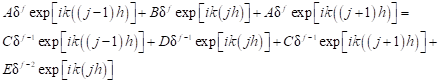 | (18) |
or
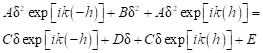 | (19) |
Using the Euler formulas, one obtains
| (20) |
or
| (21) |
where
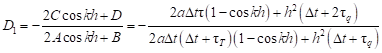 | (22) |
and
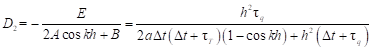 | (23) |
According to [8], the absolute values of the roots of equation (21) are less than 1 when
| (24) |
So
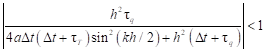 | (25) |
and
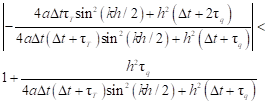 | (26) |
The inequality (25) should be substituted by two inequalities. The first of these is
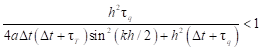 | (27) |
meaning
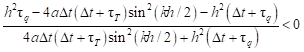 | (28) |
One can see that the denominator of the fraction (28) is positive. Simultaneously, the numerator should be negative and the least favorable situation corresponds to sin 2 (kh/2) = 0 and then
| (29) |
The result corresponds to the uncoditional inequality. The second condition resulting from (25) is of the form
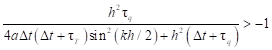 | (30) |
or
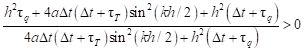 | (31) |
One can see that this condition is always fulfilled.
The inequality (26) can be written in the form
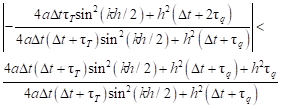 | (32) |
The first inequality resulting from (32) is of the form
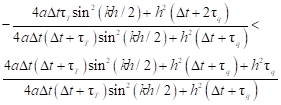 | (33) |
or (taking into account that the denominator of the fraction is positive)
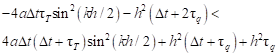 | (34) |
and next
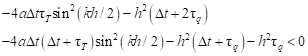 | (35) |
One can see that the above inequality is the uncoditional one.
The second condition resulting from (32) is the following
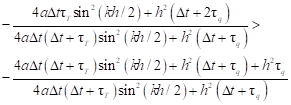 | (36) |
or (taking into account that the denominator of the fraction is positive)
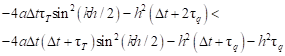 | (37) |
Finally
| (38) |
The condition (38) is unconditional.
Summing up, the implicit scheme of the finite difference method for the dual-phase lag equation is always stable.
5. Results of computations
The thin metal film (gold) of thickness 100 nm is considered. The initial temperature Tp = 20oC, the initial heating rate w(x) = 0. Thermophysical parameters of the film are the following: λ = 315 W/(mK), c = 2.4897 MJ/(m3 K), τq = 8.5 ps, τT = 90 ps. In the formula (5): R = 0.93, I0 = 13.4 J/m2, tp = 0.1 ps, δ = 15.3 nm. The mesh step h = 1 nm (n = 100), the time step ∆t = 0.0002 ps.
In Figure 1, the temperature histories at the selected points from the domain considered are shown, while Figure 2 illustrates the temperature profiles for times 0.2, 0.5, 1 and 3 ps. It should be noted that the results are practically the same as the analytical solution presented by Ciesielski in the paper [9].
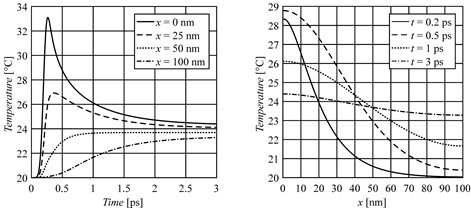
Fig. 1. Temperature histories at selected points Fig. 2. Temperature profiles for different times
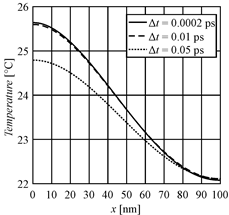
Fig. 3. Temperature profiles for t = 1.2 ps and different time steps
Figure 3 illustrates the numerical solutions obtained for the different time steps. The first temperature profile for t = 1.2 ps has been found for the very small time interval. The second profile corresponds to ∆t = 0.01 ps, while the last (significantly different from the previous) has been computed for ∆t = 0.05 ps. The time interval ∆t = 0.01 ps is longer than the critical one for the FDM explicit scheme [10]. In spite of this, the solution is of a good accuracy. In turn, from a qualitative point of view, the last solution is basically correct but inaccurate. In the case considered, the essential errors result from the fact that the source function Q is time-dependent and for the large time step its approximation is a bit unclear.
6. Conclusions
In the paper, the problem of the implicit FDM scheme for a numerical solution of DPLE is discussed. The authors present in detail the numerical algorithm for the 1D task. Analysis of the 1D numerical solution results from the fact that there is a possibility to compare the results with an analytical solution [9]. The generalization of the algorithm presented for 2D or 3D problems is quite simple here.
It should be pointed out that the implicit differential schemes are generally stable. Despite this, the stability problem has been analyzed in detail. In particular, the approach resulting from the von Neumann analysis application [1, 7] is presented. Such an approach leads to the conditions (inequalities) determining the critical value of ∆t. It was shown that the all inequalities limiting this value are unconditional.
In the case of the task under consideration, the time step can be significantly increased compared to the explicit FDM scheme. Unfortunately, too much of a time step leads to the incorrect numerical results (as shown in Figure 3). The test calculations were also carried out in the case of the Dirichlet condition given for x = 0 under the assumption that Q = 0. In this type of problem, the time step can be significantly extended in comparison to ∆t corresponding to the Neumann boundary conditions.
It should be noted that the stability for the three-level scheme presented here can be also analyzed using the different approaches e.g. [11, 12].
Acknowledgement
This work is supported by the project No. 2015/19/B/ST8/01101 and sponsored by the National Science Centre (Poland).
References
[1] Tzou D.Y., Macro- to Microscale Heat Transfer: The Lagging Behavior, John Wiley & Sons, Ltd 2015.
[2] Zhang Z.M., Nano/Microscale Heat Transfer, McGraw-Hill, New York 2007.
[3] Escobar R.A., Ghai S.S., Jhon M.S., Amon C.H., Multi-length and time scale thermal transport using the lattice Boltzmann method with application to electronic cooling, International Journal of Heat and Mass Transfer 2006, 49, 97-107.
[4] Majchrzak E., Mochnacki B., Suchy J.S., Numerical simulation of thermal processes proceeding in a multi-layered film subjected to ultrafast laser heating, Journal of Theoretical and Applied Mechanics 2009, 47, 2, 383-396.
[5] Al-Nimr M.A., Heat transfer mechanism during short duration laser heating in thin metal films, International Journal of Thermophysics 1997, 18(5), 1257-1268.
[6] Majchrzak E., Mochnacki B., Sensitivity analysis of transient temperature field in microdomains with respect to the dual phase lag model parameters, International Journal for Multiscale Computational Engineering 2014, 12(1), 65-77.
[7] McDonough J.M., Kunadian I., Kumar R.R., Yang T., An alternative discretization and solution procedure for the dual phase-lag equation, Journal of Computational Physics 2006, 219, 163-171.
[8] Young D.M., Iterative Solution of Large Linear Systems, Academic Press, New York 1971.
[9] Ciesielski M., Analytical solution of the dual phase lag equation describing the laser heating of thin metal film, Journal of Applied Mathematics and Computational Mechanics, 2017, 16(1), 33-40.
[10] Majchrzak E., Mochnacki B., Dual-phase lag equation. Stability conditions of a numerical algorithm based on the explicit scheme of the finite difference method, Journal of Applied Mathematics and Computational Mechanics 2016, 15(3), 89-96.
[11] Castro M.A., Martin J.A., Rodriguez F., Unconditional stability of a numerical method for the dual-phase-lag equation, Mathematical Problems in Engineering 2017, 5 pages.
[12] Kaba I.K., Dai W., A stable three-level finite difference scheme for solving the parabolic two-step model in a 3D micro-sphere heated by ultrashort-pulsed lasers, Journal of Computational and Applied Mathematics 2005, 181, 125-147.

